Диаскопическая система первого вида

Существует два вида диапроекции:

1. Источник света проектируется на входной зрачок объектива. Применяется, в случае, когда источник света имеет неравномерную яркость.
2. Источник света проектируется на диапозитив. Применяется в случае, когда источник света имеет равномерную яркость.

Рассмотрим габаритный расчет диаскопической системы первого вида (рис. 3.1).

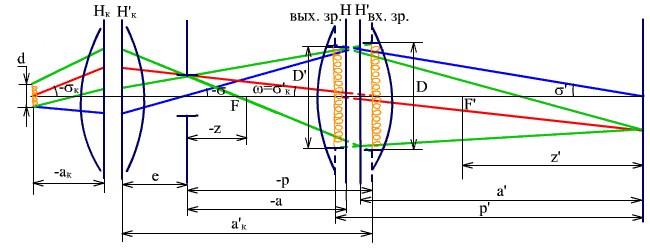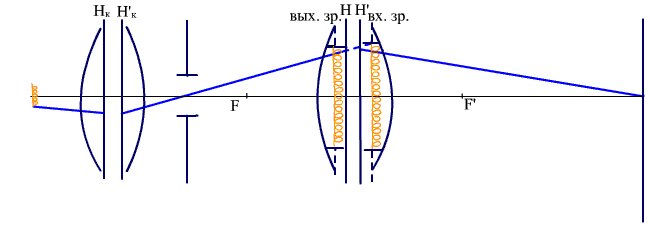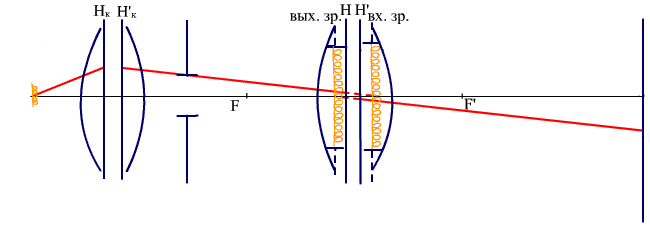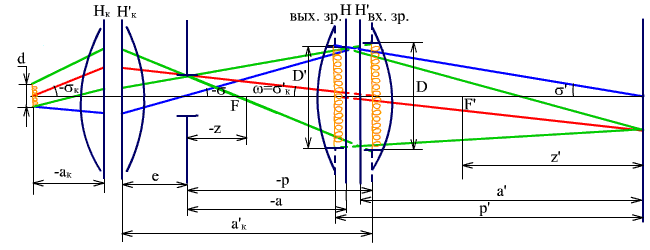
Рис. 3.1. Диаскопическая система. Источник света проектируется во входной зрачок объектива.

Линейное увеличение объектива равно:

,

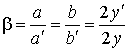где a, b - размеры сторон диапозитива, a', b' - размеры экрана, 2y, 2y' - диагонали диапозитива и экрана,

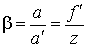, (3.2)

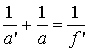. (3.3)

Применяя формулы (3.2) и (3.3), находим отрезок a, определяющий положение диапозитива относительно объектива и f' - фокусное расстояние объектива.

Для определения диаметра выходного зрачка воспользуемся известной формулой:

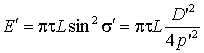. (3.4)

Диаметр выходного зрачка равен:

,

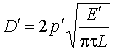где p' - расстояние от выходного зрачка до экрана, L - габаритная яркость выбранной лампы.

Если относительное отверстие объектива D' / f' получилось очень большое или очень маленькое нужно заменить лампу.

Из рис. 3.1 следует:

,

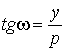где p - расстояние от входного зрачка до диапозитива.

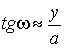. (3.5)

Поскольку тип объектива пока не известен, при предварительном расчете примем D' = D и p = a, тогда можно воспользоваться формулой (3.5) и определить угловое поле объектива.

Проекционные объективы должны обеспечивать:

 четкое изображение проецируемого предмета и правильную передачу контраста (исправляются все аберрации, кроме дисторсии, которая не должна превышать установленных границ);

 распределение освещенности на экране должно соответствовать распределению яркости на диапозитиве (не должно быть виньетирования).

В качестве проекционных объективов могут использоваться фотографические объективы. Если увеличения небольшие, то применяют и специально рассчитанные объективы.

Рассмотрим расчет осветительной части. Увеличение конденсора, проектирующего источник света во входной зрачок объектива, определяется по формуле (3.6):

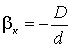, (3.6)

где D - диаметр входного зрачка объектива, d - размер меньшей стороны тела накаливания,

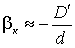, (3.7)

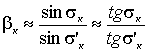. (3.8)

Для предварительного расчета можно воспользоваться формулами (3.7) и (3.8). Из рис. 3.1 следует: 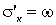. Тогда из формулы (3.8) получаем:

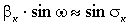, (3.9)

где σ_к - передний апертурный угол конденсора, который составляет половину угла охвата конденсора, от которого зависит сложность конструкции конденсора.

При предварительном расчете может получиться, что sin σ_к больше единицы, это значит нужно уменьшить β_к за счет увеличения размера тела накала. Если нет лампы с большим телом накаливания, можно для увеличения тела накала применить сферическое зеркало (рис. 3.2). В плоскости, проходящей через центр кривизны зеркала, помещается источник света, смещенный относительно оптической оси так, что в результате отражения от зеркала получается изображение источника, равное самому источнику, т.е. размер источника как бы удваивается. Угол охвата конденсора в соответствии с формулой (3.9) уменьшается приблизительно в два раза.

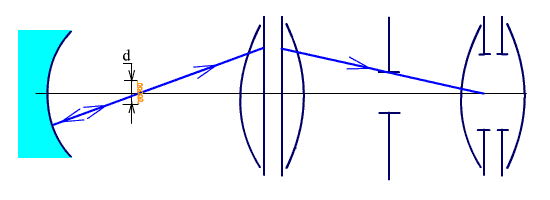
Рис. 3.2. Диаскопическая система с контротражателем.

Если источник света не смещать, то можно увеличить за счет отражения от зеркала габаритную яркость лампы почти в два раза (потери на отражение). Лампу несколько наклоняют, чтобы изображение нитей лампы получилось в интервале между нитями. Этот прием позволяет уменьшить относительное отверстие объектива.

После выбора объектива и типа конденсора производиться уточнение расчета.

Типы конденсоров

Конденсоры служат для равномерного освещения проецируемого предмета и бывают:

 линзовые;

 зеркальные;

 зеркально-линзовые;

 линзы Френеля.

Основными параметрами конденсоров являются: угол охвата σ_к и линейное увеличение β_к.

Конденсоры рассчитываются на минимум сферической аберрации, т.к. большие аберрации приводят к неравномерности освещения экрана.

Линзовые конденсоры в зависимости от угла охвата делятся на: однолинзовые, двухлинзовые, трехлинзовые и даже четырехлинзовые.

Однолинзовый конденсор (рис. 3.3) рассчитанный на минимум сферической аберрации имеет:

,

.

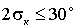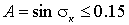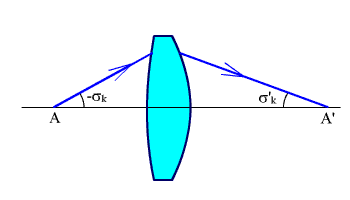
Рис. 3.3. Однолинзовый конденсор.

Двухлинзовый конденсор, состоящий из двух плосковыпуклых линз, показан на рис. 3.4.

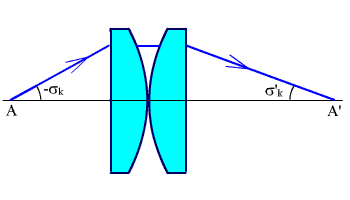
Рис. 3.4. Конденсор из двух плосковыпуклых линз.

,

,

.

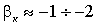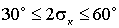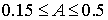Конденсор из апланатического мениска и линзы, рассчитанной на минимум сферической аберрации (рис. 3.5) имеет:

,

,

.

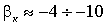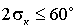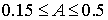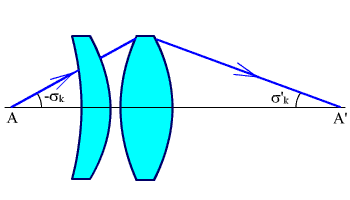
Рис. 3.5. Двухлинзовый конденсор с апланатическим мениском.

Если одна из поверхностей асферическая, то апертура может быть увеличена до 0,7.

Чем больше коэффициент дисперсии, тем меньше хроматизм, поэтому конденсор делают из кронов.

Трехлинзовый конденсор, рассчитанный на минимум сферической аберрации (рис. 3.6) имеет:

,

.

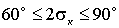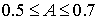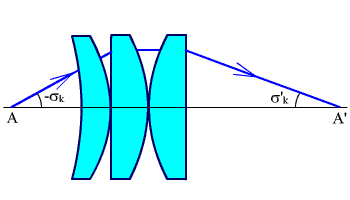
Рис. 3.6. Трёхлинзовый конденсор.

Пример зеркальной осветительной системы дан на рис. 3.7.

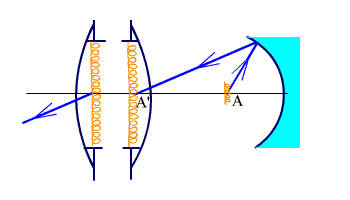
Рис. 3.7. Зеркальный конденсор.

Зеркальные системы имеют большой угол охвата и не имеют хроматизма. Простейшей зеркальной системой является сферическое зеркало, но чаще всего используется эллипсоидальное зеркало. Источник света располагается в одном из геометрических фокусов эллипса, а его изображение получается в другом фокусе. У эллипсоидальных отражателей угол охвата достигает 140°.

Пример зеркально-линзовой системы приведен на рис. 3.8.

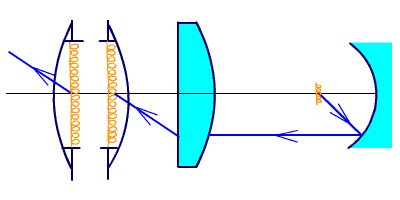
Рис. 3.8. Зеркально-линзовый конденсор.

Сложные многолинзовые конденсорные системы могут быть заменены линзами Френеля (рис. 2.77, рис. 2.79). Особенностью линз Френеля является большой угол охвата 2σ_к ≥ 100° и хорошее исправление сферической аберрации. 3.2.3. Расчет конденсора на минимум сферической аберрации.

Конденсор помещается между источником света и диапозитивом и непосредственно не участвует в образовании изображения на экране, поэтому необходимости в коррекции аберраций конденсора, казалось бы, нет. Однако, при наличии у конденсора большой сферической аберрации могут возникнуть два нежелательных явления:

 неравномерность освещенности в плоскости диапозитива, которая передается на экран;

 срезание пучков лучей апертурной диафрагмой и оправами линз, что приводит к потере световой энергии и вредному нагреванию оправы объектива.

Для коррекции сферической аберрации можно пойти по одному из двух путей:

 ввести в оптическую систему конденсора отрицательные линзы;

 применить асферическую поверхность.

Оба этих пути приводят к удорожанию конденсора и часто оказываются экономически неоправданными. В таком случае в конденсоре, состоящем только из положительных линз, минимизируется сферическая аберрация.

Рассмотрим расчет конденсора на минимум сферической аберрации. Для упрощения расчетов вначале будем считать все толщины линз равными нулю и все высоты нулевых лучей на поверхностях линз конденсора равными.

Расчет выполняется по формулам теории аберраций третьего порядка. Составляется выражение для сферической аберрации третьего порядка, берется первая производная по углам нулевого луча, приравнивается нулю, затем после преобразования получаются формулы для определения нечетных и четных углов конденсора.

Для нечетных углов:

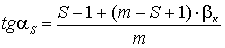, (3.10)

для четных углов:

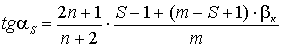, (3.11)

где m - число преломляющих поверхностей, S - номер поверхности.

Если конденсор однолинзовый, то получаются следующие расчетные формулы:

tg α₁ = β_к,

,

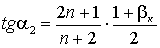tg α₃ = 1.

При расчетах по формулам (3.10), (3.11) всегда tg α₁ = β_к, а для последнего угла tg α_m+1 = 1.

Радиусы кривизны линз конденсора определяются по формуле:

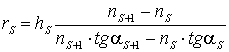, (3.12)

где n_s, n_s+1 - показатели преломления, а h_s - высота нулевого луча на главной плоскости поверхности.

На рис. 3.9 приведен двухлинзовый конденсор, для которого:

tg α₁ = β_к,

tg α_s+1 = tg α₅ = 1,

d₁ = d₂ = d₃ = 0,

.

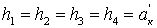Отрезок 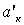и диаметр конденсора Ø известны из габаритного расчета проекционной системы.

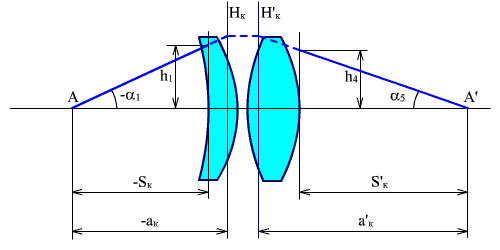
Рис. 3.9. Двухлинзовый конденсор.

После определения углов по формулам (3.10) и (3.11), находят радиусы по формуле (3.12) при нулевых толщинах линз, затем линзы вычерчиваются и определяются толщины линз, при этом должно быть выполнено условие (рис. 3.10):

4d + 10t = Ø_к

или толщина линзы по краю должна быть не меньше 0.05 ее диаметра.

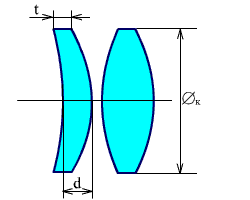
Рис. 3.10. Определение толщины линз.

После определения толщин линз уточняются высоты по формуле:

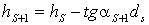, (3.13)

и производится пересчет радиусов по формуле (3.12). Затем определяются передний отрезок S_к и задний отрезок 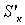по формулам:

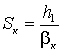, (3.14)

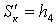. (3.15).