С неярко выраженной асимметрией торцов
И смещения центра масс вдоль продольной оси симметрии
На дне бункера БЗУ
Обозначим вероятности того, что предмет обработки ляжет на дно бункера асимметричным торцом, цилиндрическим торцом или боковой поверхностью соответственно как 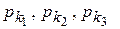 . Так как предмет обработки, брошенный на дно бункера, ляжет на него обязательно какой-либо из трех ограничивающих его поверхностей, то
. Так как предмет обработки, брошенный на дно бункера, ляжет на него обязательно какой-либо из трех ограничивающих его поверхностей, то
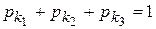 . (5)
. (5)
Переход предмета обработки в требуемое ориентированное положение III, в котором предмет обработки подходит к диску с захватывающими органами асимметричным торцом вперед, не возможен, если предмет обработки находится на дне бункера в положениях I, II. Тогда вероятность того, что предмет обработки ляжет на дно бункера поверхностью, при нахождении на которой возможен его переход в требуемое ориентированное положение, в соответствии с (5) будет равна
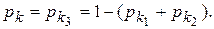 (6)
(6)
Выражения для определения вероятностей 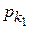 ,
, 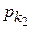 получены на основе известной методики следующим образом.
получены на основе известной методики следующим образом.
Вероятности перехода предмета обработки в первое определенное устойчивое положение выразим телесным углом 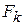 , соответствующим k-й поверхности предмета обработки и образуемым бесконечным количеством лучей выходящих из центра масс предмета обработки и пересекающих все точки периметра его k-й базисной поверхности. Так как мерой телесного угла принято считать площадь, вырезаемую этим углом на сфере единичного радиуса, а полный телесный угол равен
, соответствующим k-й поверхности предмета обработки и образуемым бесконечным количеством лучей выходящих из центра масс предмета обработки и пересекающих все точки периметра его k-й базисной поверхности. Так как мерой телесного угла принято считать площадь, вырезаемую этим углом на сфере единичного радиуса, а полный телесный угол равен 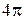 , то указанные вероятности будут выражены зависимостью
, то указанные вероятности будут выражены зависимостью
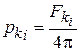 . (7)
. (7)
Телесные углы 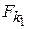 и
и 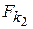 определяются соответственно по известным выражениям (рис. 3)
определяются соответственно по известным выражениям (рис. 3)
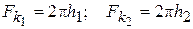 , (8)
, (8)
где 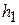 ,
, 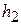 – высоты сегментов окружности, вырезаемых лучами на сфере единичного радиуса «1», проведенными из центра масс предмета обработки к цилиндрическому и коническому торцам соответственно и характеризуемыми центральными углами
– высоты сегментов окружности, вырезаемых лучами на сфере единичного радиуса «1», проведенными из центра масс предмета обработки к цилиндрическому и коническому торцам соответственно и характеризуемыми центральными углами 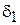 ,
, 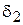 .
.
Из расчетной схемы (см. рис. 3) имеем
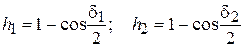 , (9)
, (9)
а косинусы половины центральных углов 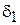 ,
, 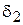 равны
равны
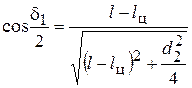 ;
; 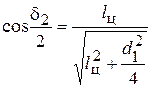 . (10)
. (10)
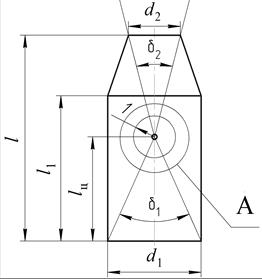
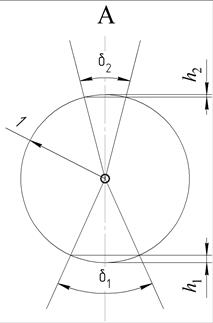
Рис. 3. Расчетная схема для определения вероятностей 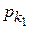 ,
, 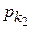
Подставляя выражения (8), (9), (10) в формулу (7), после несложных преобразований получим соответствующие зависимости для вероятностей 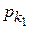 и
и 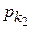 в виде
в виде
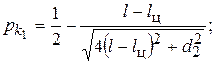
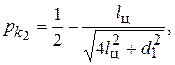 (11)
(11)
где 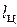 – расстояние от плоскости цилиндрического торца до центра масс предмета обработки (см. рис. 3).
– расстояние от плоскости цилиндрического торца до центра масс предмета обработки (см. рис. 3).
Тогда вероятность 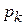 того, что предмет обработки ляжет на дно бункера поверхностью, при нахождении на которой возможен его переход в требуемое ориентированное положение, после подстановки зависимостей (11) в выражение (6) и перехода к безразмерным параметрам будет равна
того, что предмет обработки ляжет на дно бункера поверхностью, при нахождении на которой возможен его переход в требуемое ориентированное положение, после подстановки зависимостей (11) в выражение (6) и перехода к безразмерным параметрам будет равна
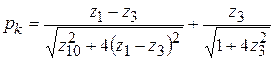 , (12)
, (12)
где 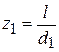 ;
; 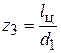 ;
; 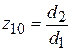 .
.
Вероятность 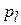 поворота предмета обработки требуемой поверхностью к захватывающему органу при отсутствии помех в осуществлении этого перехода определим, используя предельные значения этой вероятности [5]. Наибольшее значение
поворота предмета обработки требуемой поверхностью к захватывающему органу при отсутствии помех в осуществлении этого перехода определим, используя предельные значения этой вероятности [5]. Наибольшее значение 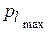 вероятность
вероятность 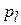 принимает на участке зоны захвата, свободном от предметов обработки
принимает на участке зоны захвата, свободном от предметов обработки
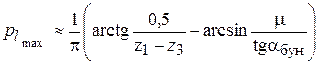 (13)
(13)
где μ – коэффициент трения скольжения предмета обработки о поверхности БЗУ; 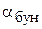 – угол наклона дна бункера зубчатого БЗУ к горизонту.
– угол наклона дна бункера зубчатого БЗУ к горизонту.
Минимальное значение 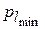 вероятности
вероятности 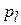 рассчитывают по формуле
рассчитывают по формуле
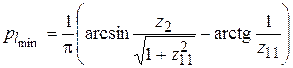 , (14)
, (14)
где 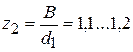 ; В – ширина захватывающего органа (
; В – ширина захватывающего органа ( 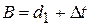 , см. рис. 1);
, см. рис. 1); 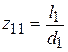 ;
; 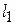 – длина цилиндрического торца предмета обработки (см. рис. 3).
– длина цилиндрического торца предмета обработки (см. рис. 3).
Тогда для определения вероятности 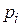 , входящей в выражение (4), используем выражение
, входящей в выражение (4), используем выражение
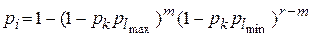 , (15)
, (15)
где т – показатель, зависящий от длины отрезка линии стыка, свободного от предметов обработки ( 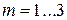 ); r – число предметов обработки, которое может одновременно поместиться в зоне захвата на периферии диска зубчатого БЗУ.
); r – число предметов обработки, которое может одновременно поместиться в зоне захвата на периферии диска зубчатого БЗУ.
В работе [3] было предложено новое определение числа предметов обработки, которое может одновременно поместиться в зоне захвата
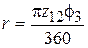 , (16)
, (16)
где 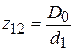 ; D0 – диаметр диска зубчатого БЗУ по оси расположения захватывающих органов (гнезд);
; D0 – диаметр диска зубчатого БЗУ по оси расположения захватывающих органов (гнезд); 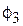 – угол, характеризующий зону захвата предметов обработки, на протяжении которого возможно западание предмета обработки в гнездо.
– угол, характеризующий зону захвата предметов обработки, на протяжении которого возможно западание предмета обработки в гнездо.
Величина угла 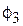 определена из анализа условий статического равновесия предмета обработки в радиальном пазу диска БЗУ с учетом угла наклона диска к горизонтали, коэффициента трения и геометрических размеров предмета обработки.
определена из анализа условий статического равновесия предмета обработки в радиальном пазу диска БЗУ с учетом угла наклона диска к горизонтали, коэффициента трения и геометрических размеров предмета обработки.
Тогда выражение (8) для вероятности захвата 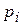 на основании полученных формул (12) –(16) запишется в виде
на основании полученных формул (12) –(16) запишется в виде
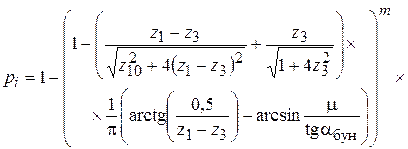
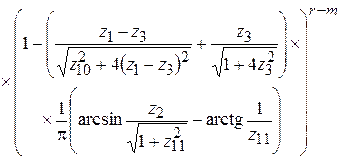 . (17)
. (17)
Вероятность того, что захвату предметов обработки гнездом не помешает взаимная сцепляемость предметов обработки, определится по известному выражению
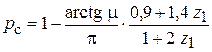 . (18)
. (18)
Известно, что при некотором предельном значении окружной скорости 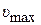 захватывающих органов производительность БЗУ падает до нуля. В этом случае из выражения (1) следует, что при этом значении окружной скорости нулю должен быть равен коэффициент выдачи η. Тогда в соответствии с выражением (3) получим
захватывающих органов производительность БЗУ падает до нуля. В этом случае из выражения (1) следует, что при этом значении окружной скорости нулю должен быть равен коэффициент выдачи η. Тогда в соответствии с выражением (3) получим
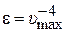 . (19)
. (19)
Предположим, что предельное значение окружной скорости 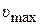 захватывающих органов, при котором производительность и коэффициент выдачи зубчатого БЗУ приближаются к нулевым значениям, соответствует ситуации, когда величина кинетической энергии, сообщенной предмету обработки движущимся диском с радиальными пазами при неупругом ударе предмета обработки о край паза, будет достаточна для выброса предмета обработки из паза. В этом случае ни один предмет обработки, находящийся на поверхности вращающегося диска с радиальными пазами, не сможет занять благоприятного положения в пазу для последующего западания в гнездо диска (рис. 4).
захватывающих органов, при котором производительность и коэффициент выдачи зубчатого БЗУ приближаются к нулевым значениям, соответствует ситуации, когда величина кинетической энергии, сообщенной предмету обработки движущимся диском с радиальными пазами при неупругом ударе предмета обработки о край паза, будет достаточна для выброса предмета обработки из паза. В этом случае ни один предмет обработки, находящийся на поверхности вращающегося диска с радиальными пазами, не сможет занять благоприятного положения в пазу для последующего западания в гнездо диска (рис. 4).
В этом случае удар кромки паза, движущегося с постоянной скоростью 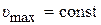 , приходится в боковую поверхность цилиндрической части предмета обработки, и он будет выброшен из паза при условии
, приходится в боковую поверхность цилиндрической части предмета обработки, и он будет выброшен из паза при условии
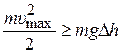 , (20)
, (20)
где m – масса предмета обработки; 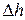 – глубина западания предмета обработки в радиальный паз.
– глубина западания предмета обработки в радиальный паз.
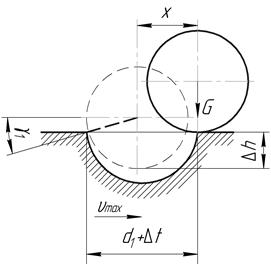
Рис. 4. Расчетная схема к определению предельной окружной скорости
Дата добавления: 2020-10-14; просмотров: 720;











