Указания к выполнению работы
Схему замещения сети в данном случае удобно представить в виде сопротивлений всех трех фаз трансформатора и линии так, как это показано на рис. 4.1б.
Проводимость линии и трансформатора в данном случае не учитывается, так как в низковольтных сетях она не оказывает заметного влияния на результаты расчетов.
Значения сопротивлений проводов линии 0,38 кВ и трансформатора набирают на горизонтальной панели стенда при помощи специальных проводников и перемычек. На стенде указаны марка, сечение, длина провода и мощность трансформатора.
Нагрузка также должна быть набрана на горизонтальной части панели стенда, маркировка ее дана в ваттах. Подсоединять нагрузку нужно параллельно сопротивлению линии.
Подобие модели реальной сети создается подбором масштабов МU, MI, Мz и МР.
Показания амперметра и вольтметра, а также результаты вычислений сводят в таблицу.
Контрольные вопросы
1. Вкаких случаях возникает несимметрия напряжения в сети?
2.Какие виды несимметричных нагрузок вызнаете?
3.В чем заключается сложность расчета сети с несимметричной нагрузкой?
4.Какое влияние оказывает несимметричная загрузка фаз на работу электрической сети?
5. Как уменьшить несимметрию в сети?
Раздел 3. МЕХАНИЧЕСКИЙ РАСЧЕТ ВОЗДУШНЫХ ЛИНИЙ
Механический расчет проводов
Расчет проводов на механическую прочность проводят для определения максимальной стрелы провеса и тяжения в проводе при наиболее неблагоприятных метеорологических условиях, которые могут возникнуть в районе проектируемой линии электропередачи, а также для составления монтажных таблиц, т.е. значений напряжения и тяжения в проводе и стрел провеса для различных температур окружающей среды.
Расчет делится на четыре этапа: определение удельных механических нагрузок, определение наиболее тяжелых расчетных условий, т.е. условий, при которых напряжение в проводе максимально, определение максимальной стрелы провеса и составление монтажной таблицы.
Задача 3.1
Провести механический расчет проводов АС70 для воздушной линии 10 кВ, сооружаемой в населенной местности. Вычислить данные монтажной таблицы для температур воздуха от –20 °С до +35 °С через каждые 5 °С. Длина пролета l = 80 м. Климатический район по гололеду II, по ветровому напору – II. Температурные условия:
t°max = +35 °C; t°min = –30 °C; t°э = 0 °С.
Определяем удельные механические нагрузки на провод в пролете.
От собственного веса провода
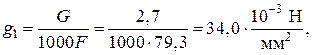 (51)
(51)
где G – вес провода (G = mg – масса провода m = ma + mc = 188 + 88,6 = 276 кг/км (приложение 10.3).
Ускорение силы тяжести g = 9,81 м/с2;
G = 276 ∙ 9,81 ∙ 10–3 = 2,7 Н/м;
F – сечение провода ( F = FA + FC = 68 + 11,3 = 79,3 мм2 (приложение 10.3).
От веса льда
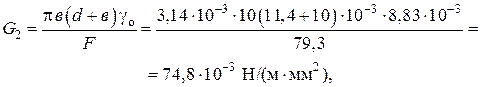 (52)
(52)
где в – толщина слоя гололеда (в = 10 мм = 10×10–3 м (приложение 32); d – диаметр провода (d = 11,4 мм = 11,4×10–3 м (приложение 10.3); γо – удельный вес льда (γо = 0,9×10–3 кг/см3 = 0,9×10–3×9,81 = 8,83×10–3 Н/см3 = 8,83×103 Н/м3).
Суммарная удельная нагрузка от веса провода и веса льда следующая:
g3 = g1 + g2 = (34 + 74,8)×10–3 = 108,8×10–3 Н/(м×мм2).
От давления ветра на провод
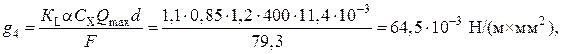 (53)
(53)
где КL – коэффициент, учитывающий длину пролета, КL = 1,1; α – коэффициент, учитывающий неравномерность ветрового напора (α = 0,85, так как Qmax = 400 Па); Сх – коэффициент лобового сопротивления (Сх = 1,2, т.к. диаметр d = 11,4 мм, т.е. d < 20 мм); Qmax – максимальный напор ветра (Qmax = 400 Н/м2 (приложение 33); d – диаметр провода (d = 11,4×10–3 м)..
От давления ветра на провод, покрытый льдом:
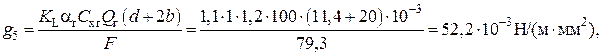 (54)
(54)
где Qг = 0,25 (KL, aL, Cхг, Qг) (приложение 33).
Суммарная удельная нагрузка от веса провода и давления ветра такова:
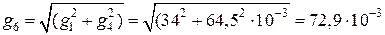 Н/(м×мм2).
Н/(м×мм2).
Суммарную удельную нагрузку от веса провода, льда и давления ветра находят так:
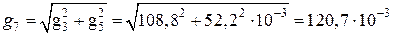 Н/(м мм2).
Н/(м мм2).
Определяем наиболее тяжелые расчетные условия.
Критический пролет
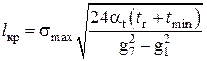 [1], (55)
[1], (55)
где tг – температура гололеда.
Разрывное усилие провода Т = 22980 Н (приложение 10.3).
Предел прочности провода на растяжение
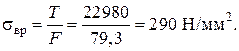
Максимально допустимое напряжение в проводе
Qmax = 0,4σвр = 0,4×290 = 116 Н/мм2.
где коэффициент 0,4 соответствует 40 % (приложение 34).
Температурный коэффициент удлинения αt = 19,2×10–6 (приложение 35).
Подставляем цифровые значения величин в формулу критического пролета, получаем
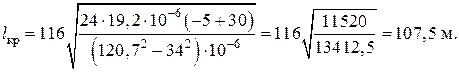
Так как заданный пролет l = 80 м, он меньше критического, поэтому lкр = 107,5 м, то максимальное напряжение в проводе будет при минимальной температуре tmin и нагрузке g1, т.е. σmax при tmin и g1.
Следует проверить напряжение в проводе при среднеэксплуатационной температуре tоэ (сравнив его с σэ доп).
Составляем уравнение состояния провода в пролете. В левой части уравнения подставляем параметры среднеэксплуатационного режима σэ, g1, tэ в правой – параметры максимального режима, т.е. режима, при котором напряжение в проводе максимально. Как уже определено, это режим минимальной температуры, т.е.
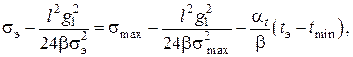 [2] (56)
[2] (56)
где 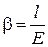 – (модуль упругости Е определен по приложению 35; Е = 80,93 кН/мм2);
– (модуль упругости Е определен по приложению 35; Е = 80,93 кН/мм2);
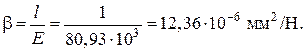
Подставляя цифровые значение величин в уравнение состояния провода в пролете, имеем
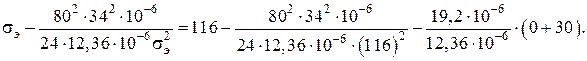
Решаем уравнение относительно σэ:
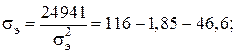
σэ3 – 67,6σэ2 = 24941;
σэ2(σэ – 67,6) = 24941; σэ = 72,3 Н/мм2.
Допустимое значение σэ = 0,3σвр = 0,3×290 = 87 Н/мм2; σэ < σэ доп. Следовательно, самым тяжелым режимом является не среднеэксплуатационный, а режим минимальной температуры tmin и g1.
Определяем максимальную стрелу провеса провода в пролете. Для этого определяем критическую температуру и сравниваем ее с максимальной. При этом, если tmax > tкр, то максимальная стрела провеса будет при максимальной температуре (g1 и tomax). Если же toкр > tomax, то максимальная стрела провеса fmax будет при гололеде (g3, tг):
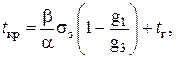 (57)
(57)
где σ3 – напряжение в проводе при гололеде без ветра.
Для определения σ3 составляем уравнение состояния провода в пролете в режиме гололеда без ветра. В первую часть уравнения подставляем параметры максимального режима (tmin, g1, σmax), в левую – параметры режима гололеда без ветра:
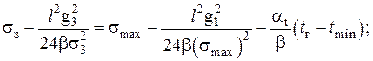 (58)
(58)
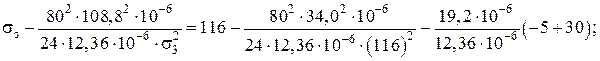
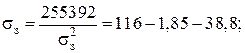
σз2(σз – 75,35) = 255392; σз = 100,6 Н/мм2.
Находим критическую температуру
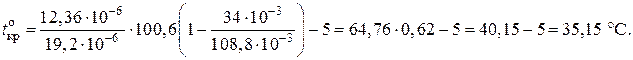
Максимальная температура tоmax = 35 °С, что меньше критической tкр = 35,15 °С. Следовательно, максимальная стрела провеса будет при гололеде (tг, gз, σз)
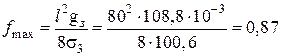 м. (59)
м. (59)
Составляем монтажную таблицу для температур от –20 °С до +35 °С. Для этого нужно определить напряжение в проводе при заданных температурах воздуха при отсутствии ветра и гололеда.
Напряжение в проводе при температуре –20 °С
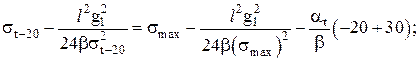 (60)
(60)
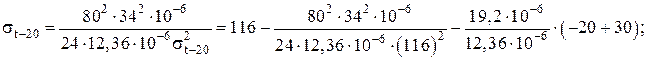
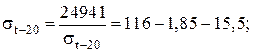
σt–20(σt–20 – 98,65) = 24941; σt–20 = 101,3 Н/мм2.
Тяжение в проводе Н таково:
Т = σF = 101,3 ∙ 79,3 = 8033 Н.
Стрела провеса при tо = –20 °С;
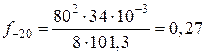 м.
м.
Для других температур напряжение, тяжение и стрелу провеса определяют аналогично, затем данные сводят в табл. 3.1.
Таблица 3.1
Монтажная таблица значений σ, Т, f в зависимости от температуры воздуха
| tо С | σ, Н/мм2 | Т, Н | f, м |
| –20 | 101,3 | 0,27 | |
| –15 | 98,85 | 0,29 | |
| –10 | 86,5 | 0,31 | |
| –5 | 79,5 | 0,34 | |
| 72,3 | 0,37 | ||
| +5 | 65,7 | 0,41 | |
| +10 | 59,5 | 0,46 | |
| +15 | 53,3 | 0,51 | |
| +20 | 47,6 | 0,57 | |
| +25 | 42,7 | 0,64 | |
| +30 | 38,5 | 0,71 |
Дата добавления: 2020-10-14; просмотров: 651;











