Расчет координат пикетов через центральные углы

Центральные углы определяют по формулам (рис. 3):

g₁= 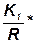r; g_{п= 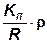;} g_нп=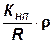

g₁ - центральный угол при точке О между радиусами, проведенными через точку НКК и первый пикет, лежащий на кривой;

g₂ - центральный угол между радиусами ,проведенными через последний пикет на кривой и т. ККК;

g_п - центральный угол ,соответствующий нормальному расстоянию между пикетами;

g_нп - центральный угол ,соответствующий неправильному пикету;

К_1,К₂,K_П,K_НП - длины дуг, соответствующих центральным углам g_1,g_2,g_П,g_НП.

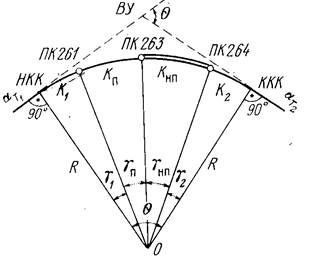
Рисунок 3 – Схема расчета координат пикетов на кривых

Длины дуг К вычисляют по пикетажу.

Контроль вычисления дуг:

К₁+n*К_П+К_НП+К₂ = К,

К - длина круговой кривой.

Контроль вычисления центральных углов:

g₁+n*g_П+g_НП+g_{2 =} q,

n - количество нормальных пикетов;

q - угол поворота трассы.

Координаты центра кривой от точки НКК вычисляют по формулам:

X_O =X_НКК +R* cos.(a_T1+90^o);

Y_O =X_НКК +R* sin(a_Т1+90^О)_,

a_Т1 - дирекционный угол первого тангенса.

Координаты X_O,Y_O контролируют от точки ККК.

Координаты точек на кривой находят по приращениям координат относительно центра кривой. Для этого вычисляют дирекционные углы направлений с центра кривой на соответствующие пикеты, используя дирекционный угол О-НКК:

a_О-НКК=a_Т1+270^О

a_i=a_O-НКК+ 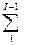g_I

Приращения координат находят по формулам:

DX_i =R* cos.a_i

Dy_i =R* sina_i

Dx _i= R *cos.(a_T1+270^O +g_i)

Dy_i =R* sin(a_T1+270^O+g_i)