Методы построения сетей второго порядка

Полигонометрия

Полигонометрию 2-го порядка строят в виде вытянутых ходов (в случае сетки из одинаковых прямоугольников или квадратов - с равными сторонами), опирающихся на пункты полигонометрии 1-го порядка и прокладываемых по кратчайшему расстоянию между ними. Недостатком полигонометрии является отсутствие взаимной связи между соседними ходами. Поэтому, учитывая важность обеспечения достаточной точности взаимного положения соседних пунктов, следует несколько завышать точность измерений по сравнению с получаемой из расчетов на допуски разбивочных работ и исполнительных съемок. Это относится и к любым другим методам, при применении которых пункты внутри каркаса получают из отдельных взаимно не связанных построений.

Исходя из полученной средней квадратической ошибки ±4.1 см положения пункта, находящегося в середине хода 2-го порядка, получим средний линейный сдвиг в конце хода ±9 см, и предельно допустимую абсолютную невязку хода ± 18 см. При длине хода 1 - 1,5 км это приведет к предельной относительной невязке хода 1: 6 000 - 1: 10 00. Учитывая сказанное выше, не следует прокладывать ходы 2-го порядка с предельной относительной ошибкой более 1: 10 000.

Поскольку сети 2-го порядка служат для определения координат основной массы пунктов строительной сетки, при построении которой одинаково нежелательны деформации как в продольном, так и в поперечном направлении, расчет необходимой точности измерений в полигонометрии выполняют, исходя из принципа равных влияний продольных и поперечных ошибок, т. е. полагая, что ошибка положения пункта равна:

M² = m_t² +m_u² ,

где m_t , m_u - соответственно продольная и поперечная ошибки.

Следует принять:

m_t = m_u =M× .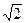

Сдвиг конечной точки вытянутого хода вычисляют по формулам:

; .

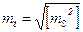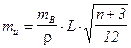Средняя квадратическая ошибка в определении положения пункта в середине вытянутого хода полигонометрии между пунктами каркасной полигонометрии, равна:

m_c = M/2≤ 4.1 мм,

где M- ошибка положения пункта в конце хода , она вычисляется для хода АВ по формулам:

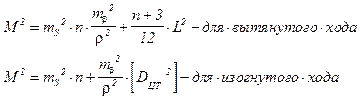
где n -число сторон хода;

[D_ЦТ²] - сумма квадратов расстояний от центра тяжести до текущих точек.

Средняя квадратическая ошибка взаимного положения пунктов CD (рис.48):

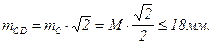
B

C D

A

Рисунок 48.