Метод линейных геодезических засечек

Метод линейных геодезических засечек позволяет сократить число установок светодальномера по сравнению с микротрилатерацией примерно в три раза. Перемещая светодальномер по ходовой линии В₀ - В₁ - В₂ -...- В_r+1, измеряют ее стороны и одновременно расстояния до двух рядов боковых пунктов А₁ - А₂ - А₃ -...- А_к и С₁ - С₂ - ...- С_r (рис. 54), на которых устанавливают только отражатели. В результате получают координаты трех взаимно связанных рядов пунктов строительной сетки.

Рисунок 54 - Метод линейных геодезических засечек[1]

Таблица 11

При этом для линейных сетей используют выражения:

· при оценке точности сторон и координат

; ;

; ;

; ;

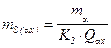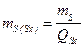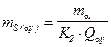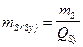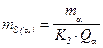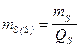K₂ = r² /S (мм),

Q - наибольшие ошибки положения боковых пунктов;

Q_Sx и Q_ax - наибольшие ошибки сторон и дирекционных углов между соседними боковыми пунктами;

Q_Sy и Q_ay - наибольшие ошибки сторон и дирекционных углов между пунктами ходовой линии и соседним боковым;

Q_S и Q_a - наибольшие ошибки сторон и дирекционных углов между боковыми пунктами соседних цепочек.

Рассмотрим пример расчета точности измерений. В сетке квадратов со стороной S =200 м при протяженности цепочки 1 км число пучков засечек r=4. Требуется, чтобы средняя квадратическая ошибка стороны не превышала 10 мм, а ее дирекционного угла 10". Используя вышеуказанные формулы и табл.5, можно решить данную задачу (см. предыдущий способ).

Для того чтобы обеспечить все допуски, примем за окончательный самый жесткий допуск m_{S min} = ±5,0 мм. При этом средняя квадратическая ошибка положения бокового пункта составит М=5,0× 1,96=±9,8 мм.

1.2. ИНЖЕНЕРНО- ГЕОДЕЗИЧЕСКОЕ ПРОЕКТИРОВАНИЕ