Лабораторная работа № 1.

Основные характеристики графа

Цель работы:

1) Изучить понятия вершины, ребра и дуги графа, цикл графа.

2) Рассмотреть понятие дерево.

Литература:

1) "Графы и их применение", Березина Л.Ю., М: Просвещение, 1979г.

2) "Теория графов. Алгоритмический подход", Кристофидес Н.

3) "Применение теории графов в программировании", Евстигнеев В.А. - М.: Наука, 1985г.

Порядок выполнения работы:

I Разработать схему алгоритмов основной программы и подпрограмм.

II Написать и отладить программу на языке Turbo Pascal.

Задание:

Задача Прима-Краскала.

Дана плоская страна и в ней n-городов. Нужно соединить все города телефонной связью так, чтобы общая длина телефонных линий была минимальной.

Другими словами, дан граф с n-вершинами; длины рёбер заданы
матрицей { 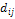}, i,j=1,2,3, ,n. Найти дерево минимальной длины.

Краткие теоретические сведения:

Граф представляет собой непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек.

Ребро, ведущее из вершины в неё же, называется петлей.

Граф без кратных ребер и петель называется простым.

Цепью между вершинами u и v называется последовательность ребер, соединяющих u и v.

Связный граф - это граф, где существует цепь между любой парой вершин u и v; иногда такой граф называют односвязанным.

Циклом называется цепь из V в V.

Деревом называется граф без циклов.

Дерево с n -вершинами имеет n-1 ребер. Поэтому краткое описание поставленной задачи выглядит следующим образом: в цикле n-1 раз делай: Выбрать самое короткое ещё не выбранное ребро при условии, что оно не образует цикла с уже выбранными. Выбранные таким образом ребра образуют искомое дерево.

Кроме того, при проверки того, что новое ребро не образовывает цикла со старыми, используйте следующее: до построения дерена окрасим каждую вершину i в отличный от других цвет i. При выборе очередного ребра, скажем (i, j), где i и j имеют разные цвета, вершина j и все окрашенные в её цвет (т.е. ранее соединенные с ней) перекрашиваются в цвет i. Таким образом, выбор вершин разного цвета обеспечивает отсутствие циклов. После выбора n-1 ребер все вершины получают один цвет.

В заключении анализа алгоритма надо оценить требуемую память и требуемое число операций. С памятью здесь все ясно: в решении удобно хранить n-1 ребер ответа. Всего требуется память 0(n²), т.е. порядка ≈ 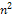, что учитывая реальные величины n, необременительно. Для нахождения текущего минимального ребра надо просмотреть 0( 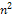) чисел и сделать это n-1 раз, так что временная сложность алгоритма 0( 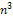). Это тоже реально.

Содержание отчета;

1) Составление алгоритмов.

2) Написание программы на языке Turbo Pascal.

3) Отладка программы.

Контрольные вопросы:

1) Что такое граф?

2) Какой граф называется простым?

3) Что называется цепью?

4) Что такое цикл?

5) Понятие дерева.