Лабораторная работа № 2.
Задание графа матрицей смежности
Цель работы:
1) Изучить понятия полный граф, дополнение графа.
2) Рассмотреть способ задания графа с помощью матрицы смежности.
Литература:
1) "'Графы и их применение". Березина Л.Ю.. М: Просвещение. 1979г.
2) "Теория графов. Алгоритмический подход", Кристофидес Н.
3) "Применение теории графов в программировании". Евстигнеев В.А. - М.: Наука. 1985г.
Порядок выполнения работы:
I
Разработать схему алгоритмов основной программы и подпрограмм.
II
Написать и отладить программу на языке Turbo Pascal.
Задача
Граф задан матрицей смежности
М= 
Изобразить граф, исходя из внешнего вида данной матрицы.
Краткие теоретические сведения:
Матричный эквивалент графа широко используется в работе с графами на ЭВМ.
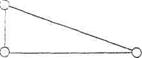
Граф называется полным, если каждые две его вершины соединены одним и только одним ребром.
|
-полный граф
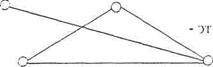
|
| от граф не является полным |
Граф, не являющийся полным, можно преобразовать в полный граф с теми же вершинами, добавив недостающие ребра.
Вершины графа Г и ребра, которые добавлены, также образуют граф, такой граф называется дополнением и обозначается 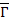 .
.
Каждой вершине графа 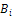 можно поставить в соответствие строку и столбец с номером i, причем
можно поставить в соответствие строку и столбец с номером i, причем
{ 1, если 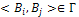
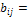
{ 0, если 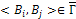
Тогда матрица 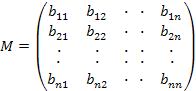 называется матрицей смежностей графа Г и обозначается М(Г).
называется матрицей смежностей графа Г и обозначается М(Г).
Содержание отчета:
1) Составление алгоритмов.
2) Написание программы на языке Turbo Pascal
3) Отладка программы.
Контрольные вопросы:
1) Что такое полный граф?
2) Дайте понятие дополнение графа?
3) Что такое матрица смежностей графа?
4) Как составить матрицу смежностей?
Дата добавления: 2016-07-22; просмотров: 1696;











