Тема 3.3 Минимальная ДНФ.

Уже известно, что произвольная булева функция может быть представлена формулой в дизъюнктивной и конъюнктивной нормальной форме. Равносильными преобразованиями можно получить формулу, содержащую меньшее, чем исходная, число переменных.

Минимальной ДНФ (МДНФ) функции f(x₁, x₂, …, x_n) называется ДНФ, реализующая функцию f и содержащая минимальное число символов переменных по сравнению со всеми другими ДНФ, реализующими функцию f.

Минимальную ДНФ данной формулы можно найти, перебрав конечное число равносильных ей ДНФ и выбрав среди них ту, которая содержит минимальное число переменных. Однако при большом числе переменных такой перебор практически невыполним. Существуют эффективные способы нахождения минимальной ДНФ. Рассмотрим два из них.

Каждый из рассмотренных ниже методов состоит из двух этапов:

· построение сокращенной ДНФ;

· построение матрицы покрытий. Построение МДНФ.

Если для всякого набора а = (а₁, а₂, …, a_n) значений переменных условие g(a)=1 влечет f(a)=1, то функция g называется частью функции f (или функция f накрывает функцию g). Если при этом для некоторого набора с = (с₁, с₂, …, с_n)функция g(c)=1, то говорят, что функция g накрывает единицу функции f на наборе с (или что g накрывает конституенту единицы 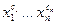функции f).

Конституента единицы функции f есть часть функции f, накрывающая единственную единицу функции f.

Элементарная конъюнкция К называется импликантом функции f, если для всякого набора а = (а₁, а₂, …, a_n) из 0 и 1 условие К(а)=1 влечет f(a)=1.

Определение. Импликант К функции f называется простым, если выражение, получающееся из него выбрасыванием любых множителей, уже не импликант функции f.

Всякий импликант функции f есть часть функции f.

Теорема. Всякая функция реализуется дизъюнкцией всех своих простых импликант.

Сокращенная ДНФ функции f есть дизъюнкция всех простых импликант функции f.

Всякая функция f реализуется своей сокращенной ДНФ. Для всякой функции, не равной тождественно нулю, существует единственная сокращенная ДНФ.

Минимизация формул алгебры логики на кубе. Рассмотрим проблему минимизации для геометрического способа задания формул алгебры логики на кубе.

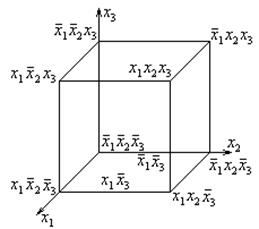Сопоставим различным геометрическим элементам куба (вершинам, ребрам, граням и кубу) конъюнкции различных рангов. Сумма размерности геометрического эквивалента и ранга конъюнкции, ему соответствующей равна числу аргументов формулы алгебры логики.

Каждый геометрический элемент меньшей размерности покрывается геометрическими элементами большей размерности.

Каждая конъюнкция большего ранга покрывается всеми конъюнкциями меньшего ранга.

Геометрические эквиваленты называют интервалами.

Интервал L-го ранга – подмножество вершин куба, соответствующих конъюнкции ранга L.

Например:

Kонъюнкции x соответствует 4 вершины: 100, 101, 110, 111.

На кубе отмечают вершины, где формула алгебры логики равна 1. Эти вершины образуют подмножество Т₁. Для того, чтобы задать ДНФ на кубе, необходимо задать покрытие всех вершин.

Максимальный интервал J – интервал, для которого не существует никакого другого интервала J’ с рангом меньше, чем у J, и такого, что выполняется следующее соотношение .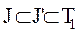

Например:

Пусть есть функция, которая равна 1 в отмеченных точках.
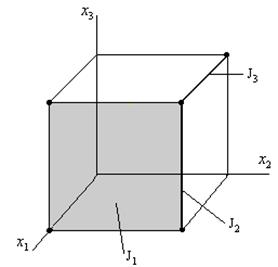J₁ и J₃ – максимальные интервалы,

J₂ – не является максимальным

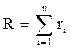
где r_i – ранги конъюнкции, образующих покрытие множества T_1.

Необходимо найти Т₁, при котором R будет минимальным.

Сокращенная ДНФ(СДНФ) – ДНФ, которая соответствует покрытию множества Т₁ всеми максимальными интервалами. В данном примере СДНФ = .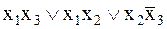

Минимальная ДНФ получается из СДНФ путем выбрасывания из покрытия множества Т₁ максимальными интервалами некоторых “лишних” интервалов.

Тема 3.4 Представление булевой функции в виде минимальной ДНФ.