Общие индексы качественных показателей
Индексы цен показывают, как изменилась стоимость продукции за счет изменения цен.
Агрегатный индекс цен Пааше:
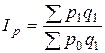 , (7.8)
, (7.8)
где p1q1 – фактическая стоимость продаж (товарооборот) в отчетном периоде;
p0q1 – условная стоимость товаров, реализованных в отчетном периоде по базисным ценам.
Агрегатный индекс цен Ласпейреса:
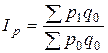 , (7.9)
, (7.9)
где p0q0 – фактическая стоимость продаж (товарооборот) в базисном периоде;
p1q0 – условная стоимость товаров, реализованных в базисном периоде по отчетным ценам.
Индекс цен Пааше показывает изменение цен отчетного периода по сравнению с базисным (на сколько товары стали дороже (дешевле)). Если бы товары были реализованы в отчетном периоде по базисным ценам, то фактическая экономия составила
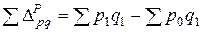 . (7.10)
. (7.10)
Индекс цен Ласпейреса показывает условную экономию, т.е. на сколько изменились цены в отчетном периоде по сравнению с базисным, но по той продукции, которая была реализована в базисном периоде. Этот индекс применяется при прогнозировании объема товарооборота в связи с предлагаемым изменением цен.
В условиях стабильности применяют индекс Пааше, при инфляции – индекс Ласпейреса.
Основываясь на рассмотренных двух вариантах построения индексов, Фишер предложил рассчитывать среднюю геометрическую индексов цен Пааше и Ласпейреса:
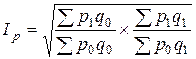 . (7.11)
. (7.11)
Этот индекс носит название “идеальный” индекс цен Фишера. Индекс цен Фишера “обратим” во времени (т.е. если рассчитывать индекс базисного периода к отчетному, он будет равен обратной величине первоначального индекса), но лишен экономического содержания.
При синтезировании общего индекса цен вместо фактического количества товаров (в отчетный и базисный периоды) в качестве соизмерителей индексируемых величин р1 и р0 могут применяться средние величины реализации товаров. При таком способе расчета формула сводного индекса цен (называемого индексом цен Лоу) выглядит следующим образом:
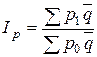 . (7.12)
. (7.12)
Индекс цен Лоу применяется в расчетах при закупках или реализации товаров в течение продолжительных периодов времени (пятилетках, десятилетиях и т.п.), поскольку он дает возможность анализа цен с учетом происходящих внутри отдельных субпериодов изменений в ассортиментном составе товаров.
ПримерПо имеющимся данным о ценах и реализации неоднородных товаров за два периода необходимо определить индексы цен: 1) индивидуальные; 2) агрегатные, в т.ч. а) индекс Пааше; б) индекс Ласпейреса; в) “идеальный” индекс Фишера; г) индекс Лоу.
| Товар | Единица измерения | Базисный период | Отчетный период | ||
| Цена за единицу продукции, руб. | Продано единиц | Цена за единицу продукции, руб. | Продано единиц | ||
| p0 | q0 | p1 | q1 | ||
| А | т | ||||
| Б | м | ||||
| В | шт. |
Сведем расчет индивидуальных индексов цен и промежуточные расчеты для определения агрегатных индексов цен в таблицу:
| Товар | Индивидуальный индекс цен
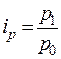
| Стоимость товаров базисного периода, руб. | Стоимость товаров отчетного периода, руб. | Стоимость товаров для среднего за период выпуска, руб. | |||
| в базисных ценах p0q0 | в отчетных ценах p1q0 | в базисных ценах p0q1 | в отчетных ценах p1q1 | базисного периода
p0 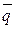
| отчетного периода
p1 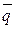
| ||
| А | 1,250 | ||||||
| Б | 1,000 | ||||||
| В | 0,667 | ||||||
| Сумма | — |
а) Индекс цен Пааше
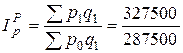 = 1,1391 (113,91%).
= 1,1391 (113,91%).
Абсолютный прирост товарооборота за счет фактора изменения цен в текущем периоде по сравнению с базисным периодом составил
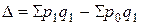 = 327500 – 287500 = 40000 руб.,
= 327500 – 287500 = 40000 руб.,
т.е. если бы уровень цен остался на уровне базисного периода, экономия потребителя составила бы 40000 руб.
б) Индекс цен Ласпейреса
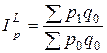
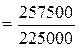 = 1,1444 (114,44%).
= 1,1444 (114,44%).
Абсолютный прирост товарооборота за счет фактора изменения цен в текущем периоде по сравнению с базисным периодом составил
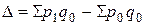 = 257500 – 225000 = 32500 руб.
= 257500 – 225000 = 32500 руб.
в) “Идеальный” индекс цен Фишера
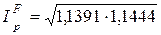 =1,1418 (114,18%).
=1,1418 (114,18%).
г) Индекс цен Лоу
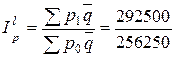 = 1,1415 (114,15%).
= 1,1415 (114,15%).
Товарооборот
Сводный индекс товарооборота:
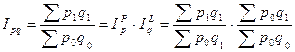 . (7.13)
. (7.13)
Построение моделей взаимосвязанных индексов возможно лишь для сопоставимого круга элементов, т.е. при неизменном ассортименте отдельных товаров в отчетном и базисном периодах.
Абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным одновременно за счет изменения физического объема продаж и изменения цен характеризует разница между числителем и знаменателем индекса, рассчитываемое по формуле (7.3):
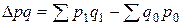 .
.
Измерить изолированное влияние каждого из этих факторов можно через разность числителя и знаменателя соответствующих аналитических индексов.
Разность числителя и знаменателя индекса физического объема (по формуле Ласпейреса)
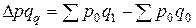 (7.14)
(7.14)
показывает изменение товарооборота за счет роста (сокращения) физического объема продаж.
Разность числителя и знаменателя индекса физического объема (по формуле Пааше)
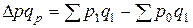 (7.15)
(7.15)
показывает изменение товарооборота в результате роста (снижения) цен.
Абсолютное изменение за счет отдельных факторов в сумме дают общее абсолютное изменение результативного признака:
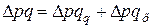 . (7.16)
. (7.16)
Участие каждого фактора в формировании общего изменения товарооборота в относительном изменении определяется по следующим формулам:
· прирост (уменьшение) товарооборота за счет изменения физического объема продаж
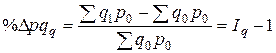 ; (7.17)
; (7.17)
· прирост (уменьшение) товарооборота за счет изменения цен
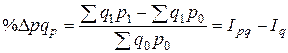 . (7.18)
. (7.18)
Совокупное влияние факторов в относительном выражении отражается моделью
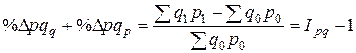 . (7.19)
. (7.19)
При проведении статистического анализа можно определить долю каждого фактора в формировании общего изменения результата:
· доля прироста (уменьшения) товарооборота за счет изменения физического объема продаж
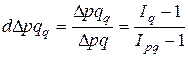 ; (7.20)
; (7.20)
· доля прироста (уменьшения) товарооборота за счет изменения цен
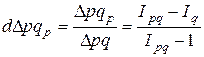 . (7.21)
. (7.21)
При этом 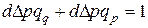 (или 100%). (7.22)
(или 100%). (7.22)
Оценка доли отдельных факторов в формировании результата проводится лишь в случае однонаправленного изменения признаков-факторов.
Дата добавления: 2020-10-01; просмотров: 536;











