Корреляционный анализ
Различают:
- парную корреляцию – это зависимость между результативным и факторным признаком;
- частную корреляцию – это зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков;
- множественную – многофакторное влияние в статической модели
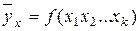 .
.
Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции, который рассчитывается по одной из формул:
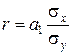 (5.16)
(5.16)
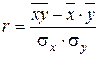 . (5.17)
. (5.17)
Оценка линейного коэффициента корреляции
| Значение r | Характер связи | Интерпретация связи |
| r = 0 | Отсутствует | Изменение x не влияет на изменения y |
| 0 < r < 1 | Прямая | С увеличением x увеличивается y |
| -1 > r > 0 | Обратная | С увеличением x уменьшается y и наоборот |
| r = 1 | Функциональная | Каждому значению факторного признака строго соответствует одно значение результативного |
Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента. Для этого определяется фактическое значение критерия 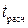 :
:
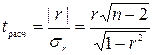 , (5.18)
, (5.18)
Вычисленное по формуле (6.18) значение 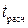 сравнивается с критическим
сравнивается с критическим 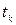 , который получают по таблице Стьюдента с учетом принятого уровня значимости
, который получают по таблице Стьюдента с учетом принятого уровня значимости 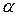 и числа степеней свободы ν. Коэффициент корреляции считается статистически значимым, если tрасч превышает
и числа степеней свободы ν. Коэффициент корреляции считается статистически значимым, если tрасч превышает 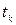 : tрасч >
: tрасч > 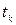 .
.
Универсальным показателем тесноты связи является теоретическое корреляционное отношение:
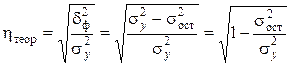 , (5.19)
, (5.19)
где 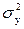 – общая дисперсия эмпирических значений y, характеризует вариацию результативного признака за счет всех факторов, включая х;
– общая дисперсия эмпирических значений y, характеризует вариацию результативного признака за счет всех факторов, включая х;
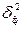 – факторная дисперсия теоретических значений результативного признака, отражает влияние фактора х на вариацию у;
– факторная дисперсия теоретических значений результативного признака, отражает влияние фактора х на вариацию у;
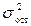 – остаточная дисперсия эмпирических значений результативного признака, отражает влияние на вариацию у всех остальных факторов кроме х.
– остаточная дисперсия эмпирических значений результативного признака, отражает влияние на вариацию у всех остальных факторов кроме х.
По правилу сложения дисперсий:
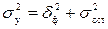 , т.е.
, т.е. 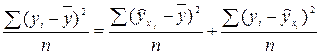 . (5.19)
. (5.19)
Оценка связи на основе теоретического корреляционного отношения (шкала Чеддока)
Значение 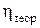
| Характер связи | Значение 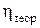
| Характер связи | |
| η = 0 | Отсутствует | 0,5 ≤ η < 0,7 | Заметная | |
| 0 < η < 0,2 | Очень слабая | 0,7 ≤ η < 0,9 | Сильная | |
| 0,2 ≤ η < 0,3 | Слабая | 0,9 ≤ η < 1 | Весьма сильная | |
| 0,3 ≤ η < 0,5 | Умеренная | η = 1 | Функциональная |
Для линейной зависимости теоретическое корреляционное отношение тождественно линейному коэффициенту корреляции, т.е. η = |r|.
Множественный коэффициент корреляции в случае зависимости результативного признака от двух факторов вычисляется по формуле:
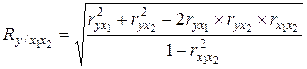 , (5.20)
, (5.20)
где 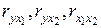 – парные коэффициенты корреляции между признаками.
– парные коэффициенты корреляции между признаками.
Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: 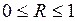 .
.

| Условие включения факторных признаков в регрессионную модель – наличие тесной связи между результативным и факторными признаками и как можно менее существенная связь между факторными признаками. |
Значимость коэффициента множественной детерминации, а соответственно и адекватность всей модели и правильность выбора формы связи можно проверить с помощью критерия Фишера:
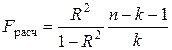 , (5.21)
, (5.21)
где R2 – коэффициент множественной детерминации (R2 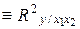 );
);
k – число факторных признаков, включенных в уравнение регрессии.
Связь считается существенной, если Fрасч > Fтабл – табличного значения F-критерия для заданного уровня значимости α и числе степеней свободы ν1 = k,ν2 = n – k – 1.
Частные коэффициенты корреляции характеризуют степень тесноты связи результативного признака и фактора, при элиминировании его взаимосвязи с остальными факторами, включенными в анализ. Расчет частных коэффициентов корреляции в случае двухфакторной регрессии (в первом случае исключено влияние факторного признака х2, во втором – х1):
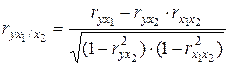 ;
;  , (5.22)
, (5.22)
где r – парные коэффициенты корреляции между указанными в индексе переменными.
Для оценки сравнительной силы влияния факторов, по каждому фактору рассчитывают частные коэффициенты эластичности:
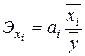 , (5.23)
, (5.23)
где 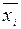 – среднее значение соответствующего факторного признака;
– среднее значение соответствующего факторного признака;
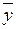 – среднее значение результативного признака;
– среднее значение результативного признака;
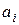 – коэффициент регрессии при i-м факторном признаке.
– коэффициент регрессии при i-м факторном признаке.
Данный коэффициент показывает, на сколько процентов следует ожидать изменения результативного показателя при изменении фактора на 1% и неизменном значении других факторов.
Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется вариацией i-го признака, входящего в множественное уравнение регрессии, рассчитывается по формуле:
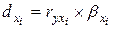 , (5.24)
, (5.24)
где  – парный коэффициент корреляции между результативным и i-м факторным признаком;
– парный коэффициент корреляции между результативным и i-м факторным признаком;
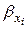 – соответствующий стандартизованный коэффициент уравнения множественной регрессии:
– соответствующий стандартизованный коэффициент уравнения множественной регрессии:
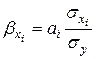 . (5.25)
. (5.25)
Пример
По данным о стоимости основных производственных фондов (СОПФ) и объеме валовой продукции (ВП) определить линейное уравнение связи.
| Номер предприятия | СОПФ ( 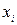 ), млн. руб. ), млн. руб.
| ВП (y), млн. руб. | 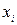 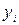
| 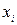 2 2
| 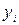 2 2
| 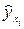
| 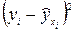
| 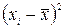
|
| 19,4 | 0,36 | 20,25 | ||||||
| 12,25 | ||||||||
| 30,6 | 0,16 | 6,25 | ||||||
| 36,2 | 27,04 | 2,25 | ||||||
| 41,8 | 3,24 | 0,25 | ||||||
| 47,4 | 73,96 | 0,25 | ||||||
| 2,25 | ||||||||
| 58,6 | 1,96 | 6,25 | ||||||
| 64,2 | 17,64 | 12,25 | ||||||
| 69,8 | 0,04 | 20,25 | ||||||
| Сумма | 125,4 | 82,5 | ||||||
| Среднее | 5,5 | 44,5 | 290,7 | 38,5 | 2248,7 | 44,5 |
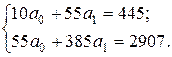
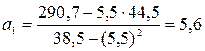 ;
;
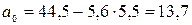 .
.
Уравнение регрессии имеет вид:
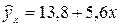 .
.
Следовательно, с увеличением стоимости основных фондов на 1 млн.руб. объем валовой продукции увеличивается в среднем на 5,6 млн. руб.
Проверим значимость полученных коэффициентов регрессии. Рассчитаем 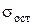 и
и 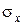 :
:
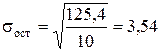
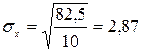
для параметра а0: 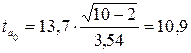
для параметра а1:  .
.
По таблице Стьюдента с учетом уровня значимости 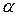 =5% и числа степеней свободы ν =10-1-1=8 получаем
=5% и числа степеней свободы ν =10-1-1=8 получаем 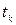 =2,306.
=2,306.
Фактические значения 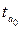 и
и 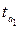 превышают табличное критическое значение
превышают табличное критическое значение 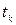 . Это позволяет признать вычисленные коэффициенты корреляции типичными.
. Это позволяет признать вычисленные коэффициенты корреляции типичными.
ПримерПо данным предыдущего примера оценить тесноту связи между признаками, оценить значимость найденного коэффициента корреляции.
 , или
, или 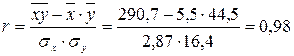 .
.
Значение коэффициента корреляции свидетельствует о сильной прямой связи между рассматриваемыми признаками.
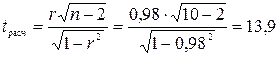
Значение tрасч превышает найденное по таблице значение 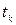 =2.306, что позволяет сделать вывод о значимости рассчитанного коэффициента корреляции.
=2.306, что позволяет сделать вывод о значимости рассчитанного коэффициента корреляции.
ПримерИмеются некоторые данные о среднегодовой стоимости ОПФ (СОПФ), уровне затрат на реализацию продукции (ЗРП) и стоимости реализованной продукции (РП). Считая зависимость между этими показателями линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели.
| СОПФ (х1), млн.руб. | ЗРП (х2), в % к РП | РП (y), млн.руб. | 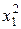
| 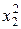
| х1 х2 | х1 y | х2 y | 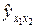
|
| 20,36 | ||||||||
| 20,05 | ||||||||
| 24,21 | ||||||||
| 26,91 | ||||||||
| 30,54 | ||||||||
| 29,08 | ||||||||
| 33,24 | ||||||||
| 35,01 | ||||||||
| 36,25 | ||||||||
| 38,33 | ||||||||
| S = 66 | S = 90 | S = 294 | S = 490 | S = 1018 | S = 688 | S = 2078 | S = 2880 | S = 294 |
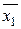 =6,6 =6,6
| 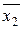 =9,0 =9,0
| 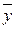 =29,4 =29,4
| – | – | 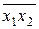 =68,8 =68,8
| 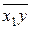 =207,8 =207,8
|  =288,0 =288,0
| – |
Решение. Составим систему нормальных уравнений МНК:
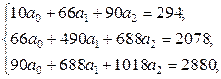
Выразим из 1-го уравнения системы a0 = 29,4 – 6,6·a1 – 9·a2.
Подставив во 2-е уравнение это выражение, получим:
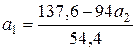 .
.
Далее подставляем в 3-е уравнение вместо a0 и a1 полученные выражения и решаем его относительно a2 с точностью не менее 3-х знаков после запятой. Итак:
a0 = 12,508; a1 = 2,672; a2 = – 0,082; 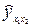 = 12,508 + 2,672·х1 – 0,082·х2.
= 12,508 + 2,672·х1 – 0,082·х2.
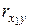 =
= 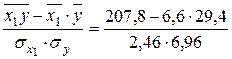 = 0,884;
= 0,884;
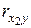 =
=  = 0,777;
= 0,777;
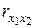 =
= 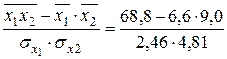 = 0,893;
= 0,893;
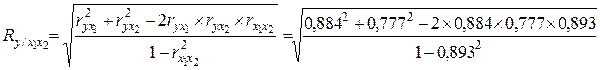 =0,893.
=0,893.
Проверим значимость r (α = 0,01 и ν = 7):
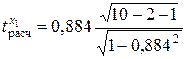 = 5,00;
= 5,00; 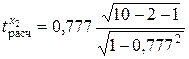 = 3,27.
= 3,27.
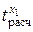 =5,00 > tтабл=3,50 – коэффициент корреляции x1 значим;
=5,00 > tтабл=3,50 – коэффициент корреляции x1 значим;
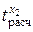 =3,27 < tтабл=3,50 – коэффициент корреляции x2 не значим.
=3,27 < tтабл=3,50 – коэффициент корреляции x2 не значим.
Произведенные расчеты подтверждают условие включения факторных признаков в регрессионную модель – между результативным и факторными признаками существует тесная связь ( 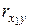 = 0,884;
= 0,884; 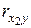 = 0,777), однако между факторными признаками достаточно существенная связь (
= 0,777), однако между факторными признаками достаточно существенная связь ( 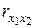 = 0,893). Включение в модель фактора x2 незначительно увеличивает коэффициент корреляции (
= 0,893). Включение в модель фактора x2 незначительно увеличивает коэффициент корреляции ( 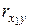 = 0,884;
= 0,884; 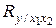 =0,893), поэтому включение в модель фактора x2 нецелесообразно.
=0,893), поэтому включение в модель фактора x2 нецелесообразно.
Вычислим стандартизованные коэффициенты уравнения множественной регрессии:
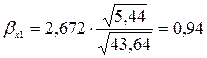
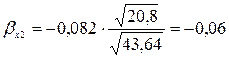
Отсюда вычислим частные коэффициенты детерминации:
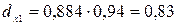
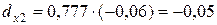
т.е. вариация результативного признака объясняется главным образом вариацией фактора x1.
Вычислим частные коэффициенты эластичности:

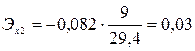
Проверим адекватность модели на основе критерия Фишера:

Найдем значение табличного значения F-критерия для уровня значимости α=0,05 и числе степеней свободы ν1 = 2, ν2 = 10 –2 – 1 : Fтабл=4,74. Превышение значения Fрасч над значением Fтабл позволяет считать коэффициент множественной детерминации значимым, а соответственно и модель – адекватной, а выбор формы связи - правильным.
Ряды динамики
Дата добавления: 2020-10-01; просмотров: 558;











