Принцип работы гидравлического пресса: закон Паскаля и механика жидкости

Принцип действия гидравлического пресса.Гидравлический пресс — это машина, позволяющая приложением малой силы поднимать или создавать давление на огромные грузы, весом в десятки и сотни тонн. Данный эффект, кажущийся на первый взгляд сверхъестественным, имеет строгое научное объяснение, основанное на фундаментальных законах физики жидкостей. В основе работы пресса лежит способность жидкостей передавать оказываемое на них давление. Это свойство кардинально отличает жидкие среды от твердых тел, которые передают усилие преимущественно в направлении его приложения.

Закон Паскаля и передача давления в жидкостях. Ключевым принципом является закон Паскаля, который гласит: давление, производимое на жидкость или газ, передается в любую точку без изменения во всех направлениях. В отличие от жидкости, твердое тело, например, кусок железа, передает приложенную сверху силу преимущественно вниз, не оказывая воздействия на соседние объекты. Эластичные материалы, такие как каучук или гуттаперча, занимают промежуточное положение, частично изменяя направление давления за счет деформации. Однако именно жидкости передают давление абсолютно равномерно по всему объему.

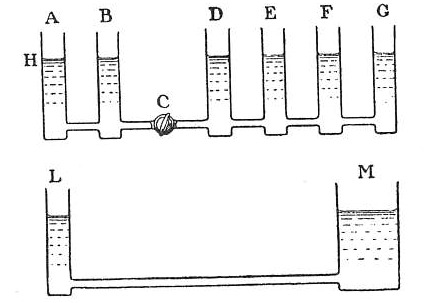
Рис. 26. Схема для уяснения принципа гидравлического пресса

Практические примеры передачи давления жидкостью. Явление передачи давления во всех направлениях объясняет множество наблюдаемых эффектов. Например, огромное давление воды на шлюзовые ворота или плотину возникает потому, что вес вышележащих слоев воды передается не только ко дну, но и к боковым стенкам. При этом давление увеличивается с глубиной. Аналогично, способность судна плавать обусловлена тем, что вода давит на его корпус не только вниз, но и вверх, создавая выталкивающую силу Архимеда.

Экспериментальное объяснение принципа гидравлического пресса. Для понимания работы пресса рассмотрим модель, изображенную на рис. 26. Два цилиндра, А и В, с одинаковым сечением (10 кв.см) соединены у основания трубкой. При наливании воды в цилиндр А уровни в обоих сосудах выравниваются в одной горизонтальной плоскости. Это происходит потому, что давление, создаваемое столбом жидкости и атмосферой, передается по всем направлениям, устанавливая равновесие. Если создать избыточное давление в одном цилиндре (например, переместить поршень), оно мгновенно передастся в другой.

Масштабирование силы в соединенных сосудах. Расширим модель, добавив несколько цилиндров (D, E, F, G), соединенных с основным (А). Если все они имеют одинаковое сечение, то груз, давящий на поршень в А, будет уравновешиваться одинаковыми грузами на поршнях в остальных цилиндрах. Ключевой момент наступает, когда несколько узких цилиндров объединяются в один широкий. Если сечение большого цилиндра М в 50 раз больше сечения малого L, то сила на его поршне будет во столько же раз больше. Таким образом, гидравлический пресс дает выигрыш в силе, пропорциональный отношению площадей поршней.

Конструкция и работа реального гидравлического пресса. В реальном прессе цилиндр L заменяется малым нагнетательным насосом. Усилие оператора, приложенное к рукоятке насоса, дополнительно увеличивается с помощью рычага. Например, усилие в 30 кг, приложенное к рычагу с передаточным отношением 6:1, создает на поршне насоса давление, эквивалентное 180 кг. Если площадь поршня пресса (М) больше площади поршня насоса (L) в 100 раз, то создаваемое усилие достигнет 18 000 кг (18 тонн).

Компенсация выигрыша в силе: «золотое правило» механики. Кажущийся выигрыш в силе подчиняется «золотому правилу» механики: во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии. Чтобы поднять 18-тонный груз на 1 см, поршень малого насоса должен пройти путь в 100 раз больший (при соотношении площадей 1:100), а с учетом рычага — путь оператора может быть в 600 раз длиннее. Кроме того, часть работы неизбежно теряется на преодоление силы трения. Таким образом, природа не создает энергии из ничего, а лишь преобразует работу, взимая «комиссию» на трение.

Заключение. Гидравлический пресс — блестящая иллюстрация практического применения закона Паскаля. Его работа демонстрирует фундаментальный принцип механики: сохранение энергии при преобразовании силы и расстояния. Это устройство не создает энергию, а позволяет малой силе, приложенной на большом пути, совершить работу по подъему огромного груза на малое расстояние, оставаясь одним из самых эффективных инструментов в современной промышленности.

Закон Паскáля и парадокс давления жидкости в сосудах разной формы

Гидравлический пресс позволяет многократно увеличивать прилагаемое усилие за счет передачи давления через жидкость. Для этого необходимы поршни, создающие давление на воду, которое, в свою очередь, воздействует на поднимаемый груз. Аналогичный выигрыш в силе достигается с помощью рычага. Оба принципа широко применяются в различных механизмах и машинах.

Простейший пример рычага — качели из доски, перекинутой через бревно. Если вес детей различен, равновесие достигается, когда более легкий ребенок садится на более длинное плечо. Рычаг находится в равновесии, когда длины его плеч обратно пропорциональны приложенным силам. Это фундаментальное правило механики.

Однако в ряде устройств требуется увеличить давление жидкости без использования поршней или рычагов. Возникает вопрос: как это возможно? Рассмотрим два цилиндрических сосуда (рис. 27) с одинаковой площадью дна в 1 кв. дм, но разной высотой: один и два дециметра. Их объем составляет 1 и 2 литра соответственно.

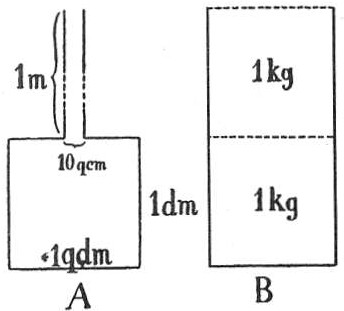
Рис. 27: Два цилиндрических сосуда разной высоты с одинаковой площадью дна. К первому присоединена вертикальная трубка малого сечения.

Если к первому сосуду герметично присоединить узкую трубку сечением 0,1 кв. дм и длиной 1 метр, то в ней поместится еще 1 кг воды. Полное давление на дно такого составного сосуда окажется равным 11 кг, хотя общий вес воды — лишь 2 кг. Этот кажущийся парадокс требует экспериментального доказательства и объяснения.

Для точного измерения давления жидкости на дно используется специальный прибор. Сосуд имеет подвижное, идеально отшлифованное дно, которое играет роль чаши весов (рис. 28). Гири на противоположной чаше уравновешивают давление воды, не давая дну оторваться.

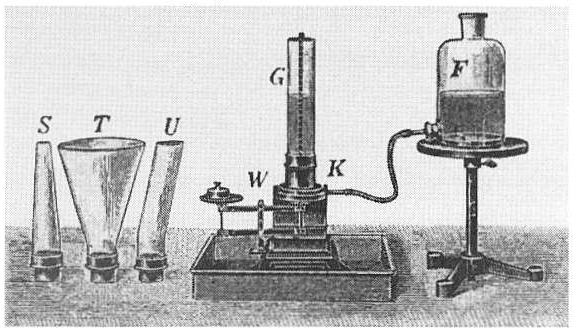
Рис. 28: Прибор для измерения давления жидкости на дно. Подвижное дно А уравновешивается гирями. Изображены сосуды разной формы: G (цилиндрический), Т (расширенный), S (суженный), U (изогнутый).

Если с помощью этого прибора исследовать сосуды разной формы, но с одинаковой площадью дна, обнаруживается ключевой закон. Давление на дно определяется не весом жидкости в сосуде, а исключительно высотой ее столба над дном и площадью самого дна. Форма сосуда не имеет значения.

Таким образом, в цилиндрическом сосуде давление равно весу жидкости. В расширенном кверху сосуде давление на дно меньше общего веса, так как часть силы поддерживается наклонными стенками. В суженном сосуде давление, напротив, может превышать общий вес жидкости, что кажется противоречивым.

Парадокс с сосудом и узкой трубкой (рис. 27) является частным случаем этого закона. Составной сосуд можно рассматривать как суженный кверху. Давление создается весом узкого, но высокого столба жидкости. Закон был открыт Блэзом Паскалем, доказавшим, что давление в жидкости передается одинаково по всем направлениям.

Для понимания явления рассмотрим сосуд ступенчатой формы, расширяющийся кверху (рис. 29). Площади ступеней АВ, CD и EF относятся как 1:9:25 кв. дм при высоте каждой 1 дм. Общий вес воды — 35 кг, однако давление на дно АВ составляет лишь 3 кг.

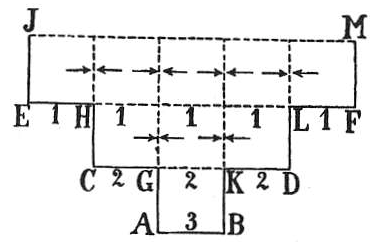
Рис. 29: Ступенчатый сосуд, расширяющийся кверху. Площади ступеней относятся как 1:9:25.

Объяснение заключается в том, что давление в жидкости передается во все стороны. Боковые давления от водяных масс на разных ступенях взаимно уравновешиваются. В итоге на дно давит только вес вертикального водяного столба, находящегося непосредственно над ним.

Аналогичный анализ применим к ступенчатому сосуду, сужающемуся кверху (рис. 30). Здесь, при том же общем весе воды в 35 кг, давление на широкое дно площадью 25 кв. дм составит уже 75 кг. Каждый квадратный дециметр основания испытывает давление, соответствующее высоте всего столба жидкости.

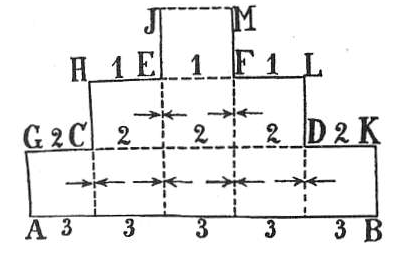
Рис. 30: Ступенчатый сосуд, сужающийся кверху. Давление на дно превышает общий вес жидкости.

Возникает мнимое противоречие: куда девается разница между давлением на дно (75 кг) и весом сосуда на весах (35 кг)? Ответ: стенки сосуда испытывают значительное давление снизу вверх со стороны жидкости. Эта подъемная сила (40 кг) компенсирует избыточное давление, поэтому весы показывают только истинный вес воды.

Эти рассуждения справедливы и для сосудов с плавно изменяющимся сечением. Давление жидкости на горизонтальное дно зависит только от плотности жидкости, высоты ее столба и площади дна. Этот принцип лежит в основе действия гидравлического пресса и других устройств.

Вернемся к исходному примеру. В сосуде с тонкой трубкой (рис. 27, А) давление на дно создается высоким столбом жидкости в трубке. Если длина трубки составит 10 м при сечении 1 кв. см, давление достигнет 101 кг, хотя масса воды останется 2 кг. Именно этот эффект использовал Паскаль в знаменитом опыте, когда бочка лопнула под давлением воды в длинной вертикальной трубке.

Практическое применение этого явления реализовано в экстрактном прессе Реаля. Для ускорения экстракции веществ из растительного сырья через него пропускают растворитель под высоким давлением, создаваемым длинным вертикальным столбом жидкости. Это подтверждает фундаментальность открытых законов гидростатики.

Сведения об авторах и источниках:

Авторы: В. Гампсон, К. Шеффер

Источник: Парадоксы природы

Данные публикации будут полезны студентам физических и технических специальностей, изучающих механику и принципы работы простых механизмов, начинающим инженерам и конструкторам, интересующимся эргономикой и оптимизацией транспортных средств, а также всем, кто увлекается историей техники и неочевидными физическими явлениями в повседневной жизни.