Пример решения транспортной задачи методом потенциалов
Решить методом потенциалов транспортную задачу:
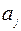
| ||||
| 3 | 8 | 2 | ||
| 7 | 4 | 8 | ||
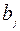
| = |
Опорный план этой задачи найден методом северо-западного угла.
Приписываем к таблице строку для платежей 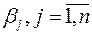 и столбец для платежей
и столбец для платежей 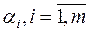 . Псевдостоимости записываем в левом углу клетки, а стоимости – в правом.
. Псевдостоимости записываем в левом углу клетки, а стоимости – в правом.
Из условий 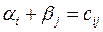 в базисных клетках получаем систему уравнений:
в базисных клетках получаем систему уравнений:
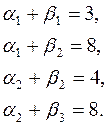
Полагая 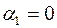 , находим платежи
, находим платежи 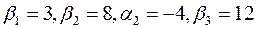 и псевдостоимости для свободных клеток. Получаем таблицу
и псевдостоимости для свободных клеток. Получаем таблицу
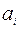
| 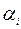
| ||||
| 15 3 | [-] 20 8 | 12[+] 2 | |||
| -1 7 | [+] 0 4 | [-] 30 8 | -4 | ||
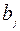
| = | ||||
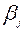
|
Стоимость перевозок по плану этой таблицы:
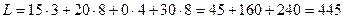 .
.
Так как клетка (1,3) имеет отрицательную цену 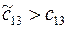 , то план не является оптимальным. Строим для клетки (1,3) цикл. Цена цикла
, то план не является оптимальным. Строим для клетки (1,3) цикл. Цена цикла 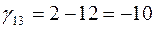 . По циклу переносим 20 единиц груза (больше нельзя, чтобы перевозки в клетке (1,2) не стали отрицательными). При этом стоимость плана изменяется на
. По циклу переносим 20 единиц груза (больше нельзя, чтобы перевозки в клетке (1,2) не стали отрицательными). При этом стоимость плана изменяется на 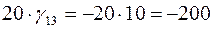 . Для нового плана вычисляем новые значения платежей и псевдостоимостей:
. Для нового плана вычисляем новые значения платежей и псевдостоимостей:
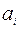
| 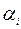
| ||||
| [-]15 3 | -2 8 | [+] 20 2 | |||
| 9 [+] 7 | 20 4 | [-] 10 8 | |||
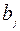
| = | ||||
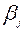
| -2 |
Стоимость перевозок по плану этой таблицы:
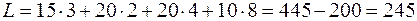
Полученная таблица имеет клетку (2,1) с отрицательной ценой 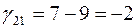 . По циклу этой клетки переносим 10 единиц груза, при этом стоимость плана уменьшается на
. По циклу этой клетки переносим 10 единиц груза, при этом стоимость плана уменьшается на 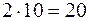 единиц, и получаем новый опорный план с новой системой платежей и псевдостоимостей:
единиц, и получаем новый опорный план с новой системой платежей и псевдостоимостей:
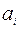
| 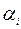
| ||||
| 5 3 | 0 8 | 30 2 | |||
| 10 7 | 20 4 | 5 8 | |||
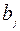
| = | ||||
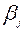
|
Стоимость перевозок по плану этой таблицы:
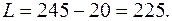
Так как в последней таблице все псевдостоимости не превосходят соответствующих стоимостей, то полученный опорный план 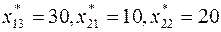 является оптимальным. Стоимость перевозок при этом
является оптимальным. Стоимость перевозок при этом 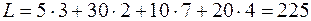 .
.
Дата добавления: 2020-10-01; просмотров: 520;











