Пример решения задачи двойственным симплекс-методом

Решить задачу ЛП двойственным симплекс-методом:

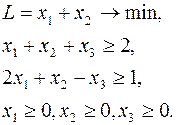
Приводим задачу к каноническому виду:

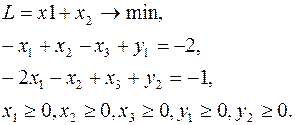
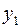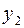Знаки в ограничениях заменили противоположными для того, чтобы переменные и можно было взять в качестве базисных. Симплексная таблица имеет вид

	b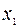
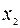
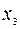
L		-1	-1
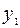
	-2	-1		-1
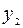
	-1	-2	-1

Таблица двойственно-допустимая, но не оптимальная. Выбираем ведущую строку – это строка переменной 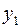, ведущий столбец – это столбец переменной 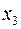. После преобразования таблица принимает вид

	b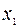
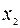
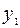
L		-1	-1
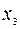
			-1	-1
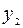
	-3	-3

Так как в столбце b есть отрицательная переменная 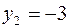, то эту строку выбираем ведущей, а столбец переменной 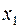будет ведущим столбцом. После преобразования получаем таблицу:

	b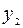
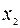
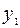
L		-1/3	-1	-1/3
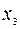
		1/3	-1	-2/3
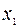
		-1/3		-1/3

которая является оптимальной. Соответствующее оптимальное решение имеет вид .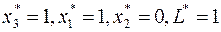

Двойственность в ЛП

Постановка задачи

Рассмотрим пару задач ЛП вида:

(I) (II)

… …

… …

… …

… …

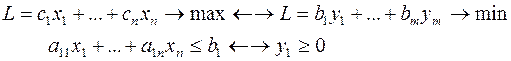
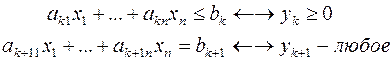
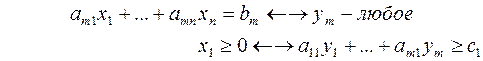
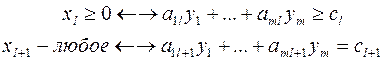
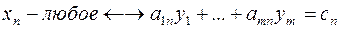
Задачу (I) называют прямой задачей ЛП, а (II) – двойственной. Неравенства задач (I) и (II), соответствующие друг другу (по стрелке), называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т. е. соотношение двойственности взаимное. Поэтому можно из такой пары задач любую считать прямой, а другую – двойственной.