Пример решения задачи ЦЛП

Решить задачу ЦЛП:

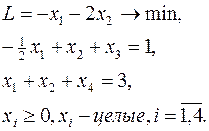
Решаем задачу без условия целочисленности симплекс-методом. Оптимальная таблица имеет вид

	b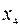
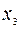
L	-14/3	-4/3	-2/3
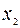
	5/3	1/3	2/3
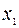
	4/3	2/3	-2/3

Оптимальное решение 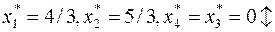не является целочисленным. Выберем среди нецелочисленных переменных 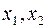переменную 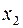с максимальной дробной частью и построим соответствующее отсечение:

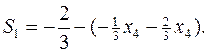
Приписывая это ограничение к симплексной таблице, и проводя стандартное преобразование двойственным симплекс-методом, получим:

	b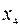
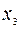
L	-14/3	-4/3	-2/3
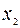
	5/3	1/3	2/3
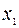
	4/3	2/3	-2/3
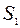
	-2/3	-1/3	-2/3

	b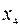
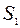
L	-4	-1	-1
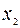
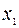
			-1
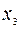
		1/2	-3/2

Полученная таблица является оптимальной. Соответствующее оптимальное решение 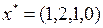является целочисленным. Значение функции на этом решении .

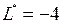Транспортная задача ЛП

Постановка задачи

Классическая транспортная задача ЛП формулируется следующим образом. Имеется m пунктов производства (поставщиков) и n пунктов потребления (потребителей) однородного продукта. Заданы величины:

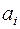- объем производства (запас) i-го поставщика, ;

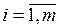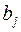- объем потребления (спрос) j-го потребителя,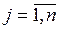

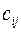- стоимость перевозки (транспортные затраты) единицы продукции от i-го поставщика к j-му потребителю.

Требуется составить такой план перевозок, при котором спрос всех потребителей был бы выполнен, и при этом общая стоимость всех перевозок была бы минимальна [1,3].

Транспортная задача, в которой суммарные запасы 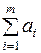и суммарные потребности 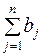совпадают, называется закрытой моделью; в противном случае – открытой. Открытая модель решается приведением к закрытой модели.

Математическая закрытая модель транспортной задачи имеет вид

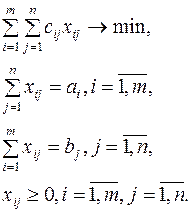
В случае, когда суммарные запасы превышают суммарные потребности, то есть 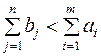, вводится фиктивный n+1 потребитель, потребности которого .

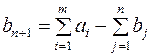В случае, когда суммарные потребности превышают суммарные запасы, то есть 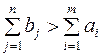, вводится фиктивный m+1 поставщик, запасы которого .

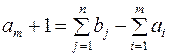Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится.

Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к закрытой модели.

5.2. Построение опорного плана транспортной задачи

Методы решения транспортной задачи сводятся к простым операциям с транспортной таблицей, которая имеет вид:

		…	n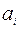
		…
…	…	…	…	…
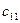
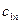
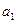
m		…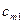
		…		=

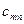
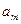
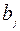
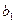
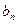
Базисными клетками транспортной таблицы являются клетки с отличными от нуля положительными перевозками, остальные клетки – свободные. Базисные клетки образуют опорный план транспортной задачи, еcли выполняются два условия:

сумма перевозок в каждой строке равна запасу 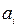в данной строке;

сумма перевозок в каждом столбце равна соответствующему спросу .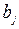

Опорный план транспортной задачи содержит не более 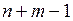отличных от нуля перевозок .

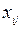Опорный план называется вырожденным, если число ненулевых перевозок 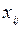меньше 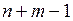, опорный план – невырожденный, если число ненулевых перевозок равно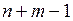

Рассмотрим способы построения опорного плана в невырожденном и вырожденном случаях [1,3].