Вопрос 4. Волновые и корпускулярные свойства микрочастиц, электрона.

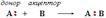Французский ученый Луи де Бройль (1882—1987) осознавая существующую в природе симметрию и развивая представления о двойственной корпускулярно-волновой природе света, выдвинул в 1923 г. гипотезу об универсальности корпускулярно-волнового дуализма. Он утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.

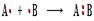Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики — энергия E и импульс p, а с другой стороны — волновые характеристики — частота и длина волны.

Так как дифракционная картина исследовалась для потока электронов, то необходимо было доказать, что волновые свойства присущи каждому электрону в отдельности. Это удалось экспериментально подтвердить в 1948 г. советскому физику В. А. Фабриканту. Он показал, что даже в случае столь слабого электронного пучка, когда каждый электрон проходит через прибор независимо от других, возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электронов в десятки миллионов раз более интенсивных.

Современная трактовка корпускулярно-волнового дуализма может быть выражена словами физика В. А. Фока (1898—1974): «Можно сказать, что для атомного объекта существует потенциальная возможность проявлять себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом. Именно в этой потенциальной возможности различных проявлений свойств, присущих микрообъекту, и состоит дуализм волна — частица. Всякое иное, более буквальное, понимание этого дуализма в виде какой-нибудь модели неправильно»

Свойства волновой функции

Отметим свойства волновой функции ψ в частном случае трёхмерного пространства в декартовых координатах. В этом случае ψ зависит от трёх переменных (X,Y,Z) и имеет следующие свойства :

1. Импульс частицы в каждом из направлений (X,Y,Z) пропорционален первой производной волновой функции, делённой на саму волновую функцию, а именно

где — импулсы,.

2. Кинетическая энергия частицы 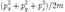пропорциональна второй производной, или кривизне волновой функции, деленной на саму волновую функцию.

3. Абсолютная величина квадрата функции (то есть сумма возведённых отдельно в квадрат мнимой и действительной частей функции ) равна вероятности нахождения частицы в точке с координатами . Это свойство противоречит законам классической механики, в которой положение частиц в данный момент времени фиксировано. Одно из мнимых ограничений квантовой механики состоит в том, что она с достоверностью определяет лишь время (или, точнее говоря, вероятность) нахождения частицы в данном положении . В квазиклассическом пределе волновые функции локализуются в дельта-функции, а центры их сосредоточения движутся по классическим траекториям согласно уравнениям Ньютона.