В координатах дебит–депрессия
Обработка индикаторных линий в этих координатах предполагает, что пластовое давление известно.
Выбор алгоритмов обработки индикаторных линий производится после графического построения индикаторной линии.
Ниже приведены основные алгоритмы обработки типовых индикаторных линий, в зависимости от закона фильтрации жидкости в пласте.
Л и н е й н ы й з а к о н ф и л ь т р а ц и и
В основу обработки положено уравнение прямой линии вида:
DPi=AQi (5.6)
где DPi – депрессия на режиме исследования i, МПа;
А=1/h постоянная уравнения, величина, обратная коэффициенту продуктивности скважины, сут×МПа/м3;
Qi – дебит скважины на режиме, м3/сут.
Коэффициент продуктивности скважины определяется по формуле
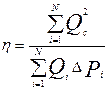 (5.7)
(5.7)
Для проверки точности определения коэффициента продуктивности скважины вычисляется расчетная депрессия на режимах
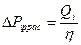 (5.8)
(5.8)
и сумма квадратов отклонений между расчетной и фактической депрессиями
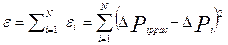 (5.9)
(5.9)
Н е л и н е й н ы й з а к о н ф и л ь т р а ц и и
При обработке криволинейных (вогнутых в сторону оси дебитов) индикаторных линий рекомендуется применять две методики, одна из которых приведена ниже. При этом выбор параметров производится по минимуму суммы квадратов отклонений emin между расчетной и фактической депрессиями.
Ниже приводится порядок обработки результатов исследований.
Методика 1.Двучленный квадратичный закон фильтрации
Формула для определения притока жидкости имеет следующий вид
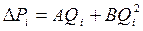 (5.10)
(5.10)
где B – постоянная уравнения, характеризующая инерционные сопротивления в пласте.
Для графического определения параметров А и В уравнение (5.10) перестраивается в координатах DPi/Qi и Qi
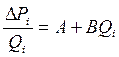 (5.11)
(5.11)
Коэффициент А определяется как отрезок, отсекаемый полученной прямой на оси кординат, коэффициент В – как тангенс угла наклона прямой к оси абсцисс.
Коэффициенты А=1/h и В уравнения (5.11) могут быть определены численным методом по формулам:
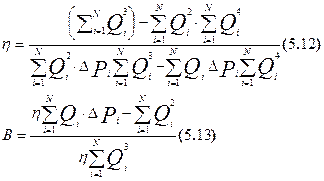
Cуммы берутся по всем измерениям DPi и Qi .
Вычисляются расчетная депрессия DPiрасч на каждом режиме
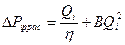 (5.14)
(5.14)
и сумма квадратов отклонений e2 между расчетной депрессией и фактической по формуле (5.9)
Для обработки ИЛ в случаях необходимости также используют составной закон фильтрации.
5.2.ИССЛЕДОВАНИЕ СКВАЖИН ПРИ НЕУСТАНОВИВШИХСЯ РЕЖИМАХ ФИЛЬТРАЦИИ
В общем комплексе гидродинамических исследований скважин методы исследования по наблюдениям нестационарных процессов метод восстановления (падения) давления, гидропрослушивание, экспресс-методы нашли широкое применение. Эти методы в отличие от метода пробных откачек имеют большую разрешающую способность. Они позволяют раздельно оценить параметры призабойной и удаленной зоны пласта, неоднородность и выявить литологические экраны.
Кроме задач, связанных с изучением коллекторских свойств пласта и его строения, методы исследования скважин при нестационарной фильтрации в последнее время широко используются в решении задач контроля процессов разработки. Наиболее важным параметром контроля является определение текущей нефтенасыщенности пласта.
Немалое значение приобретают методы нестационарной фильтрации при зондировании и оценке эффективности воздействия на призабойную зону скважин и на весь продуктивный пласт.
При исследовании скважин часто встречаются кривые восстановления давления, по форме сильно отличающиеся от идеальных - теоретических кривых. Важным является объяснение и оценка факторов, определяющих форму кривых восстановления давления. К ним относят технологические факторы и факторы, связанные с неоднородностью коллектора.
Из технологических факторов наибольшее значение имеет приток жидкости в скважину после ее остановки. В практике широкое применение нашли методы обработки кривых восстановления давления с учетом притока жидкости в скважину. Одним из условий, определяющих достоверность кривых восстановления давления, является достаточно стабильный режим работы скважины перед ее остановкой. Иногда по целому ряду причин эти условия не удается реализовать. В этом случае исследование скважин осуществляется экспресс - методом.
Приведем ниже наиболее распространенную схему исследований скважин на неустановившемся режиме фильтрации.
Скважина до исследования работала продолжительное время Т на квазиустановившемся режиме при Q = const . Затем в какой-то момент, принимаемый в дальнейшем за t=0,скважину закрывают. После остановки скважины замеряются изменяющиеся во времени забойные давления Pc(t) и устьевые Pб(t) и Pк(t) давления. Эта схема, наиболее распространена на практике и получила название метод кривых восстановления давления (КВД).
 Q
Q
Qo
t
|
Мгновенное прекращение притока жидкости в скважину после ее остановки аналитически можно представить как наложение отрицательного дебита, равного по величине предыдущему (рис. 1.20 ) .
При достаточно большом периоде работы Т скважины до остановки, по сравнению с периодом восстановления давления, т. е. при Т>>1, второй член в этой формуле можно принять постоянным.
Тогда, очевидно, должно быть сохранено равенство

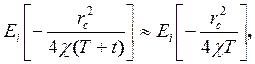 (5.16)
(5.16)
найдем перепад давления в момент времени Т
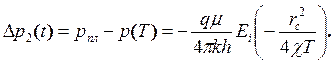 (5.17)
(5.17)
Вычитая третье уравнение из первого, имея в виду второе, и заменяя интегральную показательную функцию ее выражением для малого аргумента, найдем депрессию в момент времени Т, отсчитываемую от забойного давления,
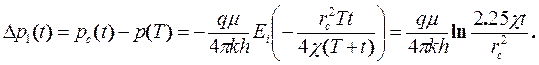 (5.18)
(5.18)
Данное уравнение прямой в координатах Dр1(rc,t), 1n t. Таким образом, перестраивая кривую восстановления давления в координатах Dр1(rc,t), 1n t получим прямую (рис.1.21). По наклону этой прямой к оси абсцисс и отрезку, отсекаемому на оси ординат В, найдем параметры пласта:
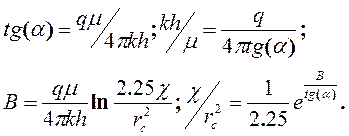

Допущение о постоянстве Ei(…) равноценно предположению, что забойное давление в скважине было бы постоянным, если бы скважина в момент t не была остановлена, а продолжала работать. Такое допущение не всегда можно делать.
Если период работы скважины до ее остановки Т соизмерим с периодом наблюдения t после остановки, обрабатывать такие кривые восстановления давления по (5.18) нельзя. В этом случае, заменяя интегральную, показательную функцию ее выражением для малого аргумента, получим
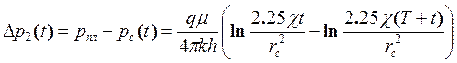 (5.19)
(5.19)
или
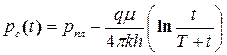 (5.20)
(5.20)
Формула (5.20) позволяет, так же как и (5.18), определять параметр гидропроводности по кривой восстановления давления, преобразованной в координатах Dрc(t), 1n [t/(T+t)]. Этот метод получил название - метод Хорнера. Он не позволяет определить параметр crc ,но дает возможность определить пластовое давление.
При бесконечно длительном наблюдении, когда t>>Т, выражение t/(Т+t)–>1,
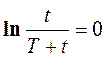 (5.21)
(5.21)
 Тогда, если экстраполировать прямолинейные участки кривой восстановления давления до пересечения с осью ординат (см. рис.1.22), найдем пластовое давление.
Тогда, если экстраполировать прямолинейные участки кривой восстановления давления до пересечения с осью ординат (см. рис.1.22), найдем пластовое давление.
Пример. Пусть скважина, проработавшая до остановки в течение 48 ч, остановлена на восстановление давления. На рис. 1.23 приведена обработка гипотетической кривой восстановления безразмерного давления по методу касательной - формула (5.18) (кривая 2) и методу Хорнера – формула (5.20) (прямая 1). Кривая восстановления давления в координатах рc(t), 1п(t) представлена прямой линией только на начальном участке. Спустя примерно t=2,5 ч (1п t=9) после остановки скважины, что составит t=0,05 Т, кривая восстановления давления начинает отклоняться от прямой.
Кривая восстановления давления, обработанная по методу Хорнера, на всем участке представлена прямой линией. Этот пример указывает на то, что обработку кривых восстановления давления без учета времени работы скважины до ее остановки можно проводить до момента t<0,05 Т. Участки кривых восстановления давления, соответствующие t>0,05 Т, нужно обрабатывать методом Хорнера.
 Рассмотренные два метода обработки кривых восстановления давления разработаны для бесконечного пласта или для таких периодов исследования, когда влияние границ пласта практически не сказывается на кривых восстановления давления.
Рассмотренные два метода обработки кривых восстановления давления разработаны для бесконечного пласта или для таких периодов исследования, когда влияние границ пласта практически не сказывается на кривых восстановления давления.
И. А. Чарным был предложен метод обработки кривых восстановления давления в ограниченных пластах. Исходным уравнением этого метода является
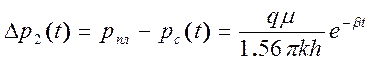 (5.22)
(5.22)
где
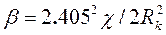 (5.23)
(5.23)
Формула (5.23) следует из решения Маскета, полученного для случая дренирования ограниченного пласта с постоянным давлением на контуре, единичной скважиной с постоянным дебитом q. Решение представляет бесконечный ряд функций Бесселя. Ограничение этого ряда первым членом сводит решение к (5.23). Это указывает на то, что (5.23) справедлива для больших моментов времени.
Логарифмируя (1.23), получим
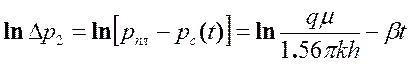 (5.24)
(5.24)
Если перестроить кривую восстановления давления в координатах 1п Dр2, t, получим прямую (рис. 1.24), по наклону которой к оси абсцисс найдем b, а по отрезку, отсекаемому на оси ординат, В=1п qm,/(1,56pkh).
Зная b и В, найдем параметры пласта:
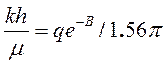 (5.25)
(5.25)
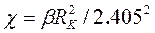 (5.26)
(5.26)
Обработка кривых восстановления давления по (5.24) требует знания пластового давления. При неизвестном пластовом давлении И. А. Чарным был предложен другой способ обработки кривых восстановления давления – дифференциальный. Исходной в этом методе является формула
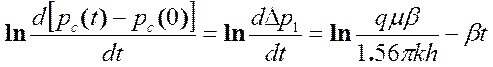 (5.27)
(5.27)
где рc (0) – забойное давление в скважине до ее остановки.
Перестраивая кривую восстановления давления в координатах ln d (Dp1 / dt), t, получим прямую; по углу наклона ~ найдем пьезопроводность по (5.26) (если известен радиуc контура питания), а по отрезку, отсекаемому на оси ординат В1 и b, найдем гидропроводность пласта
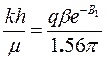 (5.28)
(5.28)
Расчетная схема для конечного пласта пока не получила широкого применения при гидродинамических исследованиях скважин. Ограничение этого метода вызвано тем, что в практике нет малых по размеру пластов с постоянным давлением на контуре. Однако эта схема столь же жизненна, как и схема бесконечного пласта. Прежде всего, в пласте, разрабатываемом множеством скважин, существует для каждой скважины зона дренирования с давлением, которое можно принять как среднее давление на контуре дренирования. В этом смысле правомерность применения схемы ограниченного пласта, пожалуй, такая же, как и допущение существования в пласте установившегося состояния, правомерность применения решения для бесконечного пласта к отдельным скважинам в системе скважин.
Кроме того, этот метод может найти широкое применение при исследовании очаговых скважин, и особенно при разработке залежей высоковязких нефтей.
В этом случае при закачке воды, а тем более пара, соотношение вязкостей может достигать сотен и тысяч единиц, а следовательно подвижность (k/m) в зоне закачки будет также резко отличаться от подвижности за фронтом вытеснения.
В этом случае за контур питания Rk можно принять контур вытеснения, а за давление рk – давление на этом контуре. Тогда применение расчетной схемы ограниченного пласта приобретает первостепенное значение с точки зрения кон-троля за разработкой и вытеснением нефти. Применение схемы ограниченного пласта совместно со схемой бесконечного пласта перспективно при оценке состояния призабойной зоны - позволяет определить параметр Rk/rc.По схеме бесконечного пласта можно, например, определить c/гc , по схеме конечного пласта по (5.26) – c/Rk2. Тогда
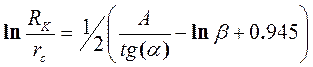 (5.29)
(5.29)
где А и a - соответственно отрезок, отсекаемый на оси ординат, и угол наклона кривой восстановления, обработанной по схеме бесконечного пласта; b - угол наклона кривой восстановления давления, обработанной по схеме конечного пласта.
Рассмотренные методы обработки кривых восстановления давления получены для идеальных условий. Фактические кривые восстановления давления часто бывают осложнены влиянием различных факторов, которые не учтены при изложении методов для их обработки.
Факторы, определяющие форму кривых восстановления
давления
На форму кривых восстановления давления особое влияние оказывают границы пласта, нарушение геометрии потока в призабойной зоне скважины, приток жидкости в скважину после ее остановки и нарушение режима работы скважины перед ее остановкой. К их числу можно отнести и неизотермическое восстановление давления.
Перечисленные факторы искажают кривые восстановления давления и затрудняют их интерпретацию. В то же время при соответствующей интерпретации таких кривых появляется возможность оценки неоднородности пласта и типа коллектора, характера фильтрации и неньютоновских свойств флюида, емкостных характеристик и выявление участия матрицы трещиновато - пористого пласта в процессе разработки и т. д.
Границы пласта
Предположение о бесконечности пласта не соответствует действительности. Реальные пласты имеют конечные размеры.
Продолжительность обычных гидродинамических исследований невелика. За время таких исследований границы пласта или совсем не оказывают влияния на форму кривых восстановления давления, или, если и оказывают, оно практически неощутимо. Поэтому применение схемы бесконечного пласта при обычных (в смысле времени) гидродинамических исследованиях скважин вполне допустимо.
Осложнения, связанные со снятием КВД в скважинах механизированного фонда
В отличии от фонтанирующих скважин в скважинах механизированного фонда технология смены режимов, например для ЭЦН фонда имеет следующий вид.
Центробежный электронасос спускают в скважину после очистки забоя от грязи и осадков. После спуска насоса подъемные трубы заполняют до устья жидкостью, закрывают задвижку и только после этого включают двигатель. При работе насоса в нефтяных скважинах газ из затрубного пространства обязательно выпускают в атмосферу или отбирают под некоторым вакуумом.
При работе насоса в течение некоторого периода производительность его может снизиться. Понижение динамического уровня указывает на то, что производительность уменьшилась вследствие образования пробки на забое. Если динамический уровень не понизился, уменьшение производительности могло произойти в результате попадания значительного количества газа. Обычно при этом повышается давление в затрубном пространстве или возрастает производительность после остановки.
В качестве мероприятий против вредного влияния газа на работу насоса увеличивают его погружение под динамический уровень или же устанавливают на приеме газовый сепаратор.
Глу6ина погружения насоса под динамический уровень зависит от содержания в газожидкостной смеси свободного газа и может колебаться в широком диапазоне от 100 до 400 м, а в некоторых случаях значительно ниже.
Режимы сменяются установкой различных штуцеров, регулированием производительности ЭЦН с помощью терристорных преобразователей, регулированием сечения выкидной линии задвижкой или частотой двойных ходов плунжера для скважин оборудованных ШСНУ. Для смены режимов в ЭЦНУ применяют сменные штуцера.
Основной сложностью при определении депрессии, забойного давления в скважинах мех. фонда является правильность их подсчета исходными данными для этого расчета являются: положение динамического и статического уровня, фазовый состав флюида, распределение его фаз по стволу скважины и т.п.
5.3.НЕКОТОРЫЕ ВОПРОСЫ ИССЛЕДОВАНИЯ МЕХАНИЗИРОВАННОГО ФОНДА СКВАЖИН.
Определение положения динамического уровня

Рис.1.25.Общая схема движения газожидкостной смеси в стволе насосной скважины
Целью определения динамического уровня является установление оптимального режима отбора нефти из скважины, на который влияют множество факторов, определение их и являются задачей исследования скважин. Одним из таких факторов является глубина спуска насоса под динамический уровень, которая в основном определяется фазовым составом добываемой жидкости и скоростью отбора. Естественно, что для определения глубины спуска насоса под динамический уровень следует знать положение самого динамического уровня при данном режиме откачки.
Волнометрирование
Наиболее дешевым и технологичным способом исследования механизированных скважин является способ волнометрирования, при котором определяется положение динамического (статического) уровня в скважине, а так же его изменение во время снятия кривой восстановления уровня (КВУ). Для точного определения забойных (пластовых давлений) по уровням необходимо учесть все сложные процессы движения и перераспределения фаз давления и температуры, происходящие в затрубном пространстве выше приема насоса и в колонне скважины от приема до забоя. Точное решение такого рода задач, при наличии хорошей математической модели, возможно только с применением ЭВМ. Но вместе с тем использование различных графических и упрощенных математических зависимостей, построенных по результатам обработки на ЭВМ позволит оперативно, хотя и с меньшей точностью, определить забойные и пластовые давления. На рис. 1.25 показана общая схема движения газожидкостной смеси в стволе насосной скважины.
При создании математических моделей расчета забойного и пластового давлений по замеренному уровню можно выделить следующие основные задачи:
- повышение точности определения динамического уровня в скважине;
- определение плотности газожидкостной смеси (ГЖС) в затрубном пространстве;
- определение плотности ГЖС в интервале прием насоса–забой скважины и определение забойного давления;
- учет перераспределения фаз и температуры в стволе скважины для определения изменения забойного давления во время снятия КВУ и пластового давления.
Задача повышения точности определения динамического уровня в основном сводится к определению точного значения скорости распространения звуковой волны ,в газовой среде затрубного пространства скважин. На промыслах Западной Сибири широкое распространение получили графические зависимости, связывающие скорость распространения звуковой волны и затрубное давление, построенные на основе данных, полученных путем замера уровня в скважинах, оборудованных реперами, при постепенном повышении или понижении давления в затрубном пространстве. Такие графические зависимости в какой-то мере пригодны для месторождений с низким газовым фактором (до 25 м3/м3),т.е. при условии ,что при работе скважины на стационарном режиме не происходит выделение газа у приема насоса.
К тому же при использовании этих графиков не учитывается влияние температуры в затрубном пространстве на скорость звука.
На месторождениях Западной Сибири в основном давление на приеме насоса ниже давления насыщения нефти газом ,поэтому существует постоянная сепарация газа в затрубное пространство. Газ, проходя через столб нефти в затрубном пространстве ,скапливается в объеме выше динамического уровня. В связи с оттоком газа через обратные газовые клапаны, устанавливаемые на устье между затрубным пространством и выкидной линией, а так же из-за неплотности резьбовых соединений устанавливается определенное равновесное сосотояние, при котором в затрубном пространстве от приема насоса до динамического уровня находится газонефтяная смесь, а выше уровня только газ. Состав газа в этом случае в газовой зоне можно принять соответствующим составу газа, выделившемуся при давлении и температуре у приема насоса. Существуют номограммы для расчета скорости звука, по которым можно с достаточной точностью определить значение динамического уровня, однако они неудобны в применении.
Предлагается использовать для определения скорости звука следующую формулу (выражение для скорости звука учитывающее свойства газа):
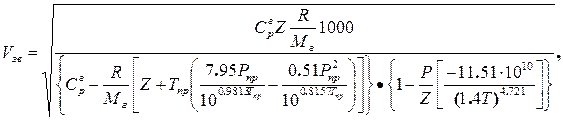
где: Cр – теплоемкость газа при постоянном давлении;
Z – сверхсжимаемость газа при соответствующих Р и Т;
R – газовая постоянная, равная 8.314 кДж/кмоль;
Mг – молярная масса газа, кг/моль;
Тпр – приведенная температура;
Рпр – приведенное давление;
Р – давление в средней части газовой зоны, МПа;
Т – температура в средней части газовой волны,0К.
Использование данной формулы возможно с применением расчетов на ЭВМ, с одновременным расчетом давления и температуры у приема насоса.
5.4.ГИДРОПРОСЛУШИВАНИЕ ПЛАСТОВ
Методы гидропрослушивания пластов
Одним из методов исследования скважин при неустановившемся режиме фильтрации, получившим распространение на промыслах, является метод гидропрослушивания, который позволяет наиболее точно определить фильтрационные свойства пластов на значительном расстоянии от исследуемой скважины. Кроме того, метод гидропрослушивания позволяет качественно и количественно оценивать гидродинамическую связь между скважинами и пластами, а в комплексе с другими методами – оценить неоднородность пласта, выявить литологические экраны и газовые шапки. Метод гидропрослушивания по разновидностям проведения подразделяется на способы: при однократном изменении дебита на постоянную величину и при произвольном изменении дебита; при многократном (гармоническом) изменении дебита.
По способам обработки кривых реагирования они делятся на методы: эталонных кривых, графоаналитические, методы характерных точек и аналитические. Несмотря на такое разнообразие предложенных способов проведения исследований и методов обработки кривых гидропрослушивания на нефтяных промыслах, в основном, ограничиваются однократным импульсированием. Между тем методы многократного изменения дебита имеют ряд преимуществ: строгая периодичность посылки импульсов позволяет легко выделить случайные колебания давления, накладывающиеся на кривую реагирования и увеличить достоверность характерных точек. Метод периодического возбуждения скважин позволяет производить исследования, не нарушая работы промысла в целом, поскольку отпадает надобность в строгом регулировании режимов работы скважины. Основной причиной слабого внедрения этих методов, по-видимому, является несовершенство способов расшифровки кривых реагирования.
Гармонические колебания в пласте могут быть созданы при изменении дебита скважины-источника по закону синуса. Такой режим на практике осуществить довольно трудно. Гораздо легче изменять дебит скважины-источника скачком на постоянную величину, поэтому здесь рассматривается методика исследования по периодическому изменению дебита или так называемая методика импульсного гидропрослушивания.
0сновные понятия о гидродинамических волнах давления в пористой среде
Колебательное движение жидкости является источником волнообразного движения в пласте. Гидродинамические волны давления в пласте подчиняются основным законам волнового процесса, который как любое колебательное движение характеризуется следующими параметрами рис 1.26 данного пункта.
· амплитудой колебаний DРо - наибольшее значение (по модулю) величины возмущения;
· фаза колебаний - мгновенное значение величины возмущения;
· длинна волны 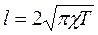 – наименьшее расстояние между двумя одинаковыми состояниями;
– наименьшее расстояние между двумя одинаковыми состояниями;
· период колебаний Т – время между двумя одинаковыми фазами волны;
· частота колебаний w – число колебаний за время одного периода колебаний 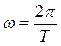 ;
;
·
|
Если в скважине происходит колебание давления по заданному циклу, то каждая гармоническая составляющая колебания их давлений вызывает в пласте соответствующую волну давления.
Исследованиями ряда авторов доказано, что пористая среда является, как бы фильтром гармонических волн давления, который поглощает высокие составляющие спектра сложных периодических циклов. Максимальное расстояние – практически до R=l – достигает только первая гармоническая волна. Все остальные гармонические волны затухают на расстоянии R=l/3 (R – расстояние).
Во всех случаях, независимо от характера колебаний давления в скважине, характер колебаний в пласте на расстоянии R=>1/3 близок к синусоидальному. Амплитуда давлений в произвольной точке пласта зависит от расстоянии между скважинами, параметров пласта, периода и амплитуды колебания дебита и давлений в скважине-источнике. Сдвиг фаз зависит от расстояния между скважинами ,пьезопроводности пласта и частоты колебаний. Таким образом, исследования периодических колебаний давлений для определения параметров пласта основаны на законах распространения первой гармонической волны с периодом равным периоду возмущающего процесса.
Методика гидропрослушивания пористых пластов однократным импульсированием
В настоящее время известна целая группа методов обработки кривых реагирования, полученных при мгновенном однократном изменении дебита возмущающей скважины на постоянную величину .Под мгновенным изменением дебита возмущающей скважины на постоянную величину подразумевается пуск (если скважина простаивала долго) в работу с постоянным дебитом Q, или остановка (если скважина перед этим работала на установившемся режиме),или просто изменение дебита возмущающей скважины на величину Q.
Ниже приводится изложение некоторых широко доступных методов обработки кривых однократного импульсирования.
Метод определения параметров пласта по
точке максимального изменения пластового давления
в реагирующей скважине
Метод В.П. Русских-Ля-Юн-Шаня предполагает, что возмущающую скважину на некоторое время t1=Т/2 пускают в работу с постоянным расходом q0,а затем оставляют. Ясно, что в реагирующей скважине кривая давления будет возрастать, а затем падать до первоначального уровня (см. рис. 1.27).
Таким образом, кривая давления в реагирующей скважине имеет максимум в момент времени Тm .Если бы возмущения в пласте передавались мгновенно, то Тm совпало бы с t1=Т/2 .
Однако ввиду конечной скорости распространения волны давления Тm всегда больше t1, а время задержки (Тm – t1 ), как очевидно тем больше, чем меньше c или больше R. Метод В.П. Русских-Ля-Юн-Шаня и состоит в определении c по известным Тm и t1.
Изменение давления в реагирующей скважине описывается в указанном способе возмущения формулой:
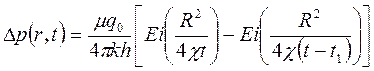 (5.30)
(5.30)
Чтобы найти положение максимума Dpm, выражение (5.30) нужно продифференцировать и приравнять производную нулю. Тогда получим
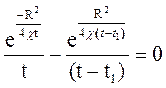
Как только c найдено, аргументы интегрально-показательной функции в (5.30) становятся известными, по значению Dp(Тm) уже легко определяется гидропроводность пласта по формуле:
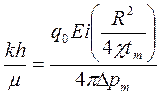 (5.31)
(5.31)
Аналитический метод обработки
кривых реагирования
С.Н.Бузинова и И.Д.Умрихина.
Для того, чтобы сделать более заметным импульс, нужно увеличить t1, а чтобы сделать заметным время задержки Тm–t1, нужно уменьшить t1. Поэтому, желательно иметь такой метод расшифровки опытной кривой в реагирующей скважине, который не был бы основан на времени задержки.
Одним из методов, позволяющих определять параметры пласта не по отдельным точкам, а по характеристикам, вычисленным по всему участку кривой, является аналитический метод Бузинова-Умрихина.
Формула (5.30) в упрощенном в виде для условий бесконечного пласта может быть представлена в виде :
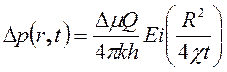 (5.32)
(5.32)
Проинтегрируем уравнение (5.32)
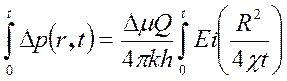 (5.33)
(5.33)
Обозначим:
a= R2(4ct); da= –R2/(4c2t)dt; dt= –R2/(4c2a) da .
Подставляя эти обозначения в (5.33),получаем:
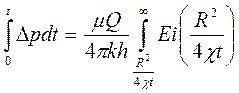 (5.34)
(5.34)
Левая часть выражения (5.34) представляет площадь, ограниченную кривой реагирования и осью абцисс (см. рис 1.27). Разделим (5.34) на Dpt . Тогда имея в виду (5.32) получим:
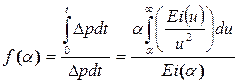 (5.35)
(5.35)

Имея кривую изменения давления в реагирующей скважине, находим площадь, ограниченную этой кривой и осью абцисс. Разделив эту площадь на площадь прямоугольника Dpt (см. рис. 1.27 – б), найдем f(a). И по (рис 1.27 – в) найдем a и Е1(a), и тогда по формуле:
c = R2/(4at) (5.36)
определим пьезопроводность пласта c ,а по формуле:
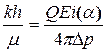 (5.37)
(5.37)
гидропроводность пласта. Иногда для облегчения расчетов коэффициент пьезопроводности может быть найден по номограмме (рис 1.27) .
Этот метод дает удовлетворительные результаты, если кривая реагирования имеет гладкий вид. При обработке негладких кривых реагирования функция f(a) может быть определена с некоторыми погрешностями. Дело в том, что знаменатель функции в виде площади прямоугольника зависит от положения точки на кривой реагирования. Если положение точки определено на дефектном участке, то площадь прямоугольника определяется с погрешностью.
Предлагаемый ниже метод обработки свободен от этих недостатков.
«Метод площадей»
Р.И.Медведского и К.С.Юсупова для обработки
кривых однократного импульсирования
Сущность «метода площадей» заключается в использовании всей кривой реагирования в виде отношения площадей первого цикла однократного импульсирования. (см. рис 1.28)
 Покажем вывод расчетных формул этого метода.
Покажем вывод расчетных формул этого метода.
Интегрируя (5.30)и (5.32) имеем:
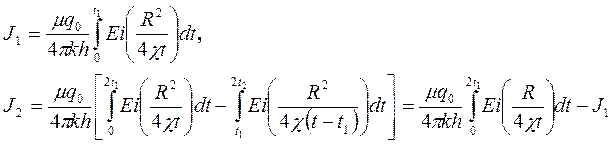
Таким образом
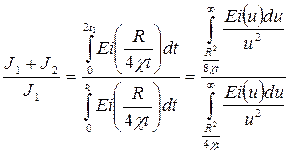 (5.38)
(5.38)
Функция справа зависит только от 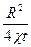 и является универсальной. Таким образом,
и является универсальной. Таким образом, 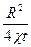 может быть найдено по замеренным J1 и J2. Обозначив функцию, справа через f(a1), где
может быть найдено по замеренным J1 и J2. Обозначив функцию, справа через f(a1), где 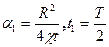 и вычислим отдельно знаменатель формулы (5.38)
и вычислим отдельно знаменатель формулы (5.38)
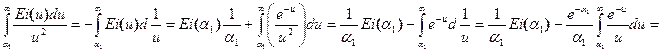
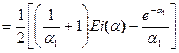
аналогично находим числитель (5.38). Отсюда функция f(a1) выражается более простой формулой
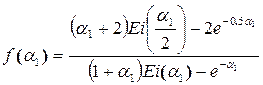 . (5.39)
. (5.39)
Ниже в таблице приведены значения f(a) и Еi(a).Имея кривую реагирования однократного импульсирования по площадям J1 и J2 определяем f(a). По эталонным кривым находим a и тогда по формулам:
c = R2/(4 a1 t1) (5.40)
определим пьезопроводность пласта c ,а по формуле:
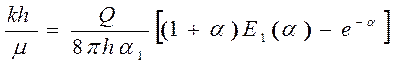 . (5.41)
. (5.41)
Анализ методов обработки однократного импульсирования на
теоретических и практических кривых реагирования
В настоящее время из всех видов гидропрослушивания наибольшее распространение получило однократное импульсирование. Поэтому представляет определенный интерес проверка методов обработки на теоритических кривых прослушивания. Подобная проверка была сделана Р.Г.Шагиевым и В.Г.Крыницким. Однако там не отражены, предложенные в последние годы методы.
Для получения теоретических кривых реагирования используем формулу суперпозиции:
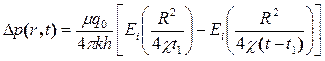
с заранее заданными параметрами: c= см2/c, mq0/4pkh=1, t1=24 ч., расстояние между возмущающей и реагирующей скважинами примем R1=100м, R2=100м, R3=100м,.В результате расчетов получены три кривых гидропрослушивания. Обработав эти кривые предложенными методами для однократного импульсирования имеем:
Сравнительная таблица по методам обработки кривых гидропрослушивания
Дата добавления: 2020-08-31; просмотров: 685;

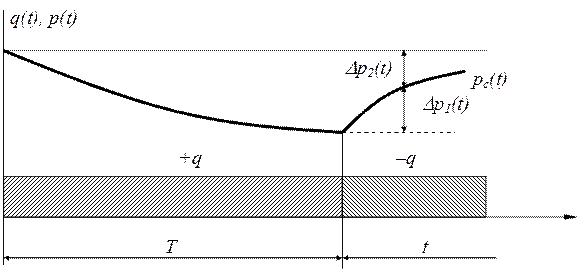 Рис. 1.20.Схема изменения давления в скважине ,вызванного остановкой скважины после работы в течение времени T+t ;T-время работы скважины до остановки
Рис. 1.20.Схема изменения давления в скважине ,вызванного остановкой скважины после работы в течение времени T+t ;T-время работы скважины до остановки
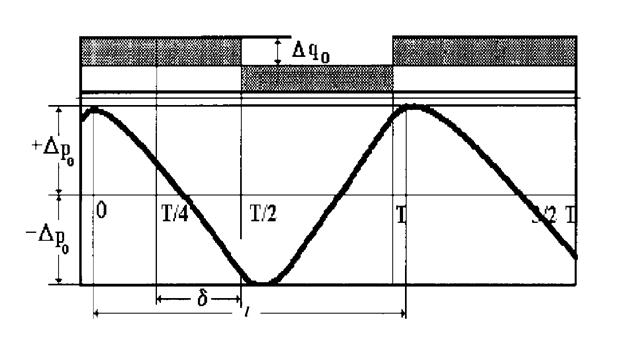 Рис.1.26. Волна давления
Рис.1.26. Волна давления










