Примеры решения задач
Пример 1. Из расчетов на прочность и жесткость определить потребный диаметр вала для передачи мощности 63 кВт при скорости 30 рад/с. Материал вала — сталь, допускаемое напряжение при кручении 30 МПа; допускаемый относительный угол закручивания [φо] = 0,02рад/м; модуль упругости при сдвиге G = 0,8 * 105 МПа.
Решение
1. Определение размеров поперечного сечения из расчета на прочность.
Условие прочности при кручении:

Определяем вращающий момент из формулы мощности при вращении:

Из условия прочности определяем момент сопротивления вала при кручении

Значения подставляем в ньютонах и мм.

Определяем диаметр вала:

2. Определение размеров поперечного сечения из расчета на жесткость.
Условие жесткости при кручении:

Из условия жесткости определяем момент инерции сечения при кручении:
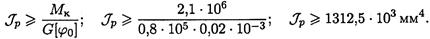
Определяем диаметр вала:
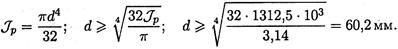
3. Выбор потребного диаметра вала из расчетов на прочность и жесткость.
Для обеспечения прочности и жесткости одновременно из двух найденных значений выбираем большее.
Полученное значение следует округлить, используя ряд предпочтительных чисел. Практически округляем полученное значение так, чтобы число заканчивалось на 5 или 0. Принимаем значение dвала = 75 мм.
Для определения диаметра вала желательно пользоваться стандартным рядом диаметров, приведенном в Приложении 2.
Пример 2. В поперечном сечении бруса d = 80 мм наибольшее касательное напряжение τтах = 40 Н/мм2. Определить касательное напряжение в точке, удаленной от центра сечения на 20 мм.
Решение
Эпюра касательных напряжений в поперечном сечении представлена на рис. 2.37, б. Очевидно,

откуда

 |
Пример 3. В точках внутреннего контура поперечного сечения трубы (d0 = 60 мм; d = 80 мм) возникают касательные напряжения, равные 40 Н/мм2. Определить максимальные касательные напряжения, возникающие в трубе.
Решение
Эпюра касательных напряжений в поперечном сечении представлена на рис. 2.37, в. Очевидно,

Откуда
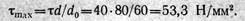
Пример 4. В кольцевом поперечном сечении бруса (d0 = 30 мм; d = 70 мм) возникает крутящий момент Мz = 3 кН-м. Вычислить касательное напряжение в точке, удаленной от центра сечения на 27 мм.
Решение
Касательное напряжение в произвольной точке поперечного сечения вычисляется по формуле

В рассматриваемом примере Мz = 3 кН-м = 3-106 Н• мм,
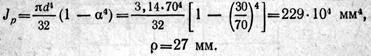
Подставляя числовые значения, получаем

Пример 5. Стальная труба (d0 = l00 мм; d = 120 мм) длиной l = 1,8 м закручивается моментами т, приложенными в ее торцевых сечениях. Определить величину т, при которой угол закручивания φ = 0,25°. При найденном значении т вычислить максимальные касательные напряжения.
Решение
Угол закручивания (в град/м) для одного участка вычисляется по формуле

тогда

В данном случае


Подставляя числовые значения, получаем

Вычисляем максимальные касательные напряжения:

 Пример 6. Для заданного бруса (рис. 2.38, а) построить эпюры крутящих моментов, максимальных касательных напряжений, углов поворота поперечных сечений.
Пример 6. Для заданного бруса (рис. 2.38, а) построить эпюры крутящих моментов, максимальных касательных напряжений, углов поворота поперечных сечений.
Решение
Заданный брус имеет участки I, II, III, IV, V (рис. 2. 38, а). Напомним, что границами участков являются сечения, в которых приложены внешние (скручивающие) моменты и места изменения размеров поперечного сечения.
Пользуясь соотношением

строим эпюру крутящих моментов.
Построение эпюры Мz начинаем со свободного конца бруса:

для участков III и IV


для участка V

Эпюра крутящих моментов представлена на рис, 2.38, б. Строим эпюру максимальных касательных напряжений по длине бруса. Условно приписываем τшах те же знаки, что и соответствующим крутящим моментам. На участке I

на участке II

на участке III

на участке IV

на участке V
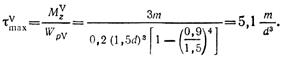
Эпюра максимальных касательных напряжений показана на рис. 2.38, в.
Угол поворота поперечного сечения бруса при постоянных (в пределах каждого участка) диаметре сечения и крутящем моменте определяется по формуле

Строим эпюру углов поворота поперечных сечений. Угол поворота сечения А φл = 0, так как в этом сечении брус закреплен.


Эпюра углов поворота поперечных сечений изображена на рис. 2.38, г.
Пример 7. На шкив В ступенчатого вала (рис. 2.39, а) передается от двигателя мощность NB = 36 кВт, шкивы А и С соответственно передают на станки мощности NA = 15 кВт и NC = 21 кВт. Частота вращения вала п = 300 об/мин. Проверить прочность и жесткость вала, если [τKJ = 30 Н/мм2, [Θ] = 0,3 град/м, G = 8,0-104 Н/мм2, d1 = 45 мм, d2 = 50 мм.
 Решение
Решение
Вычислим внешние (скручивающие) моменты, приложенные к валу:

где
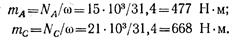
Строим эпюру крутящих моментов. При этом, двигаясь от левого конца вала, условно считаем момент, соответствующий NА, положительным, Nc — отрицательным. Эпюра Mz показана на рис. 2.39, б. Максимальные напряжения в поперечных сечениях участка АВ

что меньше [тк] на

Относительный угол закручивания участка АВ

что значительно больше [Θ] ==0,3 град/м.
Максимальные напряжения в поперечных сечениях участка ВС

что меньше [тк] на

Относительный угол закручивания участка ВС

что значительно больше [Θ] = 0,3 град/м.
Следовательно, прочность вала обеспечена, а жесткость — нет.
Пример 8. От электродвигателя с помощью ремня на вал 1 передается мощность N = 20 кВт, С вала 1 поступает на вал 2 мощность N1 = 15 кВт и к рабочим машинам — мощности N2 = 2 кВт и N3 = 3 кВт. С вала 2 к рабочим машинам поступают мощности N4 = 7 кВт, N5 = 4 кВт, N6 = 4 кВт (рис. 2.40, а). Определить диаметры валов d1 и d2 из условия прочности и жесткости, если [τKJ = 25 Н/мм2, [Θ] = 0,25 град/м, G = 8,0-104 Н/мм2. Сечения валов 1 и 2 считать по всей длине постоянными. Частота вращения вала электродвигателя п = 970 об/мин, диаметры шкивов D1 = 200 мм, D2 = 400 мм, D3 = 200 мм, D4 = 600 мм. Скольжением в ременной передаче пренебречь.
Решение
Нарис. 2.40, б изображен вал I. На него поступает мощность N и с него снимаются мощности Nl, N2, N3.
 Определим угловую скорость вращения вала 1 и внешние скручивающие моменты m, m1, т2, т3:
Определим угловую скорость вращения вала 1 и внешние скручивающие моменты m, m1, т2, т3:

 |
Строим эпюру крутящих моментов для вала 1 (рис. 2.40, в). При этом, двигаясь от левого конца вала, условно считаем моменты, соответствующие N3 и N1, положительными, а N — отрицательным. Расчетный (максимальный) крутящий момент Nx1 max = 354,5 H*м.
Диаметр вала 1 из условия прочности

Диаметр вала 1 из условия жесткости ([Θ], рад/мм)

Окончательно принимаем с округлением до стандартного значения d1 = 58 мм.
Частота вращения вала 2

На рис. 2.40, г изображен вал 2; на вал поступает мощность N1, а снимаются с него мощности N4, N5, N6.
Вычислим внешние скручивающие моменты:

Эпюра крутящих моментов для вала 2 показана на рис. 2.40, д. Расчетный (максимальный) крутящий момент Мя max" = 470 H-м.
Диаметр вала 2 из условия прочности

Диаметр вала 2 из условия жесткости

Окончательно принимаем d2=62 мм.
Пример 9. Определить из условий прочности и жесткости мощность N (рис. 2.41, а), которую может передать стальной вал диаметром d = 50 мм, если [тк] = 35 Н/мм2, [ΘJ = 0,9 град/м; G = 8,0* I04 Н/мм2, n = 600 об/мин.
 Решение
Решение
Вычислим внешние моменты, приложенные к валу:

где

Расчетная схема вала показана на рис. 2.41, б.
На рис. 2.41, в представлена эпюра крутящих моментов. Расчетный (максимальный) крутящий момент Mz = 9,54N. Условие прочности

откуда
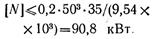
Условие жесткости

откуда
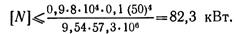
Лимитирующим является условие жесткости. Следовательно, допускаемое значение передаваемой мощности [N] = 82,3 кВт.
Дата добавления: 2020-08-31; просмотров: 850;











