Классификация задач принятия решений

Одно из наиболее важных условий сокращения затрат времени и сил при поиске решения — это умение правильно выбрать метод поиска. За время существования теории принятия решений для наиболее часто встречающихся задач были разрабо­таны методы, учитывающие их характерные особенности.

Практически любая ситуация, требующая принятия решения, может быть отнесена к тому или иному известному классу, и исследователю остается только «узнать» ее. Для этого требуется, по крайней мере, иметь представление о характерных призна­ках различных классов. В настоящее время отсутствует единая универсальная клас­сификационная схема задач принятия решений, однако практически во всех изда­ниях, посвященных этим вопросам, фигурируют следующие классификационные признаки:

- число лиц, принимающих решение;

- вид показателя эффективности;

- степень определенности информации о проблемной ситуации;

- зависимость характеристик проблемной ситуации от времени.

По признаку числа ЛПР различают задачи индивидуального и группового принятия решений. При групповом выборе решений определяющую роль играет проблема со­гласования индивидуальных предпочтений членов группы.

По виду показателя эффективности задачи принятия решения подразделяют на за­дачи со скалярным и векторным показателем.

При использовании скалярного ПЭ предполагается, что ЛПР интересует только одна из составляющих результата операции (то есть только одна из характеристик страте­гии), например, ее длительность. Это наиболее простой случай при выборе стратегии. Но простота не означает, что определить значение скалярного ПЭ тоже легко. Прак­тически все методы математического программирования предназначены для поиска решений именно по скалярному показателю. Необходимо отметить, что при использо­вании этих методов в роли показателя эффективности выступает целевая функция.

При сравнении стратегий по векторному ПЭ могут быть использованы специальные методы, позволяющие свести векторный показатель к скалярному.

Вообще же выбор показателя эффективности является одним из наиболее важных и сложных этапов поиска решения и требует от исследователя не только опыта и зна­ния рассматриваемой предметной области, но и элементов творчества.

По степени определенности информации о проблемной ситуации различают задачи принятия решений в условиях определенности и задачи принятия решений в усло­виях неопределенности.

Задачи принятия решений (ПР) в условиях определенности характеризуются нали­чием полной и достоверной информации о проблемной ситуации, целях, ограниче­ниях и последствиях принимаемых решений. В таких задачах заранее, до начала опе­рации, известно, к какому исходу приведет каждая из стратегий. Это, в частности, означает, что все внешние факторы известны, учтены, и они не могут каким-либо непредвиденным образом повлиять на исход операции.

Характерная особенность всех задач ПР в условиях неопределенности состоит в том, что исход операции зависит не только от стратегий ЛПР и фиксированных факто­ров, но и от неопределенных факторов, не контролируемых ЛПР и не известных ему в момент принятия решения (или недостоверно известных). В результате каждая стратегия оказывается связанной с множеством возможных исходов операции, что существенно осложняет процесс выработки решения.

Задачи принятия решений в условиях неопределенности подразделяют на задачи стохастической и нестохастической неопределенности.

В случае стохастической неопределенности каждой стратегии соответствует неко­торое конечное множество исходов, причем исследователю известны их вероятност­ные характеристики. Но даже если он ориентируется на наиболее вероятный исход, это не означает, что операция будет развиваться именно по данному сценарию. Поэтому задачи такого типа называют также принятием решений в условиях риска. Они имеют место в тех случаях, когда на исход операции могут повлиять те или иные случайные факторы. Например, если встречаются две примерно равные по силам футбольные команды, то возможны три различных исхода матча (либо побеждает первая команда, либо вторая, либо встреча заканчивается вничью); вероятность каждого из исходов известна (равна '/₃), но какой именно будет реализован, остает­ся загадкой практически до окончания игры.

Задачи ПР в условиях нестохастической неопределенности подразделяются, в свою очередь, на задачи ПР в условиях природной и поведенческой неопределенности.

Такие задачи возникают в тех случаях, когда ЛПР не располагает вероятностными характеристиками возможных исходов операции, либо они вообще не являются случайными. В лучшем случае известны лишь диапазоны их значений.

Если ограниченность информации обусловлена недостаточной изученностью при­роды рассматриваемых явлений, то говорят о задачах с «природной» неопределен­ностью.

Если же недостаток информации обусловлен влиянием на ход операции других субъектов помимо ЛПР, то имеет место задача «поведенческой» неопреде­ленности. Для решения задач с поведенческой неопределенностью используются методы теории игр.

По характеру зависимости проблемной ситуации от времени различают статиче­ские и динамические задачи ПР. В динамических задачах параметры (характеристи­ки) проблемной ситуации изменяются во времени.

Классификация задач ПР по перечисленным признакам приводит к различным комбинациям типов задач.

Предпочтения ЛПР могут быть выражены посредством выбора показателя и крите­рия эффективности. В простейшем варианте каждой стратегии может быть поставлено в соответствие значение скалярного ПЭ (здесь применимы методы математического программиро­вания). Более сложная (и более распространенная на практике) ситуация возникает, когда каждая из допустимых стратегий характеризуется векторным ПЭ. Трудности выбора еще более возрастают в условиях неопределенности, при отсутствии однозначного соответствия между стратегиями и их векторными оценками.

Если система предпочтений ЛПР обладает свойствами полноты и направленности, то может быть построена модель предпочтений ЛПР. Слово «модель» в данном случае означает формализованное описание соответствующих категорий, которое обеспе­чивает повторение процедуры выбора в однотипных ситуациях при различных ис­ходных данных. Кроме того, модель предпочтений ЛПР может быть использована для автоматизации процесса поиска решения.

Но в любом случае для успешного решения задачи выбора необходимо выявить и измерить предпочтения ЛПР.

Под выявлением предпочтений ЛПР понимают процесс получения информации о суждениях ЛПР относительно возможных исходов операции.

Существует два подхода к выявлению предпочтений:

- на основе информации о ранее принятых решениях (при многократном повторе­нии выбора в неизменных условиях);

- до принятия решения ЛПР — посредством специальной процедуры опроса.

Именно в результате выявления предпочтений ЛПР оказывается возможным опре­делить, обладают ли они (предпочтения) свойствами полноты и направленности.

Система предпочтений ЛПР обладает свойством полноты на множестве D элементов выбора, если она позволяет сравнить между собой любые два элемента 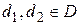и вынести одно из трех альтернативных суждений:

a) 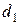предпочтительнее ;

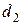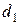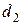б) и равноценны;

в) 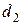предпочтительнее .

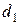Свойство направленности означает следующее. Если, например, при сравнении эле­ментов 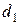и 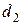ЛПР выносит суждение: « 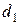предпочтительнее 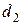», а при сравнении элементов 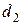и 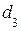— « 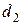предпочтительнее 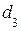», то при сравнении элементов 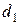и 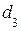его вывод должен быть однозначен: « 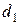предпочтительнее ».

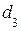Измерение предпочтений есть отображение альтернативных вариантов решений на числовую ось.

В случае описания стратегий с помощью скалярного ПЭ измерение предпочтений не вызывает трудностей. Иногда может быть получена функциональная зависимость между частными ПЭ и результатом операции, что позволяет представить результат в виде скалярной величины.

В более сложных случаях используются другие способы измерения предпочтений. Прежде чем перейти к их описанию, введем понятие «шкалы измерений».

Шкала измерений — есть система обозначений, позволяющая поставить в соответ­ствие объекту некоторый признак и использовать его в дальнейшем для сравнения объектов между собой.

Наибольшее распространение получили номинальные, порядковые и метрические шкалы.

Номинальная шкала (или шкала наименований) – это, по существу, качественная шкала. Ее применяют для обозначения принадлежности объектов к определен­ным классам. Она позволяет описать отношение эквивалентности и различия между объектами. Однако предпочтение между объектами и между классами не устанавливается. Числа в этой шкале используются только для обозначения класса объектов. Пример применения номинальной шкалы — номер цеха или про­изводственного участка на предприятии.

Порядковая (ранговая) шкала — применяется для измерения упорядоченности объектов по одному признаку или по их совокупности. Числа в ней задают толь­ко порядок следования объектов, но не позволяют определить, насколько один объект предпочтительнее другого. Примерами применения ранговой шкалы явля­ются: распределение мест в эстафетной гонке (когда интерес представляет только порядковый номер на финише, а не разница во времени); назначение приорите­тов заявкам, поступающим на обслуживание в вычислительную систему, и т. д.

Метрические шкалы являются наиболее совершенными. На практике применя­ются следующие их виды.

Шкала интервалов используется для описания различия свойств объектов в виде разности. Измерения в данной шкале позволяют определить, насколько один объект лучше другого. При этом обязательно задаются масштаб измере­ний и начало отсчета. В шкале интервалов измеряются, например, сроки вы­полнения различных работ, гарантийные сроки службы устройств, объем затрат на проведение операции.

Шкала отношений — частный случай шкалы интервалов при выборе нулевой точки отсчета. Она является более совершенной, поскольку позволяет определять не только разность, но и отношение между значениями ПЭ. Показате­ли, измеренные в шкале отношений, наиболее распространены в технике и математике. К ним относятся, например, длина, масса, напряжение.

Абсолютную шкалу принято считать наиболее совершенной. В этой шкале используется нулевая точка отсчета и единичный масштаб. Это означает, что измерения в ней могут быть произведены единственным способом (в отличие, например, от шкалы отношений). В абсолютной шкале определяется, в частности, количество объектов (предметов, событий), которое может быть измерено единственным образом с помощью ряда натуральных чисел. Абсолютными являются, например, шкала температур по Кельвину, шкала значений вероятности события.

Рассмотрим некоторые виды показателей эффективности, наиболее часто используемые на практике. Выбор конкретной формы ПЭ во многом зависит от спо­соба описания исхода операции:

а) цель операции описывается случайным событием 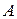, наступление которого явля­ется желательным результатом (целью) операции. Вероятность наступления это­го события 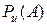зависит от стратегии 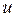. В этом случае ПЭ есть вероятность на­ступления события 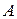, т.е. .

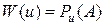б) часто операция считается успешной, если ее результат лежит в некотором за­данном диапазоне. В этом случае рассматри­ваемое событие 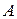заключается в истинности соотношения ;

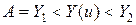в) соответствующий ПЭ трактуется как вероятностная гарантия выполнения по­ставленной задачи: 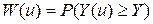. Такой показатель может быть использован для оценки эффективности рассматриваемой операции с точки зрения сроков ее проведения: в качестве Y выступает заданная длительность выполнения работ, а в качестве 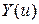— реальные затраты времени;

г) если цель операции выражается числовой переменной, зависящей от случайных факторов, то может быть использован показатель среднего результата: 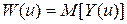. Примерами таких показателей являются среднее число обслуженных заявок, сред­няя длина очереди и т. д. Зная диапазон изменения ПЭ, Вы можете сравнивать значение среднего результата с граничными (допустимыми) значениями результата операции.

Выбор стратегии значительно усложняется, если исход операции оценивается с помощью векторного ПЭ (или множества скалярных ПЭ). Это объясняется тем, что некоторое решение может превосходить остальные по одним показателям и уступать им по другим. В таких условиях трудно определить, которая из стратегий более предпочтительна, не говоря уже об ее оптимальности. Если в задачах принятия решения (ПР) по скалярному показателю основная сложность состоит в разра­ботке или выборе метода поиска экстремума, то в задачах ПР по векторному показа­телю главное внимание уделяется выработке решающего правила, основанного на компромиссе между значениями компонент векторного показателя.

Таким образом, сложность проблемы ПР по векторному показателю даже в условиях определенности связана не столько с трудностями вычисления, сколько с обо­снованностью выбора «наилучшего» решения. Невозможно строго математически доказать, что выбранное решение является наилучшим: любое решение из числа не улучшаемых одновременно по всем показателям может оказать­ся наилучшим для конкретного ЛПР в конкретных условиях. Это является основ­ной аксиомой ПР по нескольким показателям.

В зависимости от способа формирования решающего правила, методы ПР по век­торному показателю можно условно разделить на две группы. К первой группе отно­сятся эвристические методы, в которых ЛПР определяет вид свертки компонент векторного ПЭ в скалярный на основе «здравого смысла» (или интуиции).

Методы второй группы — аксиоматические — основаны на использовании дополнительной информации о компонентах векторного ПЭ.

Рассмотрим некоторые эвристические методы.

а) Метод обобщенного показателя.

Если, исходя из характера задачи, можно допустить, что абсолютное уменьшение одного из показателей компенсируется суммарным абсолютным увеличением дру­гих (показатели однородные), то в качестве обобщенного показателя может быть принята сумма вида:

,

где 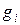— коэффициент относительной важности частного показателя , 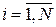- количество частных показателей.

В ряде случаев допустимой считается не абсолютная, а относительная компенсация измене­ния одних показателей другими.

Например, при оценке эффективности функционирования автосалонов фирмы могут быть использованы два частных показателя — математическое ожидание (МО) числа проданных автомобилей 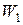и МО не распроданных :

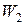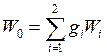
б) метод «затраты/эффект».

Если из существа задачи следует, что одни показатели желательно увеличивать, а другие уменьшать, то в качестве обобщенного ПЭ целесообразно использовать следующее отно­шение:

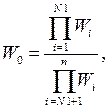
здесь 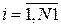— номера показателей, значения которых желательно увеличивать;

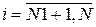— номера показателей, значения которых желательно уменьшать.

Первая группа показателей, как правило, отождествляется с целевым эффектом, а вторая — с затратами на его достижение. При этом показатели не обязательно должны быть однородными.

в) метод целевого программирования.

Основой метода является свертывание частных ПЭ в обобщенный показатель, име­ющий смысл расстояния до «идеальной точки» в пространстве значений показателя эффективности. В качестве «идеальной» обычно выбирают точку, отвечающую представлениям ЛПР об идеальном исходе операции.

В этом случае вычисляется следующим образом:

Здесь 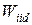— идеальное значение частного ПЭ .

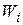В качестве ситуации, иллюстрирующей применение данного подхода, рассмотрим выбор одного из двух мест работы, каждое из которых характеризуется величиной зарплаты ( 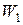), длительностью отпуска ( 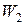) и временем, затрачиваемым на дорогу ( 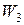). Если выбирающий определил для себя желаемое значение для каждого из этих показателей (соответственно 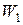, 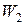и 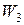), то обобщенный ПЭ будет выглядеть так:

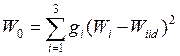
В этом случае будет выбрано такое место работы, для которого отклонение реальных характеристик от желаемых является наименьшим.

г) метод главного показателя.

Если ЛПР считает, что целевой эффект достижим в основном вследствие увеличе­ния одного («главного») частного ПЭ, то исходная задача может быть сведена к зада­че оптимизации по этому показателю при условии, что значения остальных будут не ниже заданных.

Общим недостатком перечисленных методов является зависимость принимаемых решений от некоторых эвристических допущений, задаваемых ЛПР, поэтому эти решения могут не обеспечить действительно лучшей стратегии. Их достоинство — относительная простота реализации.

В тех случаях, когда невозможно произвести свертку векторного ПЭ, необходимо использовать один из аксиоматических методов.

Эти методы основаны на использовании понятия Парето-оптимальности (по фамилии итальянского экономиста В. Парето). Стратегия называется Парето-оптимальной (эффективной), если она по всем показателям не хуже любой стратегии из допусти­мого множества и лучше хотя бы по одному из них (при взаимной независимости частных ПЭ). Чтобы выбрать одну из нескольких эффективных стратегий, необхо­димо располагать дополнительной информацией. Эта информация должна позво­лить ЛПР упорядочить частные ПЭ по их важности, после чего могут быть использо­ваны методы свертки.

Контрольные вопросы и задачи

15.1. Что такое показатель эффективности и как он отражает результат проведения операции?

15.2. Дайте определение критерия эффективности.

15.3. Назовите и кратко охарактеризуйте основные концепции рационального поведения ЛПР.

15.4. Назовите основные классификационные признаки задач принятия решения.

15.5. Дайте определение Парето-оптимальной стратегии.

Глава 16

Оптимальное планирование