ГЛУБИННОСТЬ ИССЛЕДОВАНИЯ
Геометрический фактор характеризует представительность цилиндрических объемов различного радиуса R по величине их относительного вклада в результирующие показания (независимо от конкретной решаемой задачи), поэтому знание радиального изменения G(R) позволяет определить геометрическую глубинность исследования.
Геометрическая глубинность исследования («радиус исследования») R*(Z) есть радиус такого цилиндрического объема, из которого поступает определенная доля, например 90% или 95%, всего регистрируемого на зонде Z излучения (см. рис. 58,б); величина R*(Z) определяется непосредственно через геометрический фактор
G(R*;Z)= 0,9. (9.203)
Геометрическая глубинность изучалась экспериментально и теоретически в связи с задачей определения размеров цилиндрических моделей пласта, обеспечивающих отсутствие краевых эффектов. Кривые, аналогичные приведенным на рис. 58,б, нередко называют кривыми глубинности. Для различных ядерно-физических методов эти кривые имеют форму кривых насыщения, которые, однако, заметно различаются по величине геометрической глубинности (рис. 59).
На рис. 60 показана зависимость радиуса исследования ННМт от размера зонда для обсаженной скважины (dc=197 mm, dкол = 127 мм), заполненной водой, и пластов с водонасыщением 1 и 20 %, вычисленная по декрементной интерпретационной модели (9.203), в сравнении с результатами расчетов по методу Монте-Карло [22,23]. Расхождение с данными аналитического расчета наблюдается только для сравнительно больших зондов, где погрешность расчетов по методу Монте-Карло уже велика.
Выполненные расчеты показывают, что радиус исследования существенно зависит от размера зонда, водородосодержания пласта (изменение хлоросодержания, учитываемое в ННМт, влияет слабо), диаметра, конструкции и заполнения скважины, диаметра глубинного прибора, а также спектра нейтронного источника.
Наряду с понятием геометрической глубинности целесообразно рассматривать понятие «информационной глубинности» исследования, которая измеряется радиусом цилиндрического объема, изменение свойств исследуемой среды вне которого на заданную величину вызывает изменение показаний прибора, превышающее погрешность измерений.
Общее определение информационной глубинности исследования [16] таково: пусть I(R; х1, x2 = x1+∆x) — показание прибора, определяемое параметрами двух сред x1 и xz, из которых первая заключена в цилиндрическом слое толщиной R—rс (соосном со скважиной), вторая — вне этого цилиндра. Если ∆I(R; x1, x2) — изменение показаний прибора, вызванное заданным возмущением ∆x, то информационной глубинностью исследования (радиусом исследования) по параметру х называется такое значение Rε (x, ∆х), при котором
∆I(Rε, x1, ∆x)=kε, (9.204)
где ε — заданная погрешность измерений, k — параметр надежности.
Информационный радиус исследования зависит от свойств пласта, параметра, для определения которого применяется данный метод, от конструкции скважины и прибора, от стабильности и эффективности регистрирующей аппаратуры и мощности источника. Непосредственно через фактор G эта величина не выражается. Важнейшими примерами информационной глубинности являются впервые введенные А.В.Золотовым понятия «глубинность исследования по хлору» и «глубинность исследования по водороду».
Понятие информационной глубинности проиллюстрируем на практически важном примере глубинности исследования по хлору, определенной по результатам математического моделирования методом Монте-Карло (рис. 61). Следуя И.Л.Дворкину, радиусом исследования по хлору назовем разность R—rс, где R — радиус зоны проникновения пресного фильтрата глинистого раствора в пласт, насыщенный минерализованной водой, rс —радиус скважины, при условии, что показания ННМт в пласте с пресным проникновением отличаются от показаний в пласте, полностью насыщенном пресной водой, на величину погрешности измерений.
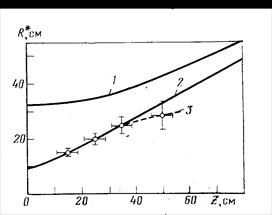 Рис.9.6. Геометрический радиус исследования ННМт как функция размера зонда в обсаженной скважине, заполненной водой. Расчет методом Монте-Карло (по данным И. Л. Дворкина и В. Н. Старикова).
dс=197 мм, dкол,=127 mm, dпр = 42 мм, источник Ро—Be. Вода в скважине, цементе и пласте - пресная. 1 — т=1%; 2 — m=20 %; 3 — m=20 %.
Рис.9.6. Геометрический радиус исследования ННМт как функция размера зонда в обсаженной скважине, заполненной водой. Расчет методом Монте-Карло (по данным И. Л. Дворкина и В. Н. Старикова).
dс=197 мм, dкол,=127 mm, dпр = 42 мм, источник Ро—Be. Вода в скважине, цементе и пласте - пресная. 1 — т=1%; 2 — m=20 %; 3 — m=20 %.
| 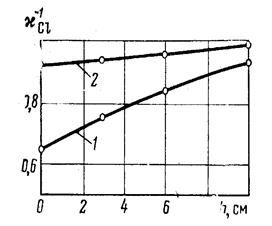 Рис.9.7. Зависимость коэффициента дифференциации показаний ННМт по хлору от глубины проникновения h пресной жидкости в пласт, насыщенный минерализованной водой (по И. Л. Дворкину и др., расчет методом Монте-Карло).
Размер зонда Z=25 см, dc = 197 мм, dкол= 127 мм„ dпр =42 мм, источник Ро—Be.
Рис.9.7. Зависимость коэффициента дифференциации показаний ННМт по хлору от глубины проникновения h пресной жидкости в пласт, насыщенный минерализованной водой (по И. Л. Дворкину и др., расчет методом Монте-Карло).
Размер зонда Z=25 см, dc = 197 мм, dкол= 127 мм„ dпр =42 мм, источник Ро—Be.
|
Расчеты выполнены для двух случаев: скважина сухая, (соответствует прибору, наружный диаметр которого -близок к внутреннему диаметру обсадной колонны) (рис. 61, кривая 1) и скважина заполнена водой (соответствует измерениям прибором малого диаметра) (рис. 61, кривая 2). Коэффициент дифференции показаний по хлору χCl представляет собой отношение показаний NH в пласте, насыщенном соленой водой, к показаниям NB в пласте с зоной проникновения пресной воды, в зависимости от глубины проникновения h = R—rc. Приняв погрешность измерений ε = 5 %, по кривым рис. 61 можно определить, что в скважине, заполненной водой, радиус исследования по хлору составляет всего 3—5 см, а в сухой скважине — около 10 см. Поскольку радиус исследования по хлору определяется длиной диффузии тепловых нейтронов, а радиус исследования по водороду — и длиной замедления, и длиной диффузии, второй значительно больше первого.
Из-за увеличения погрешности измерений с ростом размера зонда информационный радиус исследования как функция Z имеет максимум [84].
Дата добавления: 2020-08-31; просмотров: 761;











