Порядок виконання роботи

1. Ознайомитися із устроєм штангенциркуля та мікрометра.

2. Виконати вимір розмірів деталі за допомогою вимірювального інструмента.

3. Накреслити ескіз деталі із зазначенням необхідних розмірів. Для вала креслити один вид. Указати діаметри всіх ділянок валів. Довжини ділянок вала вказувати від базової поверхні. Для втулки – один вид з розрізом. Вказати зовнішні та внутрішні діаметри й довжини всіх ділянок втулки. Зразок ескізів наведений на рис. 1.4.

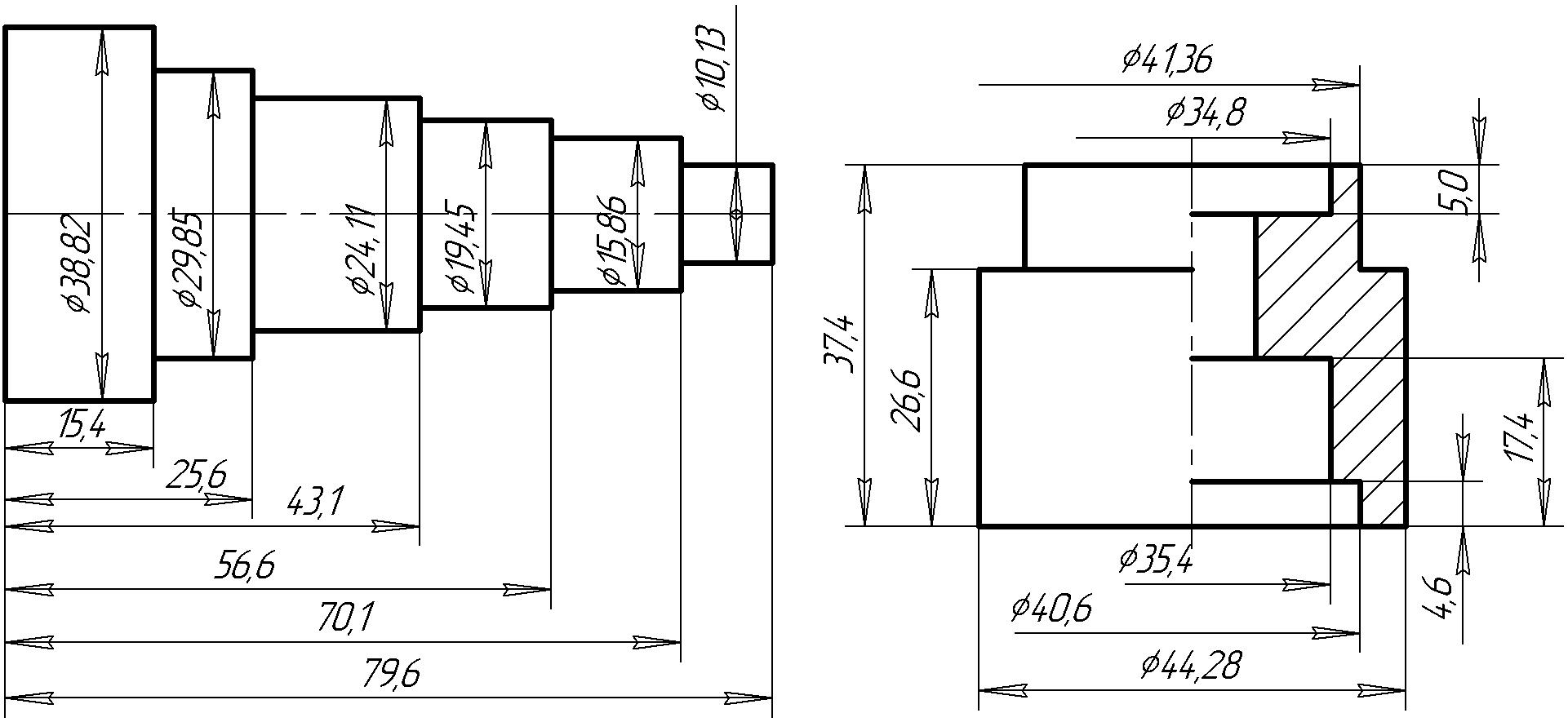
Рис. 1.4. Зразок ескізів вала і втулки

Звіт з лабораторної роботи

Ескіз деталі із зазначенням всіх, необхідних для виготовлення, розмірів.

1.7. Контрольні питання

1. Технічні виміри. Класифікація.

2. Устрій штангенциркуля. Призначення основних деталей.

3. Призначення допоміжної шкали. Ціна розподілу ноніуса.

4. Устрій мікрометра. Призначення основних деталей.

5. Встановити на вимірювальному інструменті значення розміру, зазначене викладачем.

6. Визначити значення розміру, установлене викладачем на вимірювальному інструменті.

Список літератури

1. Якушев А.И. и др. Взаимозаменяемость, стандартизация и технические измерения: Учебник для втузов – 6-е издание, перераб. и дополн. – М.: Машиностроение.–1987.– С. 109-118.

ЛАБОРАТОРНА РОБОТА №2

ДОСЛІДЖЕННЯ ВЗАЄМОЗВ'ЯЗКУ НАВАНТАЖЕННЯ ТА ДЕФОРМАЦІЇ СТРИЖНЯ

Мета роботи

Експериментальна перевірка закону Гука.

Устаткування та матеріали

Експериментальна установка, пустотілий болт із вуглецевої сталі Ст. 3.

Теоретична частина

Працездатність конструкційних матеріалів, які сприймають різні навантаження, обумовлюється геометричними розмірами виробу і їх механічних властивостей. Знання механічних особливостей матеріалу дає можливість конструкторові при проектуванні та розрахунку деталей машин і елементів конструкцій на міцність, а також для призначення матеріалу, з якого їх треба виготовити, установити межу безпечної експлуатації.

Механічні властивості матеріалів визначають експериментально в лабораторних умовах на зразках, форма та розміри яких встановлені відповідними стандартами.

Механічні дослідження мають велике значення не тільки для розрахунків на міцність, але й для контролю якості нових матеріалів, перевірки відповідності їх механічних властивостей вимогам стандартів.

За результатами механічних досліджень розтяганням можна передбачити поведінку матеріалів при стиску, зсуві, згині, крутінні. Для матеріалів і сплавів найбільш інформативним дослідженням є випробування на розтягання (стиск) при статичному навантаженні. Дослідження виконують на зразках круглого, іноді прямокутного перетину (рис. 2.1).

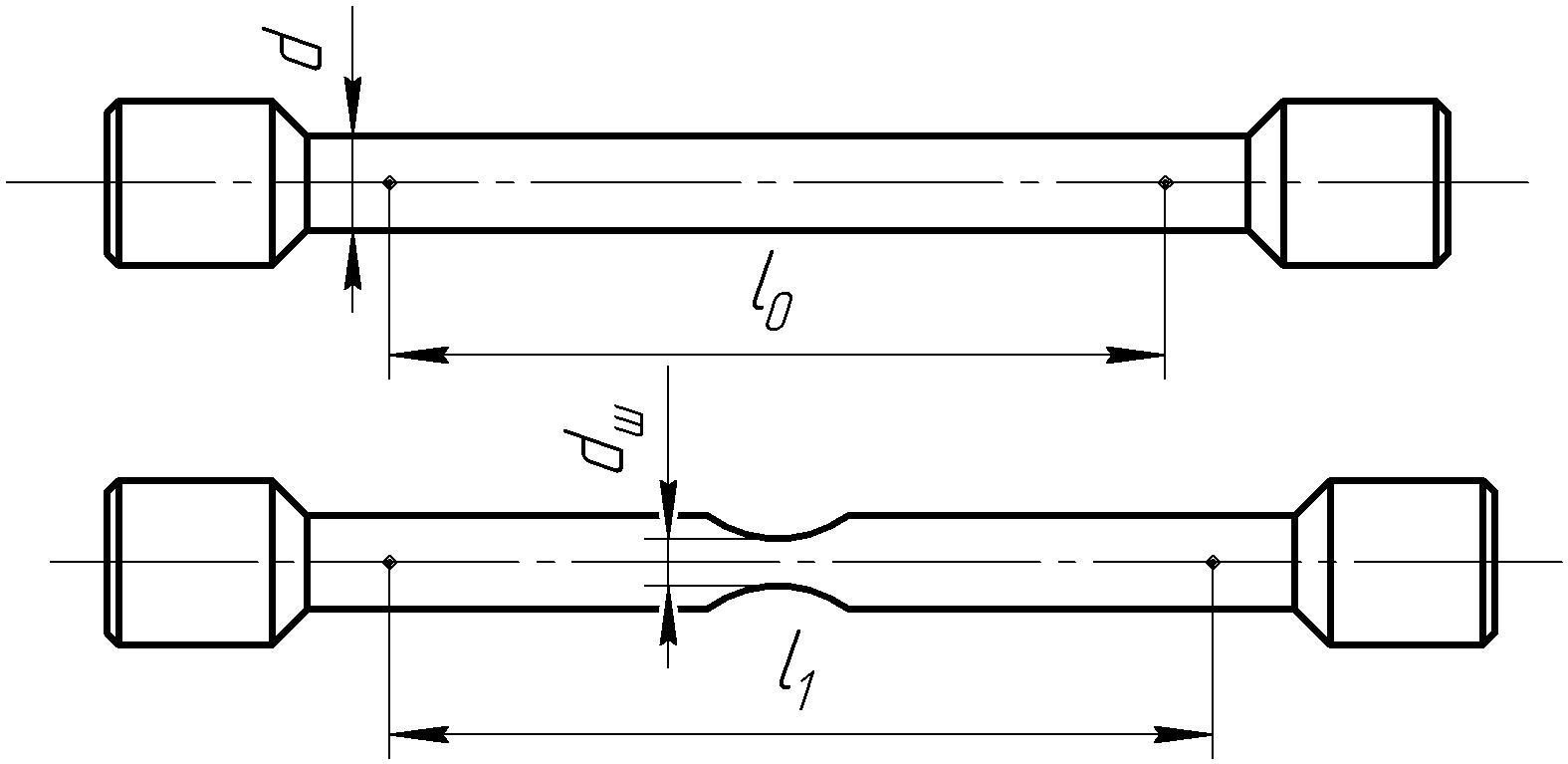
Рис. 2.1. Ескіз стандартного зразка для випробування матеріалів на розтягання

Механічні випробування виконують на універсальних машинах, які оснащені динамометром і пристроєм для автоматичного запису діаграм розтягання в координатах сила – абсолютне подовження (F–Dℓ), що називають діаграмою розтягання (рис. 2.2)

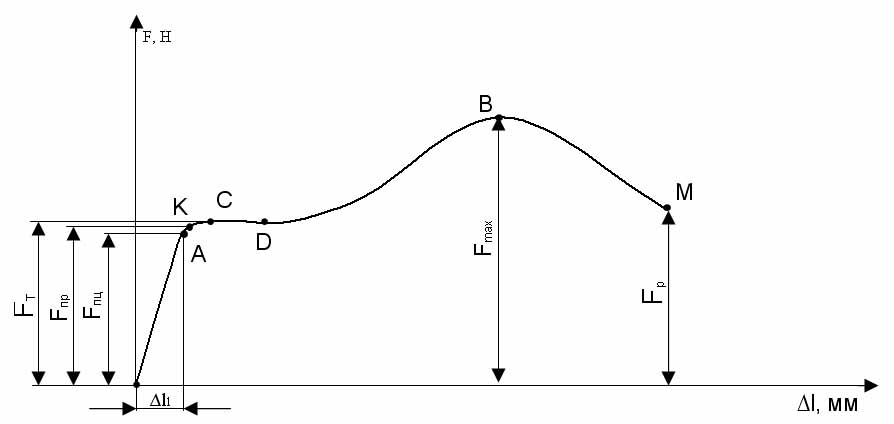
Рис. 2.2. Діаграма розтягання F – Dℓ

Абсолютним подовженням називають збільшення довжини зразка:

,

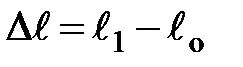де ℓ₀ – початкова довжина;

ℓ₁ – довжина після деформації.

Діаграма розтягання F – Dℓ характеризує властивості конкретного зразка, тому що залежить від його розмірів. Чим більша довжина зразка, тим більше його абсолютне подовження при однаковому навантаженні. Щоб діаграми розтягання не залежали від розмірів зразка, а характеризували властивості матеріалу, на осі ординат відкладають напруження:

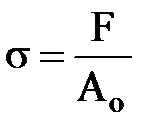, (2.1)

де А₀ – площа поперечного перерізу зразка до випробування.

На осі абсцис відкладають відносне подовження:

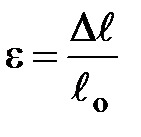, (2.2)

де Dℓ – абсолютне подовження зразка при навантаженні.

Оскільки величини А₀ й ℓ₀ постійні, то діаграма s – e (рис. 2.3.) буде мати такий же вигляд, як і діаграма F – Dℓ і відрізнятися від неї тільки масштабами.

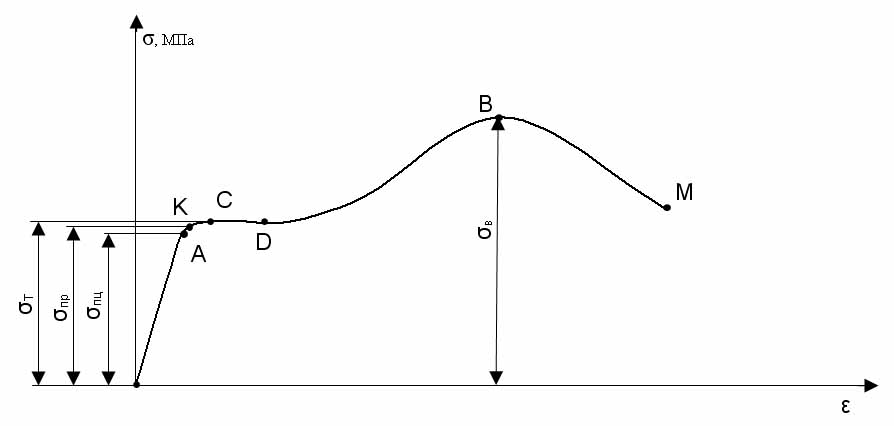
Рис. 2.3. Діаграма розтягання s – e

На діаграмі розтягання показані характерні точки, які відображають стан зразка в різні моменти випробування. Її умовно розділяють на чотири зони.

Перша зона (ділянка ОА) відповідає пружним деформаціям матеріалу зразка, величина яких прямопропорційна силі, що розтягує. Найбільше напруження, для якого справедливий закон Гука, називається межею пропорційності:

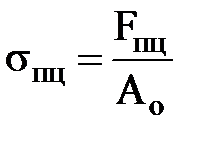. (2.3)

Напруження в точці К є границею пружності – найбільше напруження, до досягнення якого в зразку вже виникають пластичні деформації, але вони ще дуже малі (до 0,02 %):

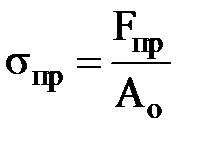. (2.4)

Друга зона (ділянка KD) називається зоною плинності. Тут відбувається подовження зразка без збільшення напруження. Напруження, при якому відбувається збільшення пластичних деформацій зразка, називається межею плинності:

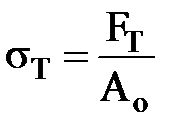. (2.5)

Третя зона (ділянка DB) називається зоною зміцнення. Подовження зразка відбувається більш інтенсивно зі збільшенням навантаження. Умовне напруження, що відповідає найбільшому навантаженню, яке може витримати зразок до руйнування, називається межею міцності:

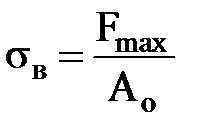. (2.6)

Четверта зона (ділянка BM) називається зоною місцевої плинності або зоною руйнування. Подовження зразка відбувається зі зменшенням сили й виникненням місцевого звуження – шийки. При цьому середнє напруження в поперечному перерізі шийки зростає й у точці М зразок руйнується.

Пластичність матеріалів вимірюють величиною відносного подовження d і відносного звуження y при руйнуванні та визначають за формулами:

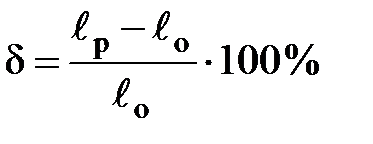, (2.7)

де ℓ_Р – довжина зразка після розриву;

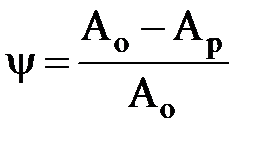, (2.8)

де А_Р – площа поперечного перерізу шийки після розриву.

У цій лабораторній роботі ми будемо досліджувати поведінку матеріалу на ділянці ОА, оскільки експлуатація деталей машин й елементів конструкцій обмежена межею пропорційності, тобто в зоні чинності закону Гука.

В 1676 році Гук експериментально встановив, що в межах пружної деформації абсолютне подовження прямо пропорційне прикладеній силі, початковій довжині стрижня й обернено пропорційне його площі поперечного перерізу, модулю пружності матеріалу, м:

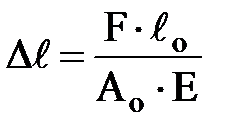, (2.9)

де F – сила, що розтягує зразок, Н;

Е – модуль пружності (коефіцієнт пропорційності), Н/м² (Па).

Ця формула визначає подовження зразка постійного перетину, що розтягується силою F.

Визначимо відносну поздовжню деформацію e у довільній точці стрижня, для чого обидві частини формули 9 розділимо на ℓ₀:

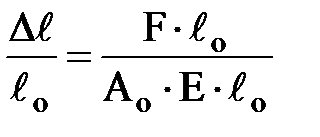. (2.10)

Тоді в лівій частині отримаємо відносну поздовжню деформацію e, а в правій замінимо 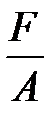на s. Остаточно маємо:

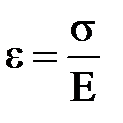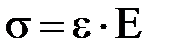або . (2.11)

Нормальне напруження при розтяганні (стиску) прямо пропорційне відносній поздовжній деформації – загальний запис закону Гука.