Способы отбора единиц из генеральной совокупности

В зависимости от задач статистического исследования и специфики объекта изучения используют разные виды, методы и способы отбора единиц в выборку.

1) по виду различают:

1.1. Индивидуальный отбор. Отбор в выборку отдельных единиц генеральной совокупности.

1.2 Групповой отбор. Отбор в выборку единиц из групп, на которые разбита генеральная совокупность.

1.3. Комбинированный отбор. Сочетание двух выше указанных видов.

2) по методу отбора единиц:

2.1. Бесповторный отбор. Отбор, при котором попавшая в выборку единица не возвращается в генеральную совокупность, из которой производится дальнейший отбор.

2.2 . Повторный отбор. Попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в генеральную совокупность для участия в дальнейшей процедуре отбора.

3) по способу отбора единиц:

3.1. Собственно случайная выборка. Выборочная совокупность формируется в результате случайного отбора единиц из генеральной совокупности. При этом объем выборки n определяется обычно, исходя из принятой доли выборки W.

3.1.1. средняя ошибка повторной собственно случайной выборки:

,

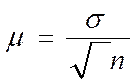где s - среднее квадратическое отклонение.

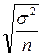- эта ошибка показывает, какие возможны отклонения характеристик выборки от соответствующих характеристик генеральной совокупности.

3.1.2. средняя ошибка бесповторной собственно случайной выборки:

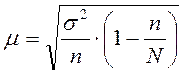
3.1.3. Предельная ошибка выборки:

,

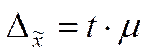где t- коэффициент доверия, - дает возможность выяснить, в каких пределах находится величина генеральной средней.

Таблица 3 - Значение коэффициента доверия

В экономических расчетах рекомендуется использовать доверительную вероятность 0,954 и t, равный 2.

3.2. Механическая выборка – применяется в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. наблюдается определенная последовательность в расположении единиц.

Пример: номера домов и квартир, табельные номера работников и т.д. При этом устанавливается пропорция отбора, т.е. соотнесение объемов выборочной и генеральной совокупностей, например:

N=500 000

n=100 000

100 000/500 000=1/5,

т.е. для исследования отбирается каждая пятая единица, такая выборка является 20%-ной.

Для определения средней ошибки механической выборки используют формулу, как для бесповторной собственно случайной выборки:

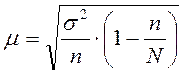
3.3. Типический отбор – используется в тех случаях, когда генеральную совокупность можно разбить на несколько типических групп.

Пример: при обследовании населения такими группами могут быть регионы, республики, края, возрастные группы и др., при исследовании предприятий - отрасль, подотрасль или форма собственности.

При таком способе отбора выборка формируется из каждой типической группы, собственно случайным или механическим способом. Т.о., в выборку в той или иной пропорции попадают представители каждой типической группы.

3.4. Серийный отбор – удобен в тех случаях, когда единицы совокупности объединены в небольшие группы, - серии.

В качестве таких серий можно рассматривать упаковки с определенным количеством продукции, партии товара, бригады, студенческие группы и т.д. Сущность серийной выборки заключается в том, что в выборку серии отбираются собственно случайным или механическим способом, а затем каждая серия подвергается сплошному обследованию.

Серийный отбор часто используется при контроле качества готовой продукции.

3.5 Комбинированный отбор. Его сущность - сочетание рассмотренных выше способов.

Пример: комбинируют серийный и собственно случайный отбор, при этом серии могут отбираться механически, а внутри каждой серии собственно случайный отбор единиц для исследования.

Например, при контроле качества продукции отбирают каждую 20-ю упаковку, а из каждой упаковки в случайном порядке n-ое количество единиц для обследования.

Таблица 4 - Определение необходимого объема выборки

Способ отбора	Повторный	Бесповторный
Собственно-случайный и механический     Типический   Серийная выборка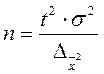

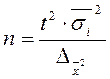
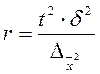
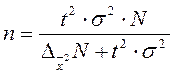
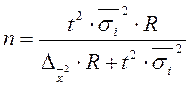
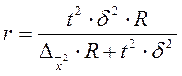
где 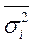- средняя дисперсия из внутригрупповых;

R –число групп при типической или число серий при серийной выборке в генеральной совокупности;

r – число серий в выборке;

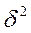- дисперсия межсерийная.