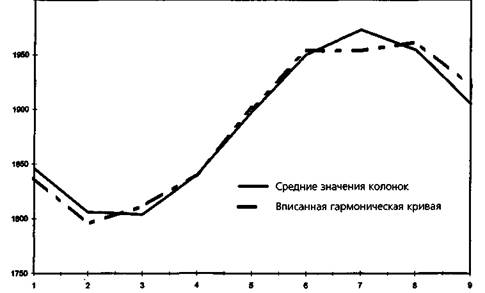
ГАРМОНИЧЕСКАЯ КРИВАЯ, СООТВЕТСТВУЮЩАЯ СРЕДНИМ ЗНАЧЕНИЯМ КОЛОНОК ПЕРИОДОГРАММЫ

ных в предыдущих точках). По этой причине тест Бартелса хорошо под­ходит, в частности, для проверки ценовых данных, которые являются коррелированными рядами.

F-коэффициент.В общем случае в статистике F-коэффициент — это отношение двух дисперсий. Дисперсия — это квадрат стандартного отклонения, которое является мерой волатильности данных. Ряды дан­ных, где точки сильно разбросаны, будут иметь высокое стандартное отклонение и дисперсию. И наоборот, ряды данных, где точки распо­ложены близко к своим средним значениям, будут иметь низкое стан­дартное отклонение и дисперсию.

В циклическом анализе F-коэффициент — это отношение диспер­сии средних значений колонок периодофаммы к дисперсии средних значений строк периодофаммы. Если цикл такой длины в данных не присутствует, средние значения колонок периодофаммы не будут де­монстрировать заметного разброса (в колонках не будет заметных пи­ков и впадин), как, например, было в случае средних значений колонок в периодофамме с восемью колонками для ежегодных данных по куку­рузе (рис. 16.9). Таким образом, не следовало бы ожидать, что диспер­сия средних значений колонок будет значительно больше, чем диспер-

ГЛАВА 16. анализ циклов фьючерсных рынков 601

сия средних значений строк. Это означает, что F-коэффициент не ока­зался бы существенно больше единицы. Если, с другой стороны, цикл данной длины присутствует в данных, дисперсия средних значений ко­лонок было бы значительно больше, чем дисперсия средних значений строк (предполагая, конечно, что из данных был удален тренд), и F-ко­эффициент был бы существенно больше единицы. Чем выше F-коэффи-ииент, тем меньше вероятность, что цикл может оказаться случайным. F-коэффициент представляет собой прекрасный индикатор, пока­зывающий, насколько вероятно, что цикл окажется прибыльным с точ­ки зрения торговли. Если тест Бартелса и хи-квадрат (обсуждаемый да­лее) выявляют значимость цикла, но у цикла низкий F-коэффициент, что иногда случается, его польза с точки зрения торговли вызывает подо­зрение. F-коэффициент особенно чувствителен к наличию тренда, по­скольку присутствие тренда в данных будет сильно повышать дисперсию средних для строк периодограммы, таким образом снижая F-коэффи­циент. Следовательно, если с данных не была полностью снята направ­ленность, F-тест может показать низкую значимость цикла, даже когда на самом деле цикл очень надежен. Поэтому очень важно полностью удалить тренд до перехода к этому этапу тестирования цикла.

Хи-квадрат.Тест хи-квадрат измеряет надежность фазы (времени) цик­ла, т.е. проверяет, обнаруживается ли у цикла тенденция достигать ми­нимумов и максимумов вовремя. В тесте хи-квадрат каждая фаза цикла (т.е. строки периодограммы) разбиваются на семь равных отрезков, или ячеек, с теоретическим пиком цикла, соответствующим центральной ячей­ке. Затем отмечается ячейка, в которой в действительности располагает­ся пик, и подсчитывается количество максимумов цикла, появляющихся в каждой ячейке. Если цикл стабилен, то наибольшее количество макси­мумов попадет в центральную ячейку и соседние с ней, при этом количе­ство максимумов будет снижаться при удалении ячеек от центра. Таким образом, будет наблюдаться высокий разброс (дисперсия) количества мак­симумов в ячейках. И напротив, если цикла нет, количество максимумов в ячейках будет распределено равномерно, и дисперсия количества мак­симумов в ячейках будет низкой. Если дисперсия количества максимумов в ячейках велика по сравнению с дисперсией, которую следовало бы ожидать при случайном распределении, хи-квадрат тест показывал бы значимость цикла, т.е. низкую вероятность того, что цикл случаен.

Резюме.Тест хи-квадрат измеряет надежность фазы цикла (его вре­мени); F-коэффициент измеряет надежность амплитуды цикла (его фор­мы); тест Бартелса измеряет надежность как фазы, так и амплитуды. Ре­альные циклы должны показывать свою значимость на всех трех стати­стических тестах, т.е. иметь вероятности случайности, меньшие чем 0,05 на каждом тесте.

602 ЧАСТЬ 3. осцилляторы и циклы

Таблица 16.2.