Гармоническая линеаризация.
Назначение метода гармонической линеаризации.
Идея метода гармонической линеаризации была предложена в 1934г. Н. М. Крыловым и Н. Н. Боголюбовым. Применительно к системам автоматического управления этот метод разработан Л. С. Гольдфарбом и Е. П. Поповым. Другие названия этого метода и его модификаций - метод гармонического баланса, метод описывающих функций, метод эквивалентной линеаризации.
Метод гармонической линеаризации - это метод исследования автоколебаний. Он позволяет определять условия существования и параметры возможных автоколебаний в нелинейных системах.
Знание параметров автоколебаний позволяет представить картину возможных процессов в системе и, в частности, определить условия устойчивости. Предположим, например, что в результате исследования автоколебаний в некоторой нелинейной системе мы получили зависимость амплитуды этих автоколебаний А от коэффициента передачи k линейной части системы, показанную на рис.12.1, и знаем, что автоколебания устойчивы.
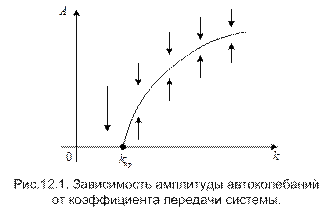
Из графика следует, что при большом значении коэффициента передачи k, когда k > kкр, в системе существуют автоколебания. Их амплитуда уменьшается до нуля при уменьшении коэффициента передачи k до kкр. На рис.12.1 стрелками условно показан характер переходных процессов при разных значениях k: при k > kкр переходный процесс, вызванный начальным отклонением, стягивается к автоколебаниям. Из рисунка видно, что при k < kкр, система оказывается устойчивой. Таким образом, kкр – это критическое по условию устойчивости значение коэффициента передачи. Его превышение приводит к тому, что исходный режим системы становится неустойчивым и в ней возникают автоколебания. Следовательно, знание условий существования автоколебаний в системе позволяет определить и условия устойчивости.
Идея гармонической линеаризации.
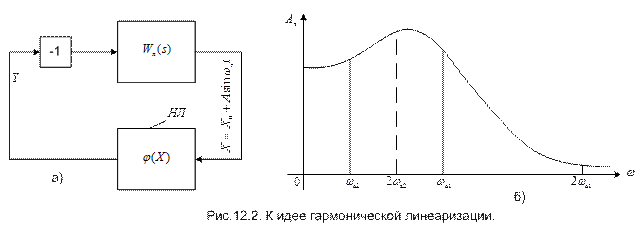
Рассмотрим нелинейную систему, схема которой представлена на рис.12.2, а. Система состоит из линейной части с передаточной функцией Wл (s) и нелинейного звена НЛ с конкретно заданной характеристикой 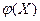 . Звено с коэффициентом - 1 показывает, что обратная связь в системе отрицательна. Полагаем, что в системе существуют автоколебания, амплитуду и частоту которых мы хотим найти. В рассматриваемом режиме входная величина Х нелинейного звена и выходная Y являются периодическими функциями времени.
. Звено с коэффициентом - 1 показывает, что обратная связь в системе отрицательна. Полагаем, что в системе существуют автоколебания, амплитуду и частоту которых мы хотим найти. В рассматриваемом режиме входная величина Х нелинейного звена и выходная Y являются периодическими функциями времени.
Метод гармонической линеаризации основан на nредnоложении, что колебания на входе нелинейного звена являются синусоидальны.ми,т. е. что
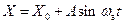 , (12.1)
, (12.1)
гдеА–амплитуда и 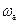 - частота этих автоколебаний , а
- частота этих автоколебаний , а 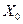 - возможная в общем случае постоянная составляющая, когда автоколебания несимметричны.
- возможная в общем случае постоянная составляющая, когда автоколебания несимметричны.
В действительности автоколебания в нелинейных системах всегда несинусоидальны вследствие искажения их формы нелинейным звеном. Поэтому указанное исходное предположение означает, что метод гармонической линеаризации является принципиально приближенным и область его применения ограничена случаями, когда автоколебания на входе нелинейного звена достаточно близки к синусоидальным. Для того чтобы это имело место, линейная часть системы должна не пропускать высших гармоник автоколебаний, т. е. являться фильтром нижних частот. Последнее иллюстрируется рис. 12.2, б. Если, например, частота автоколебаний равна 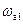 , то линейная часть с показанной на рис. 12.2, б АЧХ
, то линейная часть с показанной на рис. 12.2, б АЧХ 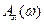 будет играть роль фильтра нижних частот для этих колебаний, так как уже вторая гармоника, частота которой равна 2
будет играть роль фильтра нижних частот для этих колебаний, так как уже вторая гармоника, частота которой равна 2 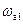 , практически не пройдет на вход нелинейного звена. Следовательно, в этом случае метод гармонической линеаризации применим.
, практически не пройдет на вход нелинейного звена. Следовательно, в этом случае метод гармонической линеаризации применим.
Если частота автоколебаний равна 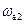 , линейная часть будет свободно пропускать вторую, третью и другие гармоники автоколебаний. В этом случае нельзя утверждать, что колебания на входе нелинейного звена будут достаточно близки к синусоидальным, т.е. необходимая для применения метода гармонической линеаризации предпосылка не выполняется.
, линейная часть будет свободно пропускать вторую, третью и другие гармоники автоколебаний. В этом случае нельзя утверждать, что колебания на входе нелинейного звена будут достаточно близки к синусоидальным, т.е. необходимая для применения метода гармонической линеаризации предпосылка не выполняется.
Для того чтобы установить, является ли линейная часть системы фильтром нижних частот и тем самым определить применимость метода гармонической линеаризации, необходимо знать частоту автоколебаний. Однако ее можно узнать только в результате использования этого метода. Таким образом, пpимeнимocть метода гармонической лuнеарuзацuu прuходuтся определять уже в конце uсследованuя в порядке проверки.
Заметим при этом, что если в результате этой проверки гипотеза о том, что линейная часть системы играет роль фильтра нижних частот, не подтверждается, это не означает еще неверности полученных результатов, хотя, разумеется, ставит их под сомнение и требует дополнительной проверки каким-либо другим методом.
Итак, предположив, что линейная часть системы есть фильтр нижних частот, считаем, что автоколебания на входе нелинейного звена синусоидальны, т.е имеют вид (12.1). Колебания на выходе этого звена будут при этом уже несинусоидальными вследствие их искажения нелинейностью. В качестве примера на рис. 12.3 построена кривая на выходе нелинейного звена для определенной амплитуды входного чисто синусоидального сигнала по характеристике звена, приведенной там же.
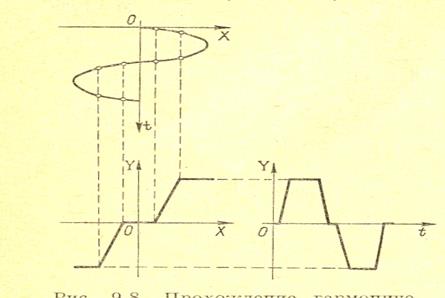
Рис.12.3. Прохождение гармонического колебания через нелинейное звено.
Однако, поскольку мы считаем, что линейная часть системы пропускает только основную гармонику автоколебаний, имеет смысл интересоваться только этой гармоникой на выходе нелинейного звена. Поэтому разложим выходные колебания 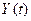 в ряд Фурье и отбросим высшие гармоники. В результате получим:
в ряд Фурье и отбросим высшие гармоники. В результате получим:
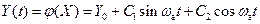 . (12.2)
. (12.2)
Здесь
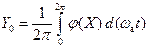 ;
;
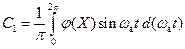 ; (12.3)
; (12.3)
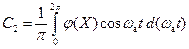 ;
;
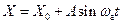 .
.
Перепишем выражение (12.2) в более удобном для последующего использования виде, подставив в него получающиеся из (12.1) следующие выражения для 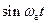 и
и 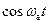 :
:
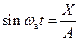 и
и 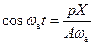 .
.
Подставив эти выражения в (12.2), будем иметь:
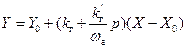 (12.4)
(12.4)
или
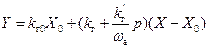 . (12.5)
. (12.5)
Здесь введены обозначения:
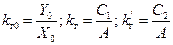 . (12.6)
. (12.6)
Дифференциальное уравнение (12.5) справедливо для синусоидального входного сигнала (12.1) и определяет выходной сигнал нелинейного звена без учета высших гармоник.
Коэффициенты 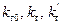 в соответствии с выражениями (12.3) для коэффициентов Фурье являются функциями постоянной составляющей
в соответствии с выражениями (12.3) для коэффициентов Фурье являются функциями постоянной составляющей 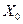 , амплитуды А и частоты
, амплитуды А и частоты 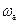 автоколебаний на входе нелинейного звена. При фиксированных А,
автоколебаний на входе нелинейного звена. При фиксированных А, 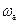 и
и 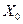 уравнение (12.5) является линейным. Таким образом, если отбросить высшие гармоники, то для фиксированного гармонического сигнала исходное нелинейное звено может быть заменено эквивалентным линейным, описываемым уравнением (12.5). Эта замена и называется гармонической линеаризацией.
уравнение (12.5) является линейным. Таким образом, если отбросить высшие гармоники, то для фиксированного гармонического сигнала исходное нелинейное звено может быть заменено эквивалентным линейным, описываемым уравнением (12.5). Эта замена и называется гармонической линеаризацией.
На рис. 12.4 условно изображена схема этого звена, состоящая из двух параллельных звеньев.
Рис. 12.4. Эквивалентное линейное звено, полученное в результате гармонической линеаризации.
Одно звено (  ) пропускает постоянную составляющую, а другое – только синусоидальную составляющую автоколебаний.
) пропускает постоянную составляющую, а другое – только синусоидальную составляющую автоколебаний.
Коэффициенты 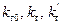 называются коэффициентами гармонической линеаризации или гармоническими коэффициентами передачи:
называются коэффициентами гармонической линеаризации или гармоническими коэффициентами передачи: 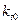 - коэффициент передачи постоянной составляющей, а
- коэффициент передачи постоянной составляющей, а 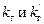 - два коэффициента передачи синусоидальной составляющей автоколебаний. Эти коэффициенты определяются нелинейностью
- два коэффициента передачи синусоидальной составляющей автоколебаний. Эти коэффициенты определяются нелинейностью 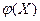 и значениями
и значениями 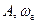 и
и 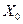 по формулам (12.3). Существуют определенные по этим формулам готовые выражения для
по формулам (12.3). Существуют определенные по этим формулам готовые выражения для 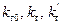 для ряда типовых нелинейных звеньев. Для этих и вообще всех безынерционных нелинейных звеньев величины
для ряда типовых нелинейных звеньев. Для этих и вообще всех безынерционных нелинейных звеньев величины 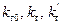 не зависят от
не зависят от 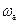 и являются функциями только амплитуды А и
и являются функциями только амплитуды А и 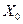 .
.
Постоянная составляющая 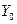 на выходе нелинейного звена (см. уравнения 12.2, 12.4) появляется по одной из двух причин: если к системе приложено внешнее постоянное воздействие, создающее
на выходе нелинейного звена (см. уравнения 12.2, 12.4) появляется по одной из двух причин: если к системе приложено внешнее постоянное воздействие, создающее 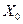 (см. уравнение 12.1), или если характеристика нелинейного звена несимметрична относительно начала координат, вследствие чего происходит явление выпрямления входного синусоидального сигнала.
(см. уравнение 12.1), или если характеристика нелинейного звена несимметрична относительно начала координат, вследствие чего происходит явление выпрямления входного синусоидального сигнала.
При гармонической линеаризации нелинейных звеньев с такими характеристиками нельзя выражать 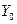 через
через 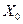 с помощью коэффициента гармонической линеаризации
с помощью коэффициента гармонической линеаризации 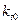 ,т. е. в виде
,т. е. в виде
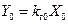 ,
,
так как здесь 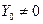 и при
и при 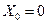 . Поэтому для несимметричных нелинейностей нельзя пользоваться уравнением (12.5), а следует применять уравнение (12.4). Соответствующая схема представлена на рис. 12.4,б.В связи с этим для таких нелинейностей вместо
. Поэтому для несимметричных нелинейностей нельзя пользоваться уравнением (12.5), а следует применять уравнение (12.4). Соответствующая схема представлена на рис. 12.4,б.В связи с этим для таких нелинейностей вместо 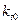 даются выражения непосредственно для
даются выражения непосредственно для 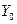 .
.
При отсутствии внешнего воздействия и симметричной характеристике 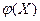 постоянная составляющая
постоянная составляющая 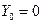 и уравнение (12.4) принимает вид:
и уравнение (12.4) принимает вид:
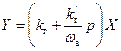 (12.7)
(12.7)
или
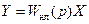 , (12.8)
, (12.8)
где 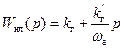 - передаточная функция эквивалентного линейного звена, которую можно назвать гармонической передаточной функцией нелинейного звена.
- передаточная функция эквивалентного линейного звена, которую можно назвать гармонической передаточной функцией нелинейного звена.
Итак, при гармонической линеаризации, нелинейное звено заменяется линейным, эквивалентным для постоянной составляющей входного сигнала и приближенно эквивалентным для его колебательной составляющей. При этом приближенно принимается, что спектр колебательной составляющей входного сигнала состоит из одной гармоники, и пренебрегается ее искажением в нелинейном звене.
Условием применимости метода линеаризации в замкнутой системе является выполнение линейной частью системы роли фильтра нижних частот. Полоса пропускания должна быть мала по сравнению с высшими гармониками автоколебаний.
С помощью гармонической линеаризации можно определить параметры возможных автоколебаний в интересующей нас точке системы, которые могут быть использованы для определения устойчивости нелинейной системы, качества переходных процессов.
Дата добавления: 2016-12-09; просмотров: 9098;











