Методологические основы

Рассмотрим некоторые простейшие теоретические основы, без понимания которых невозможно представить себе, что именно, какие побочные излучения следует ожидать от некого обобщенного сигнала в цепях ПЭВМ.

Напомним, что изначальная постановка задачи «от лица» потенциального противника состоит в том, что он должен решать простейшую бинарную задачу - что передавалось в данный момент, «ноль» или «единица», т.е. задача решается для одного двоичного разряда. При этом предполагается, что потенциальный противник точно знает структуру устройства, алгоритм обработки информации, виды кодирования и т.д.

Исходя из этого, и будем рассматривать модель сигнала и ее предполагаемый спектр.

На рис. 5.18 слева приведен простейший одиночный импульсный сигнал, так называемая «дельта-функция». Такой сигнал характеризуется бесконечно малой длительностью и бесконечной амплитудой, аплощадь такого импульса всегда равен 1. Спектр такого сигнала приведен на том же рисунке справа. Спектр такого сигнала сплошной (без учета свойств случайных антенн в конкретном техническом средстве), бесконечный по частоте и его огибающая плоская.

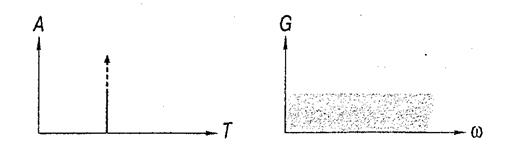
Рис. 5.18. Дельта-функция и ее спектр

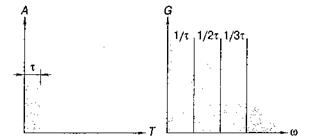
Рис. 5.19. Однократный импульс конечной длительности и его спектр

Однако в реальности таких импульсов не бывает. Приблизим модель к реальности и рассмотрим одиночный импульс конечной длительности (рис. 5.19).

Как видим, огибающая спектра стала неравномерной. На рисунке огибающая представлена по абсолютной величине, в реальности каждый четный лепесток направлен во второй квадрант. Такого рода огибающая спектра описывается простым выражением:

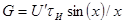(5.10)

Сделаем следующий шаг в приближении модели к реальным сигналам. Рассмотрим бесконечную последовательность импульсов конечной длительности. Такой сигнал и его спектр приведены на рис. 5.20.

Следует обратить внимание, что амплитуда импульсов меньше, чем одиночного импульса на предыдущем рисунке, а амплитуды гармонических составляющих спектра даже выросли. Это не случайное нарушение масштаба. Это, разумеется, только качественное,

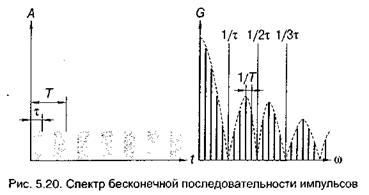
отражение реальности. Это свойство спектра импульсной последовательности лежит в основе существующих методов СИ.

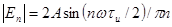(5.11)

Таким образом, спектр последовательности импульсов становится «линейчатым», сохраняя огибающую одиночного импульса («лепестки» огибающей, по-прежнему, имеют «ширину» 1/ 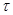. Причем «шаг» гармоник по частоте обратен периоду следования импульсов. А вот амплитуда гармонических составляющих выросла. Именно этот эффект и позволяет резко улучшить соотношение сигнал/шум при измерении сигналов ПЭМИН.

Все приведенные выше спектры иллюстрируют предельно идеализированную картину. Реальные спектры ПЭМИН при совпадении частот составляющих с теорией, имеют абсолютно случайные распределения амплитуд. Нельзя забывать, что реальное излучение есть суперпозиция большого числа излучателей (случайных антенн), у каждого из которых своя амплитудно-частотная характеристика со своими пиками и провалами, резонансами и т.д.

Особо следует отметить следующее. В понимании физики этих процессов есть одна особенность. Практически всегда инженер уверен, что именно такой спектр существует реально, объективно. Мы привыкли априори считать, что наши приборы отражают реальную, объективно существующую картину мира. А ведь это не всегда является истиной. В данном случае «видно» отображение объективной реальности узкополосным, селективным, прибором. И эти частотные составляющие, гармоники, возникают только в нашем средстве измерения.

В реальности существует только сплошной спектр от каждого фронта каждого импульса. Естественно, что он конечен, поскольку конечна длительность фронта. Он неравномерный, поскольку искажен свойствами реальных случайных антенн. Но всегда сплошной!!! А линейчатым он становится только в нашем приемнике, за счет инерционности, своеобразной «памяти» входного устройства, и нигде иначе.

В реальных устройствах импульсные последовательности не бывают бесконечными. Практически без исключений любая пересылка, обработка и т.д. выполняется «пакетами». Поэтому наиболее реальной моделью сигнала в цепях ПЭВМ будет последовательность таких пакетов, в которых длина пакета существенно больше длительности одного импульса. Такая модель и ее спектр представлены на рис. 5.21.

A G

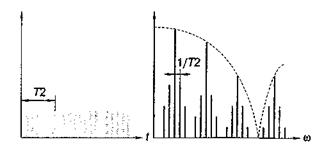
Рис. 5.21. Спектр последовательности пакетов импульсов

Как видно на рисунке (масштаб изображений изменен для наглядности, приведены не все боковые составляющие) около каждой спектральной составляющей, обусловленной самими импульсами, появились боковые составляющие, обусловленные частотой следования пакетов.

Для иллюстрации рассмотрим, например, типовой случай - ПЭМИН видеоподсистемы ПЭВМ. Стандартный тест-режим для СИ этого устройства - вывод на экран видеосигнала, представляющего собой чередование прямоугольных импульсов с такими же по времени промежутками между ними (сигнал типа «меандр»). Каждая строка растра при этом представляет собой пакет импульсов. Число импульсов в пакете равно половине разрешения экрана по горизонтали (для режима 1024-768 это составит 512 импульсов). Далее пауза, обусловленная обратным ходом строчной развертки, и новый пакет.

Участок спектра такого сигнала приведен на рис. 5.22. В левой части экрана одна из гармоник тактовой частоты следования импульсов, правее первая и вторая «верхние» боковые частоты с «шагом», равным частоте строчной развертки дисплея.

Исходя из вышеизложенного, становится понятным, сколь важен режим функционирования исследуемого блока (узла) ПЭВМ. Учитывая, что в составе любого цифрового устройства, одновременно работают десятки схем, узлов, блоков без точного знания того, какие именно частоты нужно искать, проведение СИ невозможно. Каждый из сотен сигналов подчиняется некой тактовой частоте. Эти частоты, как правило, независимы, многие из них делятся и умножаются. И, к сожалению, все они излучают...

Для выделения опасного сигнала, необходимо однозначное знание трех параметров: длительности импульса, частоты их следования в пакете, частоты следования пакетов.

Глава 5

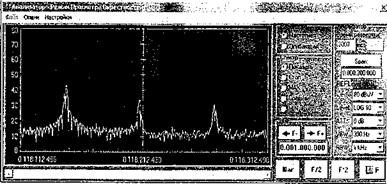
Рис. 5.22. Спектр опасного сигнала от видеоподсистемы. Скрин с экрана системы «Сигурд»

Кроме вышеизложенного, следует напомнить, что это же необходимо еще и для правильного расчета результатов измерений.

Вновь обратим внимание на то, что амплитуды гармонических составляющих для последовательности импульсов значительно больше, чем амплитуда огибающей спектральной плотности для одиночного импульса.

Однако нормами определен расчет параметров защищенности одного импульса, независимо от предыдущих и последующих. Именно поэтому в расчетных формулах присутствует операция деления на корень из частоты следования импульсов. Таким образом, неверное определение этой частоты однозначно дает неверный результат исследования.

Отсюда же следует, что эта величина во время измерений должна быть постоянной. Если тактовая частота во время измерений претерпевает изменения, то:

во-первых, «сдвигаются» со своих мест (по частоте) гармонические составляющие (что же тогда мы измеряем?);

во-вторых, какую частоту подставлять при расчете?

Весьма ограниченный объем настоящего курса не предоставляет возможности подробнее рассмотреть все аспекты организации тест-режима (или выбора из имеющихся рабочих режимов устройства) исследуемой ПЭВМ. Ограничимся результирующим утверждением - выбранный режим должен обеспечивать прохождение по информационным цепям бесконечной (или достаточно длительной по времени) последовательности пакетов импульсов с постоянной тактовой частотой и длительностью (как импульсов, так и их пакетов).

Все перечисленные параметры необходимо знать (или измерить в соответствующих цепях) с достаточной для последующего расчета точностью.