Представление графов

Граф – это множество однотипных объектов (вершин), некоторые из которых связаны друг с другом какими-либо связями (ребрами). Одна связь всегда соединяет только две вершины (иногда – вершину саму с собой). Основные разновидности графов:

· неориентированные (обычные), в которых важен только сам факт связи двух вершин

· ориентированные (орграфы), для которых важным является еще и направление связи вершин

· взвешенные, в которых важной информацией является еще и степень (величина, вес) связи вершин

Примеры графов разных типов:

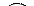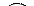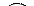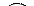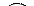
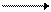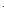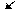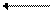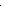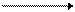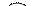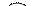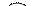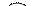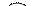
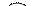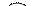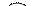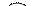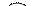
обычный	ориентированный	взвешенный

Для описания графа как структуры данных используются два способа: матрицы смежностиисписки смежности. Первый способ предполагает использование двумерного массива чисел, который для простых графов заполняется только значениями 0 (нет связи) и 1 (есть связь), а для взвешенного – значениями весов. Для обычного графа матрица смежности всегда является симметричной относительно главной диагонали, а для орграфа чаще всего эта матрица не симметрична, что отражает одностороннюю направленность связей.

Для рассмотренных выше примеров матрицы смежности будут следующими:

Недостатки данного способа:

· заранее надо знать хотя бы ориентировочное число вершин в графе

· для графов с большим числом вершин матрица становится слишком большой (например 1000*1000 = 1 миллион чисел)

· при малом числе связующих ребер матрица заполнена в основном нулями

Этих недостатков во многом лишен второй способ, основанный на использовании списков смежных вершин. Здесь списки содержат ровно столько элементов, сколько ребер в графе, и кроме того вершины и ребра могут добавляться динамически. Список смежных вершин представляет собой главный список всех вершин и множество вспомогательных списков, содержащих перечень вершин, связанных с данной. Для рассмотренных выше обычного графа и ориентированного графа списки смежности будут следующими:

B A C A D A E A E D C B E D C B A

E E A D B E A C B E D C B A

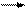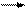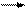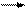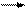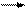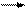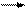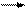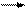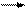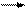
Описание подобной сложной списковой структуры выполняется обычным образом.

Операции добавления и удаления по сравнению с деревьями имеют следующие варианты:

· добавление новой связи (ребра) между заданной парой существующих вершин

· добавление новой вершины вместе со всеми необходимыми связями

· удаление связи (ребра) между двумя вершинами

· удаление вершины вместе со всеми ее связями

Добавление нового ребра включает в себя (на примере обычного графа):

· получение имен связываемых вершин

· поиск в основном списке первой связываемой вершины

· поиск в списке смежных ей вершин второй связываемой вершины и либо вывод сообщения об ошибке, либо добавление в этот список нового элемента с именем второй вершины

· поиск в основном списке второй связываемой вершины

· поиск в списке смежных ей вершин первой связываемой вершины и либо вывод сообщения об ошибке, либо добавление в этот список нового элемента с именем первой вершины

Добавление новой вершины включает в себя:

· запрос имени новой вершины вместе с именами всех связываемых с ней вершин

· поиск в основном списке имени новой вершины и в случае отсутствия ее -добавление в основной список

· формирование списка вершин, смежных вновь добавленной

· поиск в основном списке всех смежных вершин и добавление в их вспомогательные списки нового элемента с именем новой вершины

Удаление ребра производится следующим образом:

· запрос имен двух вершин, между которыми разрывается связь

· поиск в основном списке каждой из этих вершин

· поиск в каждом из двух вспомогательных списков имени соседней вершины и удаление соответствующего элемента

Удаление вершины производится следующим образом:

· запрос имени удаляемой вершины

· поиск ее в основном списке

· просмотр вспомогательного списка удаляемой вершины, для каждого элемента которого:

o поиск смежной вершины в основном списке и удаление из ее вспомогательного списка элемента, соответствующего удаляемой вершине

o удаление самого элемента из вспомогательного списка

· удаление вершины из основного списка

При обработке графов часто приходится выполнять обход всех его вершин. Правила обхода графов похожи на обход деревьев. Существуют два основных правила обхода, известные как поиск в глубину и поиск в ширину.

Поиск в глубину использует две структуры – стек для запоминания еще не обработанных вершин и список для запоминания уже обработанных. Поиск выполняется следующим образом:

· задать стартовую вершину (аналог корневой вершины при обходе дерева)

· обработать стартовую вершину и включить ее во вспомогательный список обработанных вершин

· включить в стек все вершины, смежные со стартовой

· организовать цикл по условию опустошения стека и внутри цикла выполнить:

o извлечь из стека очередную вершину

o проверить по вспомогательному списку обработанность этой вершины

o если вершина уже обработана, то извлечь из стека следующую вершину

o если вершина еще не обработана, то обработать ее и поместить в список обработанных вершин

o просмотреть весь список смежных с нею вершин и поместить в стек все еще не обработанные вершины

Например, для рассмотренного выше обычного графа получим:

· пусть стартовая вершина – B

· включаем B в список обработанных вершин: список = (В)

· помещаем в стек смежные с В вершины, т.е. A и E: стек = (А, Е)

· извлекаем из стека вершину E: стек = (А)

· т.к. E нет в списке обработанных вершин, то обрабатываем ее и помещаем в список: список = (В, Е)

· смежные с E вершины – это A и B, но B уже обработана, поэтому помещаем в стек только вершину А: стек = (А, А)

· извлекаем из стека вершину А: стек = (А)

· т.к. А нет в списке обработанных вершин, то помещаем ее туда: список = (В, Е, А)

· смежные с А вершины – это B, C, D, E, из которых B и E уже обработаны, поэтому помещаем в стек C и D: стек = (A, C, D)

· извлекаем из стека вершину D: стек = (A, C)

· т.к. D не обработана, то помещаем ее в список: список = (B, E, A, D)

· смежные с D вершины – это А и С, из которых А уже обработана, поэтому помещаем в стек вершину С: стек = (А, С, С)

· извлекаем из стека вершину С: стек = (А, С)

· т.к. С не обработана, помещаем ее в список: список = (B, E, A, D, C)

· смежные с С вершины – это A и D, но они обе уже обработаны, поэтому в стек ничего не заносим

· извлекаем из стека С, но она уже обработана

· извлекаем из стека А, но она тоже уже обработана

· т.к. стек стал пустым, то завершаем обход с результатом (B, E, A, D, C)

Поиск в ширину работает немного по другому: сначала обрабатываются все вершины, смежные с текущей, а лишь потом – их потомки. Вместо стека для запоминания еще не обработанных вершин используется очередь. Последовательность действий:

· задать стартовую вершину (аналог корневой вершины при обходе дерева)

· обработать стартовую вершину и включить ее во вспомогательный список обработанных вершин

· включить в очередь все вершины, смежные со стартовой

· организовать цикл по условию опустошения очереди и внутри цикла выполнить:

o извлечь из очереди очередную вершину

o проверить по вспомогательному списку обработанность этой вершины

o если вершина уже обработана, то извлечь из очереди следующую вершину

o если вершина еще не обработана, то обработать ее и поместить в список обработанных вершин

o просмотреть весь список смежных с нею вершин и поместить в очередь все еще не обработанные вершины

Тот же что и раньше пример даст следующий результат:

· пусть стартовая вершина – B

· включаем B в список обработанных вершин: список = (В)

· помещаем в очередь смежные с В вершины, т.е. A и E: очередь = (А, Е)

· извлекаем из очереди вершину А: очередь = (Е)

· т.к. она не обработана, добавляем ее в список: список = (В, А)

· смежные с А вершины – это B, C, D и E, помещаем в очередь вершины C, D и E: очередь = (E, C, D, E)

· извлекаем из очереди вершину Е: очередь = (C, D, E)

· т.к. Е не обработана, помещаем ее в список: список = (B, A, E), т.е. в первую очередь обработаны обе смежные с В вершины

· смежные с Е вершины – это А и В, но обе они уже обработаны, поэтому очередь новыми вершинами не пополняется

· извлекаем из очереди вершину С: очередь = (D, E)

· т.к. С не обработана, то помещаем ее в список: список = (B, A, E, С)

· смежные с С вершины – это А и D, помещаем в очередь только D: очередь = (D, E, D)

· извлекаем из очереди вершину D: очередь = (E, D)

· т.к. D не обработана, помещаем ее в список: список = (B, A, E, С, D)

· смежные с D вершины – это А и С, но обе они обработаны, поэтому очередь не пополняется

· извлекаем из очереди вершину Е, но она уже обработана: очередь = (D)

· извлекаем из очереди вершину D, но она уже обработана и т.к. очередь становится пустой, то поиск заканчивается с результатом (B, A, E, С, D), что отличается от поиска в глубину.

В заключение отметим несколько наиболее часто встречающихся задач на графах:

· найти путь наименьшей (наибольшей) длины между двумя заданными вершинами

· выделить из графа дерево, имеющее наименьший суммарный вес ребер (кратчайшее покрывающее дерево)

· присвоить каждой вершине графа цвет таким образом, чтобы не было ни одной пары смежных вершин, имеющих одинаковый цвет, и при этом число используемых цветов было бы минимальным (задача раскраски графа)

· найти в графе такой путь, который проходит по всем вершинам ровно по 1 разу и имеет при этом наименьшую суммарную длину (задача бродячего торговца или коммивояжера).