Гипоидная и спироидная передачи
Зубчатые передачи со скрещивающимися осями – гиперболоидные, так как их начальные конические поверхности, строго говоря, являются частью гиперболоидов вращения. У гипоидной передачи шестерня обычно является коническим колесом с тангенциальными или круговыми зубьями; у спироидной передачи коническая шестерня–червяк имеет винтовые зубья.
Достоинства гипоидных и спироидных передач заключаются в следующем: валы и их опоры для обоих колес могут быть выведены за пределы передачи в обоих направлениях (рис. 100, з), что исключает консольные нагрузки на валы; передачи характеризуются высокой нагрузочной способностью и плавностью работы.
Характерный недостаток гиперболоидных передач – повышенное скольжение активных поверхностей зубьев, вызванное смещением осей колес, отсюда сравнительно невысокий КПД и склонность к заеданию; такие передачи смазывают специальным противозадирным так называемым гипоидным маслом, содержащим специальные присадки.
Гипоидные передачи широко применяют в автомобилях, тракторах, тепловозах, металлорежущих станках и других машинах. Спироидные передачи вследствие сложности изготовления и низкого КПД распространения не получили.
Конструкция конических колес. На рис. 108 показаны наиболее распространенная в конических редукторах конструкция колес (а) и вала-шестерни (б); насадные колеса небольшого диаметра делают монолитной конструкции (см. выше). Для экономии высококачественной стали применяют бандажированные конструкции колес, у которых зубчатый венец насаживается на колесный центр, изготовляемый из чугуна или стального литья.
В единичном и мелкосерийном производстве колеса небольшого (до 150 мм) диаметра изготовляют из прутков, а большого диаметра из поковок; в крупносерийном и массовом производстве заготовками стальных колес обычно являются штамповки. Чугунные колеса всегда изготовляют отливкой. Стальные колеса большого диаметра (более 500 мм) отливают или делают сварными.
| Передачи с зацеплением Новикова Как известно из теоретической механики и сопротивления материалов, в высших кинематических парах звенья соприкасаются по линиям и точкам, а максимальные контактные напряжения вычисляются по формуле Герца, причем зна-чение контактных напряже-ний зависит от приведен-ного радиуса кривизны поверхностей контакта, – чем больше приведенный ра-диус кривизны, тем меньше максимальные контактные напряжения. Приведенный радиус кривизны равен | 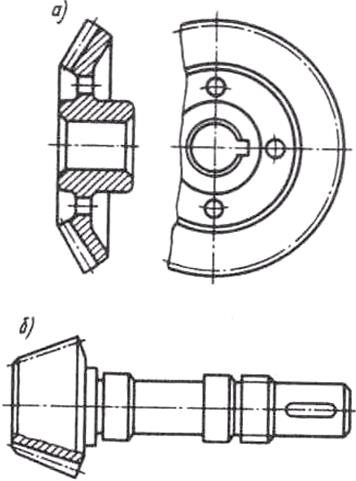 Рис. 108
Рис. 108
|
rпp=r1r2/(r2±r1),
где r1 и r2 – радиусы кривизны в точке касания; знак плюс принимают при центрах кривизны, расположенных по разные стороны от точки контакта (внешнее касание), знак минус – при центрах кривизны, расположенных по одну сторону (внутреннее касание).
Нагрузочная способность цилиндрических и конических передач ограничена из-за малого значения приведенного радиуса кривизна (в формуле для ставится знак плюс), а значит, и значительных контактных напряжений. Инженером М.Л. Новиковым предложено круговое зацепление (рис. 109), в котором зуб одного колеса (обычно шестерни) выпуклый, а другого – вогнутый, причем профили зубьев в нормальном сечении очерчиваются дугами окружностей с небольшой разницей в радиусах, что дает большие значения приведенных радиусов кривизны (в формуле для rпp ставится знак минус) и существенно уменьшает контактные напряжения.
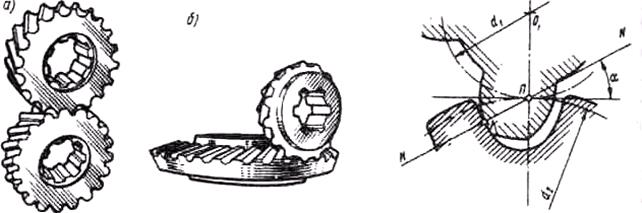
| Рис. 109 | Рис. 110 |
В круговом зацеплении зубьев в нормальном сечении (рис. 110) профили зубьев, очерченные дугами окружностей, не являются сопряженными, так как они не удовлетворяют требованиям основной теоремы зацепления (общая нормаль NN не будет все время проходить через полюс П),следовательно, для обеспечения постоянства передаточного числа передача Новикова должна быть косозубой.
Линия зацепления изображенной на рис. 110 передачи будет проходить через точку K и располагаться параллельно осям колес, а точка контакта зубьев будет перемещаться по этой линии, а не по общей нормали NN,как в эвольвентном зацеплении. Поэтому торцовое перекрытие, а также геометрическое скольжение зубьев в передаче Новикова теоретически отсутствуют, плавность работы обеспечивается за счет осевого перекрытия eb>1,1. Угол наклона зубьев обычно берется в пределах b=10…24°.
Первоначальный точечный контакт зубьев в результате непродолжительной приработки переходит в контакт по значительной площадке, что резко снижает контактные напряжения.
Различают передачи Новикова ОЛЗ (с одной линией зацепления) и передачи Новикова ДЛЗ (с двумя линиями зацепления); в последнем случае профиль зубьев обоих колес выпукло-вогнутый. В передачах ДЛЗ, получивших наибольшее распространение, выпуклые головки шестерни и колеса одновременно взаимодействуют с вогнутыми ножками колеса и шестерни. Очевидно, что при прочих равных условиях нагрузочная способность передач ДЛЗ больше, чем передач ОЛЗ.
Исходный контур и расчет геометрии цилиндрических передач Новикова с двумя линиями зацепления стандартизован; кроме того, для передач с одной и двумя линиями зацепления стандартизованы нормальные модули от 1,6 до 63 мм. Стандарт на расчет геометрии передач Новикова ДЛЗ ограничивает области применения этой передачи значениями: твердость зубьев – не выше 320 НВ, модуль m<16 мм, окружная скорость v – не более 20 м/с. Нагрузочная способность передач Новикова ДЛЗ по условию контактной выносливости активных поверхностей зубьев примерно в два раза выше, чем у передач с эвольвентным зацеплением, а прочность зубьев на изгиб несколько ниже.
К элементам зацепления круговых зубьев различной формы относятся (рис. 111): а – выпуклый зуб (1 – след линии зацепления, 2 – начальная точка контакта, 3 – контактная линия, 4 – площадка контакта); б – вогнутый зуб; в – выпукло-вогнутый зуб.
Габаритные размеры передач Новикова примерно на 25...30% меньше, чем у равноценных эвольвентных.
Основной недостаток передач Новикова – повышенная чувствительность к перекосам осей и изменению межосевого расстояния, поэтому для них требуется высокая точность изготовления колес и высокая жесткость валов и опор.
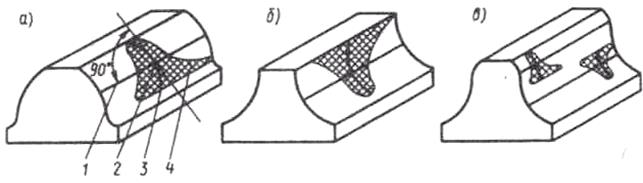
Рис. 111
Дата добавления: 2020-07-18; просмотров: 781;











