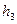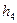Способы подсчета объемов земляных работ
При строительстве сооружений, особенно ирригационных , дорог, подземных коммуникаций, стоимость земляных работ является преобладающей от всей стоимости объекта строительства.
В процессе проектирования преобразования рельефа при вертикальной планировке возникает необходимость вычисления объемов земляных тел, слагающих планируемую территорию и объемов земляных работ по выемке и отсыпке (насыпи). Объем земляного тела определяется для того, чтобы отыскать положение проектной поверхности, соответствующее поставленным техническим условиям. Объем земляных работ необходимо знать для того, чтобы сопоставлять различные варианты проектов преобразования рельефа и определения стоимости земляных работ.
Способы подсчета объемов земляных тел и земляных работ практически одинаковы. Объем земляных тел выполняется по практическим (положительным) отметкам, а объемы земляных работ по рабочим отметкам, которые имеют знак + для отсыпки (насыпи) и знак – для выемки.

| |
| |
| |



ПК 1 ПК 2
Рис. 2.2 Определение объемов земляных тел
Объем вычисляется как интеграл
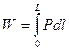 , (2.42)
, (2.42)
где, в соответствии с Рис.2.2, Р- площадь поперечного сечения тела между пикетами и (или) плюсовыми точками, l –пртяженность рассматриваемого участка тела между пикетами и (или) плюсовыми точками, L – общая длина тела (расстояние между ПК 1 и ПК 2).
Сложные формы рельефа земной поверхности не позволяют точно подсчитать объемы земляных тел, поэтому для подсчетов используют математические тела (правильные геометрические фигуры). Все способы определения объемов в зависимости от используемых математических тел можно подразделить на:
1) способ квадратных призм;
2) способ суммирования рабочих отметок центров тяжести квадратов;
3) способ треугольных призм;
4) способ горизонтальных пластов;
5) способ изораб;
6) способ вертикальных профилей.
Общим приемом для всех способов является разбивка земляного тела на правильные геометрические фигуры.
Первый способ разбивкой на квадратные призмы. При этом, площадка линией нулевых работ разбивается на участки выемки и подсыпки (Рис 2.3 Б). В пределах каждого участка выделяют полные квадраты и квадраты разбитые линией нулевых работ на другие фигуры (трапеции, треугольники, пятиугольники). Объем при этом для одной призмы (в пределах целого квадрата, Рис.2.3- а) вычисляется по формуле
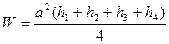 , (2.43)
, (2.43)
где а – сторона квадрата 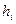 -рабочие отметки.
-рабочие отметки.
|
| ||||
 | |||||





 а) б) А
а) б) А



 Б
Б




|
|



 В
В

 Г
Г
1 2 3 4 5
Рис.2.3 Способ квадратных призм, а) объем земляных работ в пределах одного полного квадрата; б) разбивка линией нулевых работ сетки квадратов на участки выемки (выше линии нулевых работ) и подсыпки ниже линии нулевых работ).
Для всех полных квадратов выемки (подсыпки) объем составит
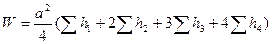 , (2.44)
, (2.44)
Где, подстрочный индекс при рабочей отметке 1,2,3,4 обозначает число вершин квадратов, сходящихся в данной точке.
Существуют несколько разновидностей этого способа, основанных на формулах, предложенных различными авторами, например:
|


 Формула Ньютона- Котеса
Формула Ньютона- Котеса
| |
| |

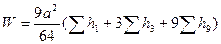 ;
;
| |
(2.45)
|
Рис.2.4
|

| |
| |

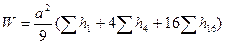 ;
;
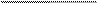
(2.46)
|
Рис.2.5

| |
| |

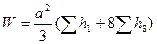 .
.
|
Рис.2.6
На рисунках 2.4- 2.6 представлены данные, поясняющие учет рабочих высот для разных вершин квадратов (цифры обозначают - сколько раз данная рабочая высота участвует в суммировании при вычислении объёмов земляных тел).
Для неполных квадратов объем вычисляется по формуле
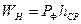 , (2.48)
, (2.48)
где 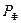 -площадь фигуры, образованной сторонами квадрата и линией нулевых работ,
-площадь фигуры, образованной сторонами квадрата и линией нулевых работ, 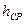 - среднее арифметическое из рабочих отметок этой фигуры.
- среднее арифметическое из рабочих отметок этой фигуры.
Полный объем выемки (или отсыпки) найдется как сумма объемов по полным и неполным квадратам.
Второй способ основан на разбивке земляного тела на квадратные призмы, высота которых равняется 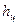 - рабочей отметке центра тяжести квадрата. Объем такой призмы равен
- рабочей отметке центра тяжести квадрата. Объем такой призмы равен
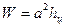 , (2.49)
, (2.49)
где 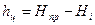 . При этом все квадраты, чей центр тяжести располагается выше линии нулевых работ относится, например к выемке, а ниже к подсыпке или наоборот, в зависимости от знаков рабочих отметок
. При этом все квадраты, чей центр тяжести располагается выше линии нулевых работ относится, например к выемке, а ниже к подсыпке или наоборот, в зависимости от знаков рабочих отметок
Объем насыпи и выемки найдется 
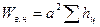 (2.50)
(2.50)
Третий способ основан на разбивке зеленого тела на треугольные призмы ( Рис. 2.7) с вычислением объема земляных работ по каждой призме по формуле
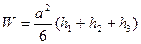 . (2.51)
. (2.51)
а) б)
|





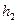











| |  | |






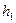
| |||
 | |||
Рис.2.7- Треугольные призмы. а) вид отдельной треугольной призмы; б) площадка разбитая на треугольные призмы
Для площадки объем насыпи или выемки составит
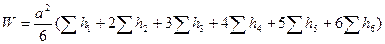 . (2.52)
. (2.52)
Четвертый способ основан на расчленении земляного тела на пласты, ограниченные горизонталями- горизонтальными сечениями, проведенными через определенный интервал – высоту сечения рельефа. На Рис 2.8 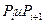 площади смежных сечений, измеренные на плане, например электронным планиметром; h- высота пласта, обычно равна высоте сечения горизонталями
площади смежных сечений, измеренные на плане, например электронным планиметром; h- высота пласта, обычно равна высоте сечения горизонталями
Объем находится по формулам
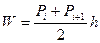 , (2.53)
, (2.53)
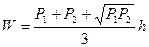 . (2.54)
. (2.54)



Рис.2.8 Способ горизонтальных пластов.
Пятый способ аналогичен четвертому, но вместо горизонталей используются изорабы- линии равных рабочих отметок.
Шестой способ- способ вертикальных профилей ( Рис. 2. 9) применяется при ВП линейных объектов (сооружений).

Рис.2.9 Способ вертикальных профилей.
При незначительном поперечном уклоне объем находится отдельно для выемки и насыпи по формуле
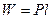 , (2.55)
, (2.55)
где Р- площадь продольного сечения, l-ширина дороги (канала). При поперечных уклонах превышающих 0,2 (причем он неравномерный по трассе), то объем вычисляется для отдельных участков (путем разбивки трассы на участки) по формуле
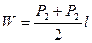 , (2.56)
, (2.56)
где Р1, Р2 – площади смежных поперечных сечений, l- расстояние между ними (Рис.2.8.9). Формулой можно воспользоваться если между точками 1 и 2 нет точки нулевых работ. Если есть точка нулевых работ, то одно из сечений должно быть проведено через точку нулевых работ.
 |  |
Рис.2.10 Смежные поперечные сечения
2.8.2. Картограмма земляных работ.
При подсчете объемов планировочных работ на последней стадии технического проектирования составляется картограмма земляных работ. На ней разными цветами показываются контуры выемки и насыпи. В каждом квадрате указывается объемы земляных работ, отметки земли, проектные и рабочие отметки вершин квадратов. Картограмма передается строителям для перенесения проекта в натуру. Одновременно она служит для учета выполненных земляных работ
2.8.3. Точность определения объемов земляных работ.
Точность подсчета зависит от трех основных факторов, это:
- густота точек с исходными высотами, с которой связана ошибка определения объема за счет обобщения рельефа, по исследованиям В.Д. Большакова ее можно рассчитать по формуле

Рис. 2.11. Подсчет объемов по результатам нивелирования по квадратам
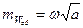 , (2.57)
, (2.57)
где а- сторона квадрата, коэффициент 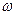 = 0.012 м - точность определения высот исходных точек .
= 0.012 м - точность определения высот исходных точек .
Выведем формулу относительной погрешности определения по способу центров тяжести квадратов
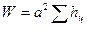 , (2.58)
, (2.58)
Где 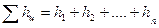 .
.
Продифференцируем выражение (2.58) по всем независимым переменным и получим
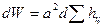 . (2.59)
. (2.59)
Заменим дифференциалы квадратами средних квадратических погрешностей , с учетом того , что
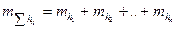 , (2.60)
, (2.60)
при равенстве слагаемых получим
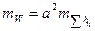 . (2.61)
. (2.61)
Учитывая, что 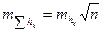 , получим значение
, получим значение
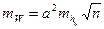 . (2.62)
. (2.62) 
Относительная погрешность определения объёма составит
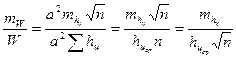 . (2.63)
. (2.63)
Пример для высоты сечения горизонталями равном 0,5 м, 
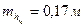 ,
, 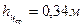 , n=100, получим относительную погрешность определения объёма равной
, n=100, получим относительную погрешность определения объёма равной 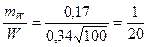 , то есть, 5% от объёма.;
, то есть, 5% от объёма.;
Экспериментально установлено, что наиболее точными способами являются – квадратных и треугольных призм. Примерно такую же точность имеет способ суммирования центров тяжести. Остальные способы менее точные. Предельные ошибки для лучших способов при сетке со стороной в 20 м достигают 10-20%.
Производительность труда по определению объемов земляных работ можно установить путем хронометража.
Дата добавления: 2019-02-08; просмотров: 1484;