Кинематика групп Ассура
При кинематическом анализе механизмов обычно выделяют три задачи: задачу о положениях, задачу о скоростях и задачу об ускорениях.
Эти задачи решаются последовательно, нельзя, например, решить сразу третью задачу, не решив предварительно две первых. Рассмотрим решение трёх задач кинематики для групп Ассура второго класса.
Вводимые обозначения.Рассмотрим рис. 3.1, на котором изображены группы второго класса пяти видов. Каждая группа включает в себя два звена и три кинематические пары. Одно из звеньев группы обозначим номером i, а второе – номером k. Внешние кинематические пары обозначим – B и D, а внутреннюю – C. Для того чтобы группа была кинематически определима, должны быть известны положения, скорости и ускорения внешних кинематических пар в неподвижной системе координат X0Y0Z0. Например, при решении задачи о положениях должны быть известны: для внешних вращательных пар – координаты центров этих пар, для внешних поступательных пар – координаты произвольной точки на оси пары и проекции единичного вектора оси пары. При аналитическом расчете упомянутые координаты и проекции единичных векторов являются входами в группы. Поскольку каждая группа второго класса имеет две внешние кинематические пары и одну внутреннюю, то для каждой группы необходимо задавать два входа. Сведем эти входы в таблицу.
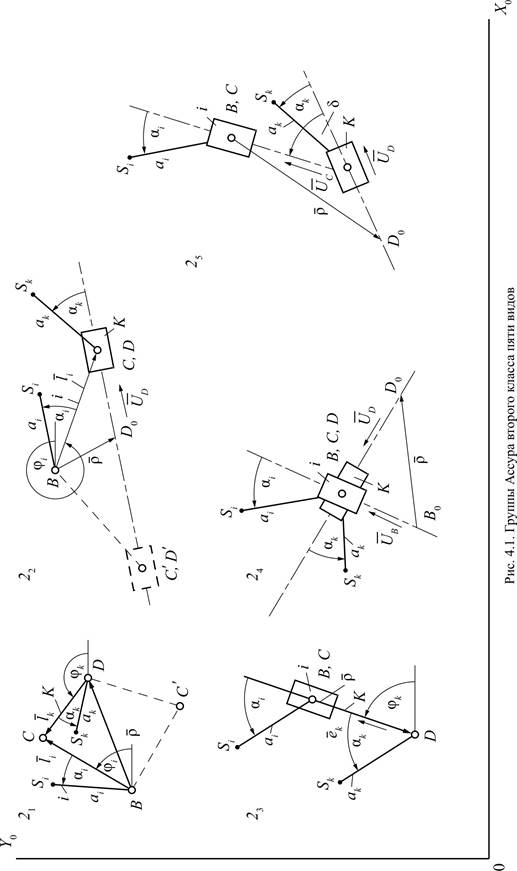
Максимальное число элементов входов зафиксировано в группе четвертого вида, т.к. она включает в себя две внешние поступательные пары (см. рис. 3.1). При решении задач о скоростях и ускорениях должны быть известны первые и вторые производные от входов, используемые в задаче о положениях. Обозначая буквой и первые производные, а цифрой 2 вторые, составим еще две таблицы входов. Такое обозначение производных наиболее удобно при написании программ для вычисления машин.
Входы, приведенные в табл. 3.1, 3.2, 3.3, изменяются при движении механизма, поэтому назовем их переменными признаками групп. Кроме переменных признаков необходимо задавать постоянные признаки, к которым относятся длины звеньев, отрезки и углы, характеризующие положения центров масс звеньев. В соответствии с рис. 3.1сведем постоянные признаки групп в таблицу.
Таблица 3.1
Входы в группы при решении задачи о положениях
| Группа | ||||||||
| 21 | 
| 
| – | – | 
| 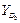
| – | – |
| 22 | 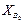
| 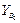
| – | – | 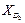
| 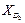
| 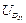
| 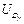
|
| 23 | 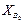
| 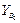
| – | – | 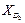
| 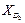
| – | – |
| 24 | 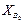
| 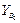
| 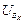
| 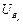
| 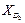
| 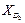
| 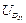
| 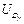
|
| 25 | 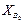
| 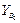
| – | – | 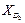
| 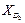
| 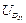
| 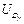
|
Таблица 3.2
Входы в группы при решении задачи о скоростях
| Группа | ||||||||
| 21 | 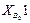
| 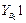
| – | – | 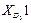
| 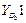
| – | – |
| 22 | 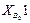
| 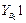
| – | – | 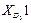
| 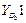
| 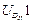
| 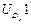
|
| 23 | 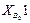
| 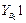
| – | – | 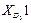
| 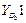
| – | – |
| 24 | 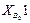
| 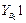
| 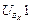
| 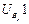
| 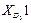
| 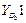
| 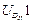
| 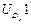
|
| 25 | 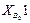
| 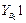
| – | – | 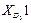
| 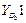
| 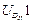
| 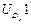
|
Таблица 3.3
Входы в группы при решении задачи об ускорениях
| Группа | ||||||||
| 21 | 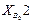
| 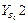
| – | – | 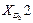
| 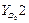
| – | – |
| 22 | 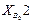
| 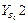
| – | – | 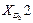
| 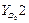
| 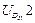
| 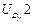
|
| 23 | 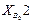
| 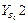
| – | – | 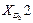
| 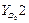
| – | – |
| 24 | 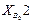
| 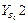
| 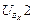
| 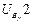
| 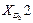
| 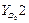
| 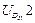
| 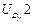
|
| 25 | 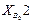
| 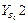
| – | – | 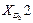
| 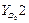
| 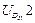
| 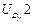
|
В этой таблице только первый столбец требует пояснений. При рассмотрении кинематики групп Ассура будет внесено определение величины δ – коэффициент, который учитывает сборку группы.
Таблица 3.4
Постоянные признаки групп
| Группа | |||||||
| 21 | δ | lk | li | ai | ak | αi | αk |
| 22 | δ | – | li | ai | ak | αi | αk |
| 23 | – | – | – | ai | ak | αi | αk |
| 24 | – | – | – | ai | ak | αi | αk |
| 25 | δ | – | – | ai | ak | αi | αk |
Дата добавления: 2020-07-18; просмотров: 625;











