Несколько узлов с заданным напряжением
В реальных электроэнергетических системах число узлов, где задано напряжение, может быть значительно больше одного (узлы n+1,…, n+k). Читателю предлагается самостоятельно доказать, что в этом случае системы уравнений (2.3),(2.4) преобразуются к виду
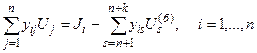 , ,
| (2.7) |
или в матричном виде
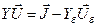 . .
| (2.8) |
Пример. Записать матрицы УУН для сети, представленной на рис. 2.5.


Рис. 2.5. Пример электрической сети с двумя базисными напряжениями
Расчетные матрицы:
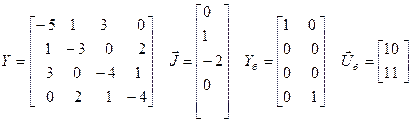 .
.
В матричном виде УУН имеют вид
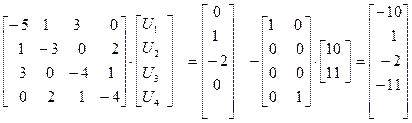
Решение рассматриваемой системы УУН: 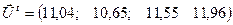
Формы записи УУН для сети переменного тока
Линейные УУН
В УУН сети постоянного тока заданы токи в узлах, а неизвестные напряжения входят в уравнения первой степенью. Специфика УУН для однофазной сети переменного тока заключается в том, что здесь учитываются комплексные величины токов, напряжений и проводимостей, но по форме уравнения идентичны
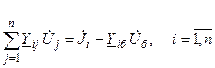 . .
| (2.9) |
Как правило, в практике имеют дело с 3-х фазнымиэлектрическими сетями, линейными напряжениями и фазными токами. Для использования УУН в виде (2.9) линейные напряжения приводятся к фазным 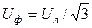 . Тогда УУН имеют вид
. Тогда УУН имеют вид
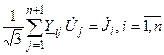 ,
,
или
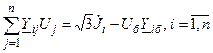 . .
| (2.10) |
По аналогии с линейными напряжениями, которые в 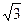 больше фазных, вводят понятие линейных токов, которые также в
больше фазных, вводят понятие линейных токов, которые также в 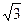 больше фазных. В этом случае система (2.10) преобразуется к виду (2.9), с учетом того, что если система однофазная, то в правой части токи - фазные, а если рассматривается трехфазная система, где определяются линейные напряжения, то в правой части записываются линейные токи.
больше фазных. В этом случае система (2.10) преобразуется к виду (2.9), с учетом того, что если система однофазная, то в правой части токи - фазные, а если рассматривается трехфазная система, где определяются линейные напряжения, то в правой части записываются линейные токи.
Программная реализация решения системы линейных комплексных уравнений имеет громоздкую структуру с определением операций с комплексными числами. Более быстрые алгоритмы получаются при преобразовании комплексной системы уравнений в действительную. В зависимости от представления комплексных чисел возможны два подхода - УУН для сети переменного тока в прямоугольной (декартовой) системе координат и в полярных координатах.
В прямоугольной системе координат комплексные величины 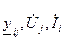 представляются в виде
представляются в виде
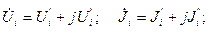
| (2.11) |
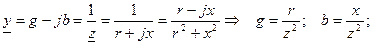
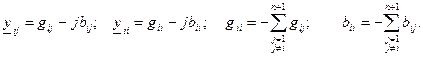
| (2.12) |
Выполнив подстановку (2.11), (2.12) в (2.10) получаем
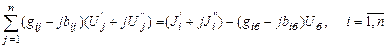 ,
,
т.к. для базисного напряжения обычно принимается 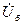 =Uб + j0.
=Uб + j0.
Два комплексных числа равны, если равны их действительные и мнимые составляющие. Отсюда система уравнений (2.10) преобразуется к виду
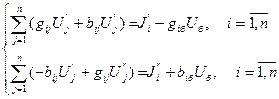
| (2.13) |
В матричной форме данная система уравнений может быть представлена в виде, рекомендуемом для запоминания
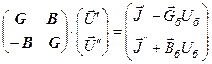
| (2.14) |
Пример. Составить УУН для сети переменного тока, представленной на рис. 2.6 .
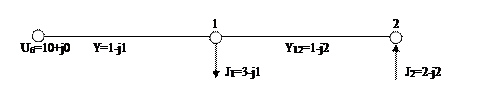

Рис. 2.6. Сеть переменного тока
Решение. Напомним, что проводимости представляются в виде (2.12)). Отсюда матрицы проводимостей
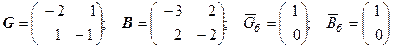 .
.
УУН в матричной форме
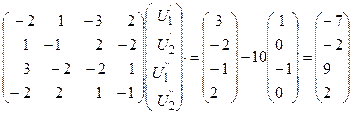 .
.
УУН в канонической форме
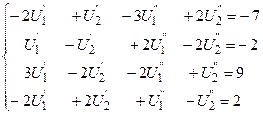
Дата добавления: 2020-07-18; просмотров: 641;











