Регулирование скорости вращения асинхронного двигателя изменением частоты питающего напряжения

Данный способ, называемый иногда частотным, широко исполь­зуется для качественного регулирования в первую очередь скорос­ти АД и широко применяется в настоящее время. Принцип его зак­лючается том, что изменяя частоту f₁ питающего АД напряжения, можно в соответствии с выражением для скорости вращения электромагнитного поля, созданного обмоткой статора,

ω₁=2πf₁/р_п изменять его ско­рость Ω, получая различные искусственные характеристики. Этот способ обеспечивает плавное регулирование скорости в широком диапазоне, а получаемые при этом характеристики обладают высо­кой жесткостью. Частотный способ к тому же отличается и еще од­ним весьма важным свойством: регулирование скорости АД в этом случае не сопровождается увеличением его скольжения, поэтому по­тери мощности, определяемые по (178), оказываются небольшими.

Для лучшего использования и получения высоких энергетичес­ких показателей работы АД (коэффициентов мощности, полезного действия и перегрузочной способности) одновременно с частотой необходимо изменять и подводимое к нему напряжение.

Введём обозначения относительных параметров АД

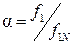- относительное значение частоты питающего напряжения;

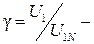относительное значение величины напряжения, подаваемого на обмотку статора;

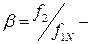абсолютное скольжение АД;

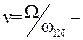относительное значение скорости вращения вала АД;

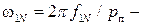угловая частота вращения электромагнитного поля АД при номинальном значении частоты питающего напряжения f_1N;

р_п - число пар полюсов АД;

ν=α- β;

β=αs;

s=(ω₁-Ω)/ω₁– относительное скольжение АД;

μ=М/М_N – относительное значение момента.

В 1925 году академиком Костенко М.П. был сформулирован основной закон частотного управления АД.

Для того чтобы асинхронный двигатель на всем диапазоне регулирования скорости вращения работал бы с постоянным и равным номинальному значению коэффициента полезного действия КПД, с постоянным и равным номинальному значению коэффициента мощности cosφ_N и c постоянным и равным номинальному значению абсолютного скольжения β напряжение, подаваемое на обмотку статора, необходимо регулировать пропорционально его частоте и корню квадратному из момента:

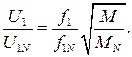(223)

Или в относительных параметрах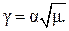

Отметим, что этот закон сформулирован для идеализированного АД, в котором помимо пренебрежения насыщением магнитной цепи принято равным нулю активное сопротивление обмотки статора (r₁=0). Приняты также синусоидальная форма напряжения, питающего двигатель, и наличие принудительной системы охлаждения двигателя.

Практическая реализация основного закона частотного управления требует, как это видно из (223) измерения текущего значения момента, что существенно усложняет систему регулирования частотно – управляемого привода.

В зависимости от характера нагрузки на валу АД различают три частных случая закона М.П. Костенко для регулирования по граничному моменту.

При постоянном моменте нагрузки М_с = const напряжение на статоре должно регулироваться пропорцио­нально его частоте

U₁/f₁ = const. (224)

Для вентиляторного характера момента нагрузки соотношение (223) будет иметь вид

U₁/(f₁²) = const. (225)

При нагрузке с постоянной мощностью

U₁/√f₁= const. (226)

Таким образом, при реализации частотного способа регулиро­вания скорости АД используется преобразователь частоты, кото­рый позволяет также регулировать и напряжение на его статоре.

Отметим, что на практике используются и более сложные по срав­нению с выражениями (224)... (226) законы частотного управления, в частности учитывающие наличие активного сопротивления.

Из изложенного выше следует, что для реализации частотного управления АД необходим преобразова­тель частоты и напряжения 1 (в дальнейшем используется обозна­чение ПЧ), на вход которого подается стандартное напряжение сети U₁ (220, 380 В и т.д.) промышленной частоты f₁ = 50 Гц, а с выхода снимается переменное напряжение U_{1 рег} регулируемой частоты f_1рег (см. рис. 81, а). Соотношения U_{1 рег} и f_1рег определяются формулами (224)... (226). Регулирование выходной частоты и напряжения осу­ществляется с помощью управляющего сигнала U_у, который задает требуемое значение скорости двигателя 2.

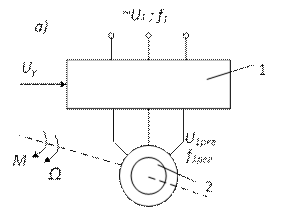
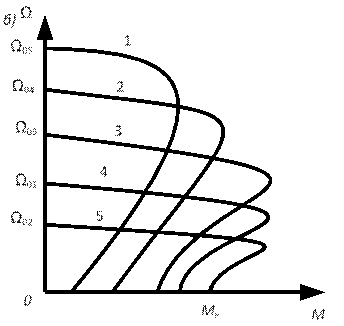
Рис. 81. Схема включения АД (а) и его механические характеристики при изменении часто­ты (б)

Анализ механических характеристик двигателя при его управ­лении по наиболее распространенному закону U₁/f₁ = const показы­вает, что скорость идеального холостого хода двигателя Ω₀=ω₁ изменяет­ся пропорционально частоте напряжения, а критический момент М_к остается неизменным, что следует из упрощенного выражения (184). Действительно, так как ω₁~ f₁ и х_к ~f₁, то критический мо­мент М_к ~ U₁²/ f₁² ~ U₁/f₁ = const.

Механические характеристики (см. рис. 81, б) при частотном регулировании разделяются на характеристики, соответствующие частотам ниже номинальной (сетевой) f_1ном и выше ее.

Область частот f₁<f_1ном. В этой области для частот f_1,3 = f_1ном; f_1,4 <f_1,3; f_1,5 <f_1,4; (характеристики 3,...,5) выполняется соотношение U₁/f_x = const, так как напряжение, подводимое к АД, регулируется от номинального (сетево­го) в сторону уменьшения. Поэтому М_к = const и АД имеет постоянную перегрузочную способность. Отметим, что из-за влияния сопротивле­ния r₁, которое не учитывалось при выводе формулы (156), момент М_к в области малых скоростей АД несколько снижается, поэтому для под­держания М_к=const напряжение при малой частоте должно уменьшаться не пропорционально ей, а несколько в меньшей степени.

Область частот f₁ >f_1ном. По условиям нормальной работы АД нельзя повышать напряжение сверх номинального (паспортного). Поэтому регулирование скорости в этой области ведется при U₁ =U_1N=const (характеристики 1 и 2 при частотах f_{1, 1} и f_{1, 2}), т.е. кри­тический момент М_к в соответствии с (156) будет уменьшаться при увеличении частоты f₁ (f_{1, 1} >f_{1, 2} >f_1ном).

В настоящее время большое распространение получили полупроводниковые преобразователи частоты. Использование ПЧ позволило существенно улучшить технико-экономические показатели асинхронного ЭП­ и расширить их область применения. Преобразователи частоты для асинхронного ЭП рассмотрены в разд. 7.

Частотное управление при U₁/f₁= const [9]

Если в выражении для основного закона частотного управления принять момент постоянным и равным номинальному, т.е. М=М_N, то получим частный случай основного закона частотного управления, который обычно называют «номинальным» законом:

U₁/ U_1N= f₁/ f_1Nили U₁/f₁ = const

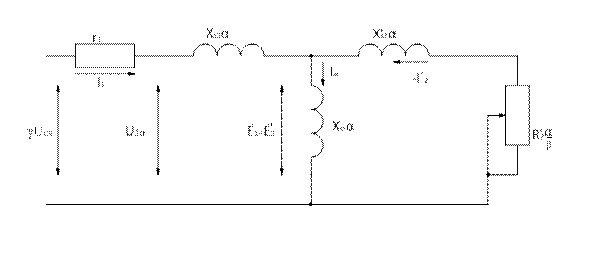
Рис.82.Схема замещения АД при частотном способе регулирования скорости вращения

Такое название закона объясняется тем, что ряд серий асинхронных короткозамкнутых двигателей имеют табличные заводские данные, указанные применительно к закону U₁/f₁ = const [15]. Структурная схема системы частотного управления, реализующая «номинальный» закон, приведена на рис. 82, где ЗИ – задатчик интенсивности; ФП – функциональный преобразователь; ПЧ – преобразователь частоты; РЧ – регулятор частоты; РН – регулятор напряжения; АД – асинхронный двигатель; К_ос – усилитель канала обратной связи; α – сигнал управления частотой; γ – сигнал управления напряжением.

Посредством ЗИ задается интенсивность (темп) изменения управляющего сигнала во времени. Этот сигнал по одному каналу поступает в РЧ, а по второму – через ФП в РН. Возможно введение обратной связи по напряжению в канале РН в целях компенсации колебаний напряжения сети и падения напряжения в РЧ. Однако, по сути эта система является разомкнутой системой частотного управления. Диапазон регулирования скорости вращения не превышает (2…5):1 вниз от номинальной. В диапазоне 2:1 двигатель работает в условиях, близких к номинальным. Дальнейшее увеличение диапазона регулирования приводит к уменьшению потока, обусловленного падением напряжения в активных сопротивлениях обмотки статора. Поскольку при снижении частоты питания пропорционально ей уменьшаются только реактивные сопротивления, а активные сопротивления остаются неизменными, то при низких частотах падение напряжения на активном сопротивлении статора увеличивается.

Действительно, напряжение, приложенное к обмотке статора 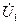, уравновешивается ЭДС 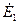, индуктируемой в этой обмотке основным магнитным потоком Ф и падением напряжения на сопротивлениях обмотки статора ( ):

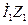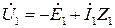
Так как 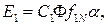то, 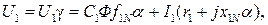откуда получаем

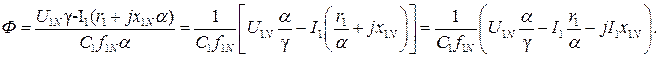
(227)

Из (227) видно, что при «номинальном» законе частотного управления (α = γ) уменьшение частоты f₁ (α<1) приводит к увеличению падения напряжения на активном сопротивлении обмотки статора, к уменьшению потока Ф и, как это следует из (174), к уменьшению электромагнитного момента М.

В результате этого понижается жесткость механических характеристик, увеличиваются потери двигателя, снижается надежность его работы из-за уменьшения перегрузочной способности, а при частотах, близких к нулю, работа двигателя оказывается вообще невозможной.

На рис. 84 представлена зависимость момента двигателя М/М_Nот относительной частоты тока ротора 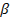для различных значений f₁, рассчитанная по выражению момента, записанному в модифицированной форме формулы Клосса.

Из рис. 84 видно, насколько резко уменьшается момент АД (Р_N=1,5 кВт) при снижении частоты напряжения статора. В генераторном режиме мощность и падение напряжения в статоре изменяют свои знаки, вследствие чего увеличивается ЭДС Е₁ и поток в воздушном зазоре. Следовательно, момент в генераторном режиме возрастает при уменьшении частоты f₁, особенно в диапазоне низких частот f₁. Если ток статора не ограничивается, то момент, развиваемый асинхронной машиной в генераторном режиме, который, как известно, носит тормозной характер, по условиям механической прочности может оказаться чрезмерным и вывести машину из строя.

При наличии насыщения магнитной цепи происходит некоторое уменьшение момента в генераторном режиме по сравнению с его расчетным значением, приведенным на рис. 84.

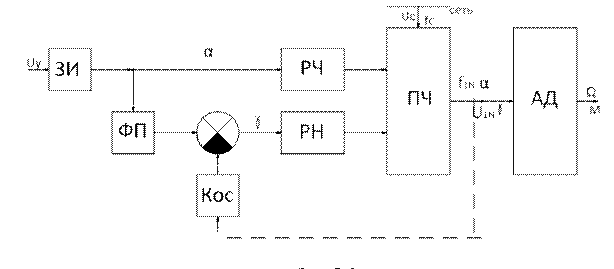
Рис.83.Структурная схема частотного управления АД при U₁/f₁=const

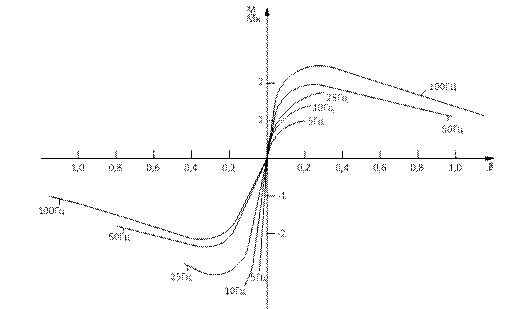
Рис.84.Механические характеристики АД при частотном управлении по закону U₁/f₁=const

Частотное управление с компенсацией падения напряжения на активном сопротивлении обмотки статора [9]

Влияние активного сопротивления обмотки статора на характеристики асинхронного двигателя может быть существенно ослаблено путем непрерывной компенсации падения напряжения на активном сопротивлении статора, исключающей влияние этого сопротивления на поток двигателя. Впервые эта задача была решена А.А. Булгаковым, который предложил регулировать пропорционально частоте не напряжение, приложенное к обмотке статора, а так называемое «внутреннее» напряжение схемы замещения, т.е. напряжение за активным сопротивлением 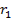схемы замещения (см. рис. 82):

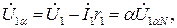(228)

где U_1αN= U_1αпри U₁= U_1Nи I₁=I_1N.

Нетрудно показать, что при регулировании с компенсацией напряжения на активном сопротивлении обмотки статора (с Ir - компенсацией) полный поток двигателя 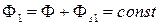, где Ф – основной (рабочий) поток (поток в воздушном зазоре); Ф_s1 - поток рассеяния обмотки статора.

Из уравнения равновесия напряжений, составленного для статорной цепи двигателя, можно получить

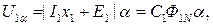
где индекс «N» относится к параметрам при номинальной частоте.

Из-за постоянства потока Ф₁ при регулировании с Ir - компенсацией этот закон принято называть законом постоянного полного потока.

Рассмотрим структурную схему (рис. 85), реализующую указанный закон. Сравнивая структурные схемы, представленные на рис. 83 и рис. 85, можно отметить следующее. В схему, изображенную на рис. 85, введено вычислительное устройство (ВУ), на вход которого подаются сигналы, пропорциональные U₁, I₁, f₁,а с выхода его снимается сигнал, пропорциональный контролируемой величине U_1α. Сигнал U_1α сравнивается с эталонным сигналом U_эт, вырабатываемым ЗИ, и их разность δU подается на вход РН.

Функциональный преобразователь (ФП) введен в канал регулирования частоты и реализует функцию U_эт/ f₁=const.

ВУ может быть выполнено в виде счетно-решающего аналогового устройства или физической модели двигателя. В последнем случае ВУ представляет собой последовательное соединение активного сопротивления и дросселя, подмагничиваемого током двигателя. Схема получается простой, но не свободной от существенных недостатков, вызванных различными температурными режимами работы двигателя и модели. При работе двигателя обмотки его нагреваются, величина их активных сопротивлений увеличивается, в то время как активное сопротивление физической модели практически не меняется. Отклонение параметров физической модели от параметров двигателя приводит к появлению ошибок в сигнале δU и нарушению условий выполнения закона постоянного полного потока. Для устранения этого недостатка необходимо ввести в ВУ сигнал, пропорциональный температуре обмотки статора t (на рис. 85 показан пунктиром). С этой целью в пазах статора размещают термодатчики и соединяют их с ВУ. При этом оказывается, что величина активного сопротивления физической модели зависит от температурного режима обмотки статора. Погрешность сигнала δU существенно уменьшается. Закон частотного управления с Ir -компенсацией имеет достаточно простое выражение

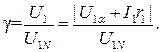(229)

Как показано в [9], при регулировании с Ir - компенсацией момент M и параметр абсолютного скольжения β не зависят от частоты .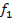

На рис. 88 приведены зависимости M/M_N=f(β)для частотного управления с Ir -компенсацией (кривая 1) и «номинального» закона (кривые 2, 3, 4), откуда нетрудно установить достоинства частотного управления с Ir -компенсацией – во всем диапазоне изменения частоты f₁условия работы асинхронного двигателя остаются такими же, как и при номинальной частоте f_1N.

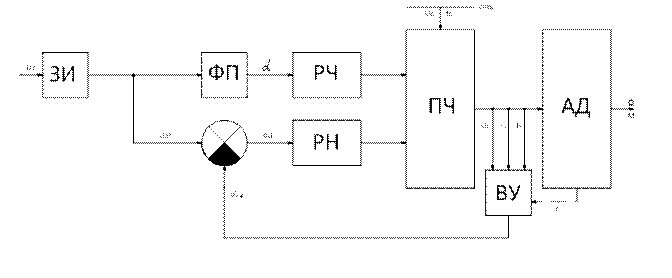
Рис.85.Структурная схема частотного управления АД с компенсацией падения напряжения на активном сопротивлении обмотки статора

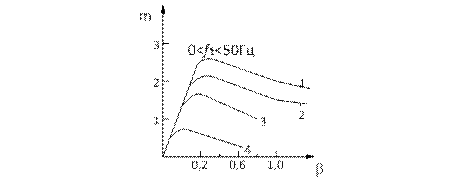
Рис.88. Механические характеристики АД при частотном управлении с компенсацией падения напряжения на активном сопротивлении обмотки статора (1) и по закону U₁/f₁=const (2,3,4)

Частотное управление с компенсацией падения напряжения на полном сопротивлении обмотки статора [9]

Частотное управление с Ir -компенсацией имеет и очевидный недостаток: с увеличением момента нагрузки рабочий поток двигателя, т.е. поток в его воздушном зазоре, будет уменьшаться. Действительно, с увеличением момента нагрузки возрастает ток статора I₁и повышается падение напряжения на индуктивном сопротивлении рассеяния обмотки статора ΔU_x1=jI₁x₁. Это обстоятельство является причиной уменьшения тока намагничивания I_μ, а, следовательно, и потока в воздушном зазоре, т.е. рабочего потока.

Режим работы асинхронного двигателя при частотном управлении с постоянным рабочим потоком впервые был рассмотрен А.А. Булгаковым [9]. Им было предложено регулировать напряжение, подаваемое на обмотки статора, в функции частоты и нагрузки путем повышения напряжения на величину, необходимую для полной компенсации падения напряжения на полном сопротивлении обмотки статора при протекании по ней тока I₁. Таким образом, в функции частоты регулируется напряжение ветви контура намагничивания E_1α, которое определяется как

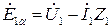
откуда видно, что для реализации частотного управления с постоянным рабочим потоком необходимо регулировать напряжение U₁ при изменении частоты f₁таким образом, чтобы выполнялось условие E_1α/f₁=const.При регулировании напряжения за базовый поток может быть принят поток при номинальном моменте нагрузки

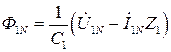
Закон частотного управления с постоянным рабочим потоком можно выразить следующим образом:

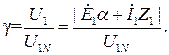(230)

Структурная схема, реализующая закон постоянного рабочего магнитного потока, представлена на рис. 89. Рабочий поток измеряется с помощью датчиков ЭДС Холла, размещенных определенным образом в воздушном зазоре двигателя. Датчики ЭДС Холла измеряют мгновенное значение потока, а для работы системы необходим сигнал, пропорциональный действующему значению потока. Это преобразование осуществляет усилитель - формирователь в цепи обратной связи К_ф.

Также как и в предыдущей схеме при частотном управлении с компенсацией падения напряжения на полном сопротивлении обмотки статора момент и критическое скольжение не зависят от частоты f₁ [9].

На рис. 90 приведены две зависимости М/М_N=f(β). Кривая 1 соответствует частотному управлению при постоянном рабочем магнитным потоком, а кривая 2 представляет собой механическую характеристику этого же двигателя при

номинальных значениях напряжения и частоты. Отсюда нетрудно установить, что при регулировании частоты по закону постоянного рабочего потока двигатель развивает значительно больший момент. Так, опрокидывающий момент М_maxпри регулировании с постоянным рабочим магнитным потоком может в 2-3 раза превышать М_max при регулировании с постоянным полным магнитным потоком. При этом и напряжение U₁оказывается значительно выше, чем при регулировании с Ir - компенсацией.

На рис. 91 приведены кривые зависимости γ=f(β) при изменении 0<α<1, откуда видно, что в области относительно высоких значений f₁≈ (0,6,…,1,0)f_1Nнаблюдается существенное превышение напряжения статора над номинальным значением U_1N, особенно при больших значениях скольжения в пусковых режимах. Это ограничивает применение закона регулирования постоянным рабочим потоком в указанных областях изменения f₁ и β.

Рассмотренные выше системы регулирования реализуют управление по граничному моменту М_с=М_N=const, т.е. не предусматривают длительного регулирования напряжения пропорционально .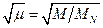

Введение в систему регулирования обратной связи по текущему значению момента двигателя позволяет снижать величину потока двигателя при уменьшении момента нагрузки. Тем самым улучшаются энергетические показатели двигателя при малых нагрузках и сохраняется его перегрузочная способность. В канал обратной связи по моменту при μ>1необходимо ввести ограничение сигнала, чтобы избежать насыщения магнитной цепи двигателя. Введение обратной связи по моменту не устраняет зависимости потока от частоты f₁и падения напряжения на сопротивлениях обмотки статора.

На рис. 92 приведена структурная схема системы регулирования с компенсацией падения напряжения на сопротивлениях обмотки статора и с дополнительным регулированием напряжения в функции текущего момента. С двигателя снимают сигнал, пропорциональный электромагнитному моменту М_эм, и подают его на функциональный преобразователь (ФП). С выхода ФП снимают сигнал, пропорциональный 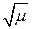, и через усилитель-ограничитель (УО) подают на один из входов блока умножения П. На другой вход блока П подают сигнал, пропорциональный произведению 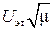, и подают его в канал регулятора напряжения. Как указывалось выше, сигнал, пропорциональный 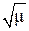, не должен превышать того значения, которое он имеет при М=М_N. Ограничение этого сигнала по амплитуде осуществляет УО.

Получить сигнал, пропорциональный М_эм, весьма сложно. На практике обычно применяют сигнал, пропорциональный активной составляющей тока статора I_1α=I₁cosφ, поскольку М_эм двигателя ей пропорционален.

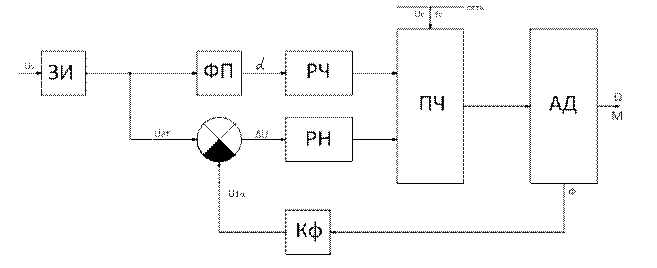Рис.89. Структурная схема частотного управления АД с компенсацией падения напряжения на полном сопротивлении обмотки статора

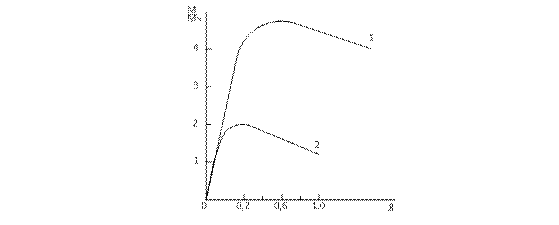
Рис.90.Механическая характеристика АД при частотном управлении с компенсацией падения напряжения на полном сопротивлении обмотки статора (1) и механическая характеристика двигателя (2) при номинальных значениях напряжения и частоты

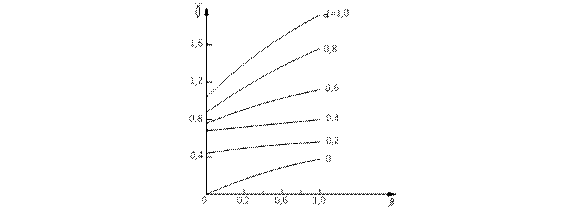
Рис.91.Зависимость напряжения, подаваемого на обмотку статора, от абсолютного скольжения на диапазоне регулирования частоты 0<α <1,0

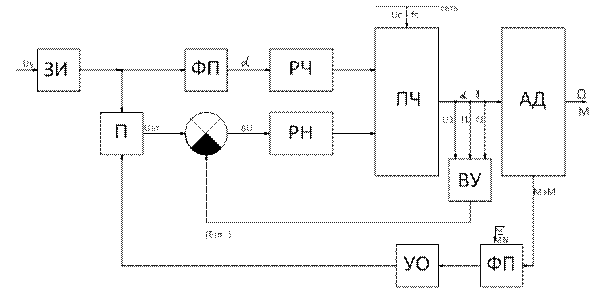
Рис.92. Структурная схема частотного управления АД с компенсацией падения напряжения на сопротивлениях обмотки статора и с дополнительным регулированием напряжения в функции текущего момента

Частотное управление с обратной связью по абсолютному скольжению[9]

Дополнительное регулирование напряжения, пропорциональное 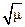, возможно без непосредственного измерения электромагнитного момента или активной составляющей тока статора. Вспомним еще раз формулировку основного закона частотного управления, данную М.П. Костенко, и обратим внимание на то, что абсолютное скольжение остается постоянным при регулировании напряжения 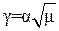. Отсюда можно сделать вывод, что если при частотном управлении регулировать напряжение таким образом, чтобы абсолютное скольжение оставалось неизменным, то работа двигателя по своим параметрам будет близка к работе двигателя при управлении по основному закону. Измерить абсолютное скольжение технически проще, чем электромагнитный момент.

Связь между моментом двигателя от потока и тока обмотки ротора 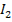установлена соотношением (174)

М=С_мФ I₂cosψ₂

В соответствии со схемой замещения ток обмотки ротора

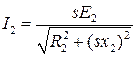
При частотном управлении скольжение s обычно невелико, поэтому sx₂<<R₂, и тогда

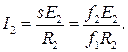
Так как поток Ф пропорционален отношению E₂/f₁, то

I₂=k₁Фf₂

т.е. ток ротора прямо пропорционален частоте тока ротора f₂. Момент

M=k_м Ф²f₂, (231)

где k₁ и k_м – постоянные коэффициенты тока ротора и момента соответственно.

Анализируя (231), видим, что при постоянном рабочем потоке и малых скольжениях момент двигателя прямо пропорционален абсолютному скольжению.

Таким образом, введение в систему регулирования дополнительного контура поддержания заданной величины абсолютного скольжения, воздействующего на напряжение двигателя, автоматически обеспечивает регулирование напряжения пропорционально 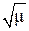. Структурная схема системы регулирования с обратной связью по абсолютному скольжению приведена на рис. 93.

Сигнал, пропорциональный абсолютному скольжению β, поступает на ограничитель (Ог). Ограничение сигнала необходимо при моментах нагрузки М>М_max. После Ог сигнал поступает на узел сравнения, где он сравнивается с эталонным сигналом U_{эт β}. Сигнал, равный разности двух сравниваемых сигналов, поступает на вход усилителя (У). Усиленный сигнал поступает на вход сумматора ∑, где он суммируется с сигналом управления, в результате чего происходит автоматическое изменение напряжения U_эт.

Эта система регулирования отличается простотой, и ее реализация не вызывает особых трудностей.

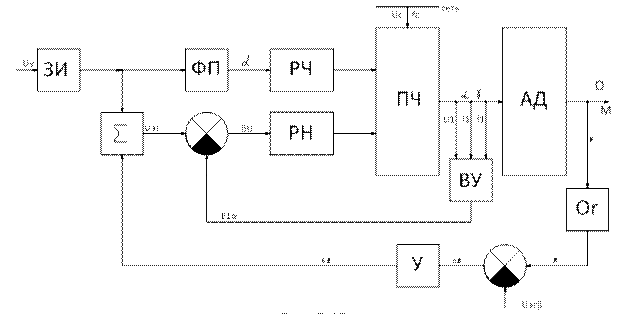
Рис.93. Структурная схема частотного управления АД собратной связью по абсолютному скольжению

Частотно-токовое управление [9]

Рассмотренные выше системы регулирования реализуют так называемое частотное управление, основанное на управлении величиной напряжения, подаваемого на асинхронный двигатель. Преобразователь частоты (ПЧ) является в этом случае источником напряжения. Частотному управлению свойственны определенные недостатки:

- низкое качество регулирования скорости двигателя;

- сложность реализации частных законов частотного управления, для которых рабочий поток требуется регулировать в функции момента двигателя.

От этих недостатков практически свободны системы регулирования, реализующие так называемый частотно-токовый способ управления, при котором управляют величиной тока статора двигателя. Суть способа состоит в следующем. Если поддерживать постоянными рабочий поток и частоту тока ротора, то и ток обмотки ротора будет постоянным. При постоянном потоке ток намагничивания I_μ также постоянен. Следовательно, и ток обмотки статора 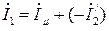будет постоянным.

Отсюда можно сделать важный вывод: если в системе регулирования поддерживаются постоянными частота тока ротора (или абсолютное скольжение) и рабочий поток, то во всем диапазоне регулирования скорости вращения двигателя ток статора и момент будут постоянными. Если же регулировать ток статора и частоту ротора, то можно косвенно регулировать рабочий поток двигателя, а, следовательно, и момент двигателя. Способ управления, при котором осуществляют регулирование тока обмотки статора в соответствии с входным управляющим сигналом, пропорциональным требуемому моменту, и сигналом, пропорциональным угловому положению ротора, называется частотно-токовым.

Структурная схема системы регулирования, в которой реализован частотно-токовый принцип управления, приведена на рис. 93.

Сигнал регулятора тока (РТ) формируется функциональным преобразователем (ФП), на вход которого подается сигнал, пропорциональный заданному значению абсолютного скольжения, который вырабатывает блок регулятора скорости (РС). На вход РС поступает разностный сигнал от задатчика интенсивности (ЗИ) и сигнала обратной связи, пропорционального величине абсолютного скольжения. Контроль за величиной тока обмотки статора двигателя осуществляется датчиком тока (ДТ). Этот сигнал сравнивается с выходным сигналом ФП. Полученный в результате этого сравнения разностный сигнал и является сигналом управления РТ. Сигнал для регулятора частоты (РЧ) получают суммированием двух сигналов – от РС и датчика абсолютного скольжения.

Преобразователь частоты в этом случае является источником переменного тока. При частотно-токовом управлении асинхронным двигателем величина и частота тока обмотки ротора значительно меньше, чем при прямом пуске двигателя. Это обстоятельство можно использовать при проектировании асинхронных двигателей специально для частотно-токового управления, если уменьшить сопротивление обмотки ротора, как индуктивное, так и активное.

При частотно-токовом способе управления возможно скачкообразное изменение момента нагрузки. При этом асинхронный двигатель не будет опрокидываться, так как в этих режимах всегда формируется максимальный сигнал регулятора тока, соответствующий электромагнитному моменту требуемой величины.

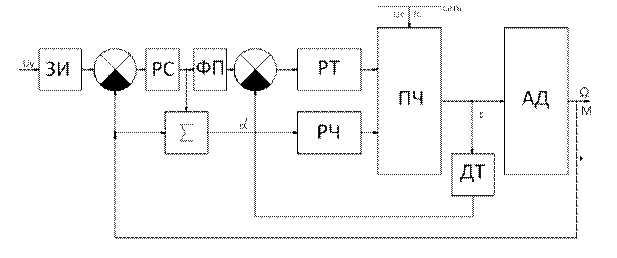
Рис.93.Структурная схема частотно – токового управления АД

Векторное управление асинхронными двигателями [9]

Название данного методе регулирования частоты вращения асинхронного двигателя (АД) не является устоявшимся. Кроме векторного управления АД встречаются и другие названия: подчиненно-векторное управление, ориентация по электромагнитному полю в зазоре, transvektor (преобразователь векторов).

Принцип рассматриваемого метода регулирования заключается в том, что управляющие воздействия – амплитуда и частота напряжения, приложенного к обмотке статора, регулируются таким образом, что обеспечивается такое же, как и в двигателях постоянного тока, угловое соотношение между результирующим током статора и потокосцеплением ротора. При этом регулировочные и механические характеристики АД подобны соответствующим характеристикам электроприводов на базе машин постоянного тока.

Момент, развиваемый двигателем постоянного тока с независимым возбуждением, зависит от потока в воздушном зазоре и тока якоря:

M_дпт=С_мФI, (232)

где C_м - конструктивный коэффициент двигателя постоянного тока.

При работе двигателя постоянного тока на естественной характеристике поток мало меняется с изменением момента нагрузки (реакцией якоря пренебрегаем). С увеличением момента нагрузки частота вращения машины постоянного тока снижается, вызывая соответствующее уменьшение ЭДС, индуктируемой в якоре, что вызывает повышение момента двигателя до величины, достаточной для уравновешивания нового момента нагрузки. Это свойство саморегулирования электрических машин постоянного тока аналогично свойству автоматических регуляторов со статической характеристикой.

Момент, развиваемый асинхронным двигателем, можно определить с помощью различных электромагнитных параметров, отражающих взаимосвязь электромагнитных полей статора и ротора АД. Поэтому выберем форму записи электромагнитного момента АД, эквивалентную по смыслу моменту двигателя постоянного тока:

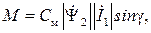(233)

где ψ₂ - вектор потокосцепления ротора; I₁ - вектор результирующего тока статора; C_м - конструктивный коэффициент электродвигателя; γ - угол сдвига между указанными векторами. Взаимное положение векторов ψ₂ и I₁ показано на рис.94.

Выражения (232) и (233) подобны по форме записи. В (231) мы пренебрегли размагничивающей реакцией якоря, поэтому векторы потока возбуждения и тока якоря взаимно перпендикулярны.

Из анализа формулы (233) можно установить следующий принцип регулирования АД. Если стабилизировать потокосцепление ротора, то электромагнитный момент АД будет пропорционален составляющей результирующего тока статора I₁, спроектированного на ось q, перпендикулярную вектору потокосцепления ротора, направление которого совпадает с осью d (см.рис. 94).

Рассмотрим подробнее векторную диаграмму, приведенную на рис.94. В системе координат α, β, жестко связанной со статором АД (ось 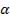направлена по оси фазной обмотки А), построены векторы результирующего тока статора I₁и потокосцепления ротора, которые вращаются в пространстве с угловой частотой поля статора ω₁. При этом скольжением пренебрегаем, что вполне допустимо при векторном управлении. Тогда частота вращения поля статора ω₁ равна частоте вращения ротора Ω.

Электромагнитные процессы в АД рассматриваются во вращающейся системе координат d, q, жестко связанной с ротором. Если ось d совместить с направлением вектора потокосцепления ротора, то величина составляющей тока обмотки статора I_q, определяющая величину электромагнитного момента, будет равна

I_1q=I₁sinγ.

Параметры ψ₂ и I_q, определяющие величину электромагнитного момента АД, непосредственно измерить невозможно, но их можно вычислить с помощью известных формул преобразования систем координат.

Измеренные фазные токи обмотки статора АД пересчитываются в токи системы координат α, β по формулам

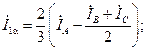
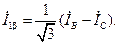
Переход от токов 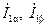к токам во вращающейся системе координат выполняется по соотношениям

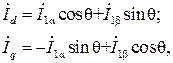
где θ - текущий угол сдвига между системами координат α, β и d, q.

Для измерения угла θ необходимо в воздушном зазоре АД разместить взаимно перпендикулярно два датчика мгновенного значения индукции, которую легко пересчитать в потокосцепление. Датчики могут быть выполнены на основе элементов Холла, магниторезисторов или специальных измерительных обмоток. При этом один датчик устанавливается по оси фазы А, а другой сдвигается на π/2 эл. рад. Информация с датчиков получается в виде синусоидальной и косинусоидальной зависимостей текущего угла поворота ротора θ . Одновременно информация с этих датчиков используется для определения модуля потокосцепления ротора.

После получения значений регулируемых параметров ψ₂ и I_q во вращающейся системе координат и сравнения их с требуемыми значениями вырабатывается управляющее воздействие во вращающейся системе координат, которое затем с помощью формул обратного преобразования от вращающейся системы координат к естественной пересчитывается в сигналы на открытие соответствующих вентилей силового полупроводникового преобразователя, питающего АД.

Реализация векторного управления АД требует достаточно сложных управляющих и функциональных устройств преобразования координат и фаз, а также осуществления компенсационных связей в случае широкого диапазона регулирования частоты вращения и момента нагрузки. Все это в определенной мере ограничивает область применения векторного способа управления АД.

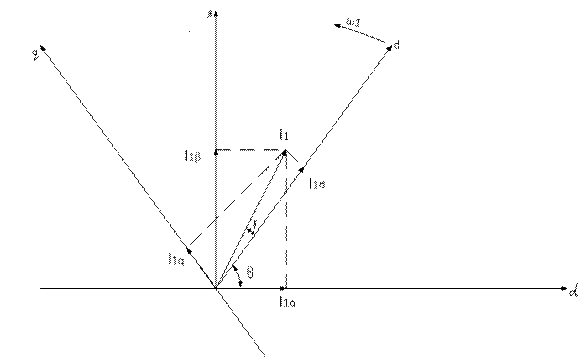
Рис.94.Векторная диаграмма токов АД