Всенаправленный измеритель малой скорости с приемником давления на двухстепенном подвесе

Измеритель малой скорости с приемником давления на двухстепенном подвесе, как и измерители ЛОРАС и КВИС, использует эффект наддува в измерительной пневматической системе полного давления. В измерителях ЛОРАС и КВИС наддув достигается за счет окружной скорости приемника давления при его вращении на штанге или на лопасти.

Измеритель малой скорости с приемником давления ПВД на двухстепенном подвесе был впервые разработан в начале семидесятых годов английской фирмой Маркони Авионикс (Marconi Avionics) и получил условное название ЛЭССИ (LASSIE) (рис. 5.21).

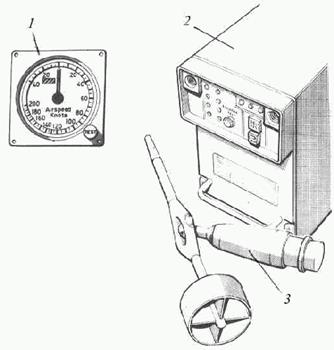
Рис. 5.21. Внешний вид измерителя ЛЭССИ: 1 – индикатор; 2 – вычислитель; 3 ‑ датчик

Измеритель ЛЭССИ состоит из индикатора 1, вычислителя 2, датчика 3. Для получения наддува в пневмосистеме Р_п датчик 3 измерителя размещается на фюзеляже вертолета под НВ. В процессе вращения НВ скорость отбрасывания потока воспринимается ПВД 1, пропорциональное ей полное давление передается по тракту 7 в вычислитель (рис. 5.22).

Как было показано во второй главе, величина наддува зависит от интенсивности вихря от НВ и составляет 50 – 130 км/ч (таблица 2.5). Это уже достаточно большие скорости, которые можно легко преобразовать в электрические сигналы для обработки их в вычислителе.

Измеритель ЛЭССИ способен воспринимать и вычислять параметры Р_п , Р_ст , Р_д , Т_т, угол атаки местный α_м , угол скольжения β_м, скорости по продольной оси ± v_х , по попереч ной оси ± v_z . Основу системы составляет ее датчик первичных аэродинамических параметров (рис. 5.22). Он представляет собой комбинированное устройство, совмещающее в себе ПВД и флюгер, закрепленные на общей штанге, свободно вращающейся на двухстепенном подвесе 2 относительно осей Х – Х и Z –Z.

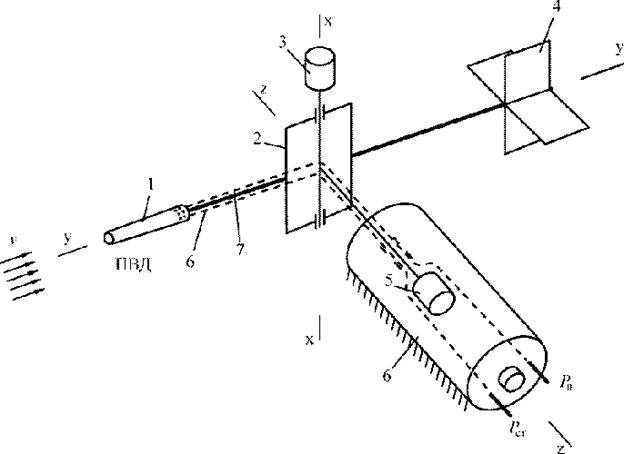
Рис. 5.22. Принципиальная схема датчика измерителя ЛЭССИ: 1 – ПВД; 2 – подвес двухстепенной; 3 – датчик угла β; 4 – флюгер; 5 – датчик угла α, 6 – корпус

ПВД и флюгер сами по себе в отдельности не являются оригинальными. Оригинальным является их сочетание вместе с подвесом. В качестве выходных устройств по угловым координатам применены БСКТ. Давления с ПВД (Р_п, Р_ст) передаются на выход устройства через подвижный шарнир с помощью гибких шлангов. Датчик устанавливается на вертолете под несущим винтом и обдувается местным воздушным потоком, который представляет собой сумму потоков от несущего винта и от скорости движения вертолета относительно воздуха. В режиме висения при отсутствии ветра ось Y – Y датчика совпадает с вертикальной осью вертолета Y – Y. Во всех остальных случаях ось Y – Y датчика совпадает по направлению с суммарным вектором воздушного потока (рис. 5.24).

На рис. 5.23 представлена векторная диаграмма воздушных потоков в месте установки датчика ЛЭССИ при полете вертолета по оси X – X без скольжения. В режиме висения весь поток НВ направлен по вектору АД. Плоскость НВ перпендикулярна вектору АД. При движении плоскость НВ наклоняется в сторону предполагаемого движения.

Появляется угол наклона плоскости НВ φ. Вектор потока АД занимает положение АС. По направлению движения вертолета появляется поток ДС – проекция вектора АС на ось X – X. Одновременно, под действием тяги винта, расположенного под углом φ, появляется вектор воздушного потока СВ. Этот вектор пропорционален воздушной скорости. В результате действия потока от НВ и от скорости полета результирующий вектор занимает положение АВ. Как показано на рисунке, датчик отслеживает положение суммарного потока АВ.

По аналогии с самолетом будем обозначать аэродинамические углы через α и β. Под углом α будем понимать аэродинамический угол между проекцией вектора суммарного потока АВ на плоскость ZOX (вектор ДВ) и вектором суммарного потока АВ. Под углом β будем понимать аэродинамический угол между вектором скорости по оси Х - Х (вектор ДВ) и проекцией вектора суммарного потока на плоскость ZOX (вектор ДВ₂ , риc. 5.24).

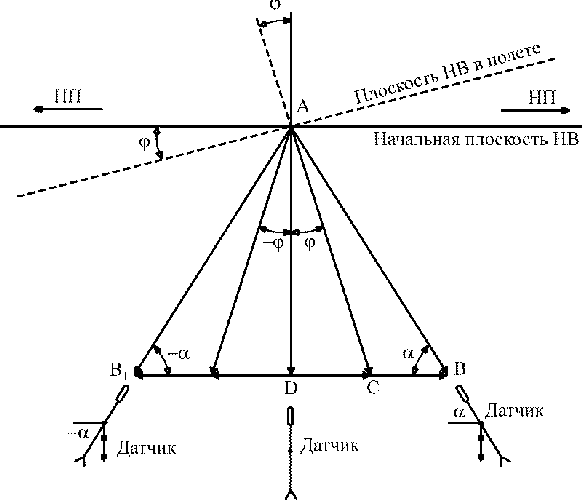
Рис. 5.23. Векторная диаграмма воздушных потоков в месте установки датчика ЛЭССИ при полете вертолета в направлении оси Х – Х без скольжения (β = 0)

Из приведенных определений следует, что полной аналогии аэродинамических углов на вертолете, определяемых с помощью всенаправленного датчика, и на самолете, нет. Тем не менее, это уже аэродинамические углы, однозначно связанные с суммарным аэродинамическим вектором, который на вертолете определяет и несущую и движущую силы. С привлечением дополнительной информации (угол автомата перекоса и др.) можно определить значения аэродинамических углов относительно фюзеляж вертолета. Эти зависимости определяются при трубных продувках и летных испытаниях конкретного вертолета.

В соответствии с векторной диаграммой рис.5.23 для полета без скольжения определим алгоритмы скорости по давлению, воспринимаемому ПВД. Напишем систему уравнений

DВ = DС + СВ

АD = АВ·sin α

DС = АD·tg φ = АВ·sin α·tg φ (5.36)

DВ = АВ·cos α

Решая совместно уравнения системы (5.36) получим:

СВ=DB–DC=AВ·cosα-AB·sinα·tgφ=AB(cos α - sin α·tg φ). (5.37)

Так как вектop СВ пропорционален величине скоростного напора по траектории полета Х - Х: СВ ≡ 0,5 ρ 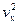, то скорость равна в околонулевом диапазоне

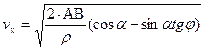. (5.38)

На рис. 5.24 представлена векторная диаграмма потоков в месте установки всенаправленного датчика аэродинамических параметров при полете вертолета со скольжением (общий случай полета).

Используя известные тригонометрические зависимости, получим систему уравнений для определения вектора СВ:

СВ = DB – DC;

DC = AD·tg φ;

AD = AB₂·sin α; (5.39)

DB = DB₂·cos β;

DB₂ = AB₂ cos α.

Решая совместно уравнения системы (5.39) получим формулу для определения скоростного напора, пропорционального скорости полета по оси Х-Х.:

СВ = DB₂·cosβ – AD · tgφ = AB₂ · cosα · cosβ - AB₂ · sinα · tgφ =

= AB₂ (cosα · cosβ – sinα · tg φ) (5.40)

Из общей формулы (5.40) получается частный случай при полете без скольжения, когда β = 0.

Для определения вектора, пропорционального скоростному напору при движении вертолета по оси Z-Z напишем систему уравнений:

C₁B₃ = DB₃ – DC₁;

DC₁ = AD · tgφ₁;

AD = AD₂·sin α; (5.41)

DB₃ = DB₂ · sinβ;

DB₂ = AB₂ · cos α.

Решая совместно уравнения системы (5.41) получим окончательную формулу для скоростного напора при полете по оси Z-Z:

C₁B₃ = DB₂ · sinβ – AD · tgφ₁ = AB₂ · cosα · sin β - AB₂ · sinα · tg φ₁ =

= AB₂(cosα · sin β - sin α · tg φ₁). (5.42)

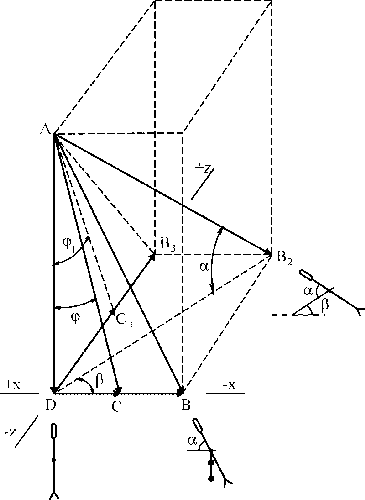
Рис. 5.24. Векторная диаграмма воздушных потоков в месте установки датчика ЛЭССИ при полете вертолета со скольжением

С учетом того, что CB = 0,5 ρ 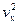, C₁B₃ = 0,5 ρ 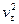, AB₂ = Р_д, получим формулы для определения скоростей по осям Х-Х и Z-Z:

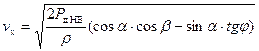, (5.43)

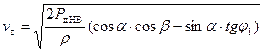, (5.44)

где P_д – динамическое давление от суммарного потока НВ вертолета и скорости полета.

Принципиальной особенностью датчика системы ЛЭССИ является наиболее благоприятные условия для измерения давлений Р_п, Р_ст. Кроме того, этот датчик способен измерять аэродинамические углы.

Недостатком датчика является ограниченная возможность по измерению малой, околонулевой скорости вертолета. Ограничение наступает из-за наличия трения в шарнире. Судя по некоторым зарубежным сведениям начальная скорость измерения составляет около 20 – 30 км/ч.

Как показали результаты теоретических исследований в облегченном варианте датчика (без обогрева) с точностью до 1^о по углам α и β можно достичь начальной скорости 15 – 20 км/ч. Кроме углов застоя датчика величина измеряемой минимальной скорости в системе аэродинамических параметров с датчиком типа ЛЭССИ определяется динамической погрешностью и порогом чувствительности по давлению (статической погрешностью) решающих устройств.

Специалисты ОАО УКБП существенно улучшили схему датчика измерителя ЛЭССИ за счет замены трубопроводов по каналам Р_п и Р_ст на специальную конструкцию воздухопроводов с магнитно-жидкостной герметизацией и за счет оптимизации флюгера с целью увеличения его момента. Эти технические решения позволили разработать датчик вертолетной скорости ДВС с улучшенными характеристиками (рис. 5.25).

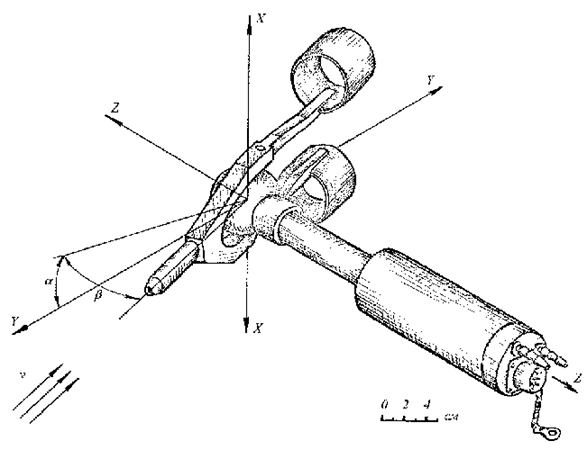
Рис. 5.25. Внешний вид датчика ДВС

В одном из вариантов ДВС были реально получены следующие технические характеристики:

- масса 1,6 кг;

- диапазон скоростей от 20 до 400 км/ч;

- диапазон по углу атаки α = ± 180°;

- диапазон по углу скольжения β = ± 70°;

- погрешность восприятия Р_д ± 0,02q;

- погрешность восприятия Р_ст ± 0,02q;

- погрешность измерения угла атаки от 0,5 до 2 градусов;

- погрешность измерения угла скольжения от 0,5 до 2 градусов.

Оригинальность рассмотренных измерителей малых скоростей сказывается на месте их установки на вертолете (рис. 5.26).