Стяжных и анкерных болтов
Наиболее распространённым видом крепёжных деталей в транспортных машинах являются болты метрические с шестигранной головкой (табл 11.5,6).
Болты (винты) изготавливают разных классов прочности, например из стали 35, класс прочности 5.6 (первое число, умноженное на 100, показывает предел прочности σВ = 500 Н/мм2; произведение чисел, умноженное на 10, определяет предел текучести σТ = 300 Н/мм2).
Пример условного обозначения болта с наружным диаметром метрической резьбы d = 6 мм, длиной l = 20 мм с крупным шагом резьбы, с полем допуска 8g, класса прочности 6.6 с покрытием 02 (кадмиевое с хроматированием) толщиной 9 мкм: Болт М6-8g×20.66.029 ГОСТ 7798-70.
Стандарты предусматривают и другие исполнения, в частности с резьбой до головки, а также различные варианты исполнений и нерекомендуемые диаметры и длины.
Пример обозначения болта с наружным диаметром метрической резьбы
d = 12 мм, с размером головки под ключ S = 18 мм, длиной l = 60 мм, с крупным шагом резьбы, поле допуска 6g, класса прочности 5.8, без покрытия:
Болт М12-6g×60.58(S18) ГОСТ 7805-70.
То же с размером под ключ S = 18 мм, с мелким шагом резьбы, поле допуска 6g, класса прочности 10.9, из стали 40Х, с покрытием 01 толщиной 6 мкм: Болт М12×1,25-6g×60.109.40Х.016 ГОСТ 7805-70.
Резьба – по ГОСТ 24705-81. Сбег и недорез резьбы – по ГОСТ 10549-80.
Технические требования – по ГОСТ 1759.0-87.
| Таблица 11.5 Болты с шестигранной головкой нормальные(ГОСТ 7787-70), и с уменьшенной головкой (ГОСТ 7808-70) | ||||||||
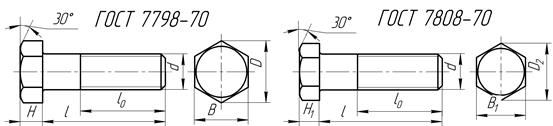
| ||||||||
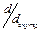
| Нормальные | С уменьш. головкой | l | l0 | ||||
| B | H | D | B1 | H1 | D2 | |||
| 8/6 | 5,5 | 14,2 | 13,2 | 8…60 | l0 = l при l ≤ 25, l0 = 22 при l ≥30 | |||
| 10/8 | 18,7 | 15,4 | 10…80 | l0 = l при l ≤ 30, l0 = 26 при l ≥35 | ||||
| 12/10 | 20,9 | 18,9 | 14…100 | l0 = l при l ≤ 30, l0 = 30 при l ≥35 | ||||
| 16/14 | 26,5 | 24,5 | 20…120 | l0 = l при l ≤ 40, l0 = 38 при l ≥45 | ||||
| 20/16 | 33,3 | 30,2 | 25…150 | l0 = l при l ≤ 50, l0 = 46 при l ≥55 | ||||
| 24/21 | 39,6 | 35,8 | 35…150 | l0 = l при l ≤ 60, l0 = 54 при l ≥65 | ||||
| Примечание. Размер l брать из ряда: 8, 10, 12, 14, 16, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 90, 100, 120, 130, 140, 150. |
–
| Таблица 11.6 Материалы резьбовых деталей и их допускаемые напряжения, МПа | |||||||
| Марка стали | Предел прочности σВ | Предел текучести, σT | Предел выносливости, σ-1р | Марка стали | Предел прочности σВ | Предел текучести, σT | Предел выносливости, σ-1р |
| Ст3 и 10 | 30Х | ||||||
| 20 | 40Х | ||||||
| 35 | 30ХГСА | ||||||
| 45 | ВТ16 | − | |||||
| Примечание. [τ] = 0,4σT для статической нагрузки; [τ] = (0,2…0,3)σТ для переменных нагрузок; [σсм] = 0,8σT для сталей; [σсм] = (0,4…0,5)σВ для чугунов |
Исходными данными для расчёта резьбовых соединений являются действующие в местах соединения нагрузки [5]. В результате расчёта определяется диаметр резьбы болта, обозначаемый его типоразмером.
В расчёте болтов сначала находят силу, приходящуюся на один болт [17]. Затем всё многообразие компоновок резьбовых соединений может быть сведено к трём простейшим расчётным схемам [44] (рис. 11.5…7).
Болт вставлен в отверстия с зазором (рис. 11.5).
Соединение нагружено продольной силой Q. Болт испытывает растяжение.
Условие прочности на растяжение запишется в виде: 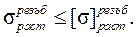
Напряжения растяжения в резьбе 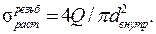
 Из условия прочности на растяжение находим внутренний диаметр резьбы болта
Из условия прочности на растяжение находим внутренний диаметр резьбы болта 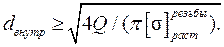
Найденный внутренний диаметр резьбы округляют до ближайшего большего по стандарту.
Болт установлен в отверстия без зазора.
Соединение нагружено поперечной силой Р. Болт работает на срез (рис. 11.6).
Внутренний диаметр резьбы рассчитывается аналогично случаю с растяжением: 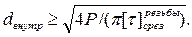
Порядок назначения номера (типоразмера по стандарту) болта аналогичен предыдущему случаю.
Болт установлен с зазором (рис. 11.7).
Соединение нагружено поперечной силой F.
При такой установке сила затяжки болта V должна дать такую силу трения между деталями, которая была бы больше поперечной сдвигающей силы F.
Болт работает на растяжение, а от момента затяжки испытывает ещё и кручение, которое учитывается повышением нормальных напряжений на 30 % (в 1,3 раза).
В расчётах принимают зависимость требуемой силы затяжки от сдвигающей поперечной силы F и коэффициента трения f (обычно f = 0,15) сила затяжки V =1,2 F/ f. Тогда внутренний диаметр резьбы болта
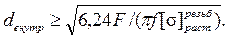
Во всех случаях в расчёте вычисляется внутренний диаметр резьбы, а обозначается резьба по наружному диаметру. Распространённая ошибка состоит в том, что рассчитав, например, внутренний диаметр резьбы болта 8 мм, назначают болт М8, в то время как следует назначить болт М10, имеющий наружный диаметр резьбы 10 мм, а внутренний 8 мм.
Концентрация напряжений во впадинах витков резьбы учитывается занижением допускаемых напряжений резьбы на 40% по сравнению с соответствующими допускаемыми напряжениями материала.
При проектировании редукторов и подобных механизмов наибольшую ответственность, а значит и наибольший интерес для проектировщика, представляет расчёт стяжных болтов, стягивающих между собой крышку и картер корпуса, а также болты крепления крышек подшипниковых узлов (рис. 11.8).
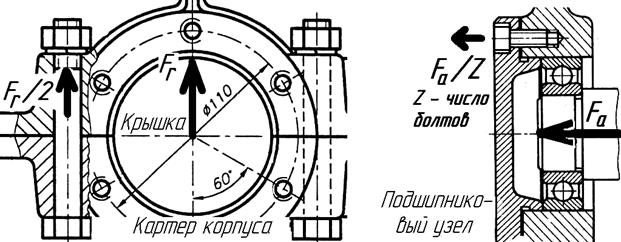
|
| Рис. 11.8. Болты крепления крышек |
Центрирование сопрягаемых деталей происходит либо штифтами (корпус), либо центрирующим посадочным пояском (подшипниковые узлы). Поэтому и те и другие болты установлены с зазором и нагружены растягивающей силой и крутящим моментом от затяжки гаечным ключом.
Для расчёта можно принять растягивающую силу болта в зависимости от радиальной Fr и осевой Fa реакций подшипников:
Q = Fr /2 – для каждого из стяжных болтов крышки корпуса;
Q= Fa/Z – для каждого из болтов крышки подшипникового узла (Z = 4 при диаметрах крышек до 100 мм, Z = 6 при диаметрах крышек более 100 мм).
Кручение болта учитывается повышением нормальных напряжений растяжения на 30 % (в 1,3 раза).
Тогда внутренний диаметр резьбы 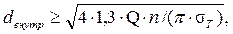
где n – коэффициент запаса прочности резьбы на растяжение, n = 3 для углеродистых сталей и n = 5 для легированных сталей.
Вычисленный внутренний диаметр впадин резьбы округляется до ближайшего большего по таблице стандартных болтов (табл. 11.5).
Полагая, что коэффициент трения в резьбе f = 0,15, назначим момент затяжки болта MЗАТ ≈ 0,2 ∙ Q ∙ d, где d − диаметр болта.
Проверочный расчёт на прочность ведётся по эквивалентным напряжениям при совместном растяжении и кручении σЭКВ = 1,3∙Q / S ≤ [σ]ЭКВ, где S – площадь опасного сечения болта S = πd2внутр/4; [σ]ЭКВ– допускаемое эквивалентное напряжение при неконтролируемой затяжке, Н/мм2:
для болтов диаметром до 16 мм [σ]ЭКВ = (0,2…0,25) σТ;
для болтов диаметром от 16 до 30 мм [σ]ЭКВ = (0,25…0,4) σТ.
В результате расчёта должны быть назначены: диаметр болта и момент затяжки. Например: "Для крепления крышки подшипникового узла применить 6 болтов М8 с моментом затяжки 7500 Н∙ мм".
В современных условиях гибких производственных и ремонтных технологий требуется частая замена и модернизация оборудования, для этого требуется частая переналадка, монтаж и демонтаж агрегатов и узлов. Оборудование для этого устанавливают на специальных фундаментных болтах, которые называют также анкерными болтами (от англ.: Anchor – якорь).
Фундаментный болт по ГОСТ 24379.1-80 состоит из шпильки, шайбы, гаек и других деталей. Шпильки изготавливают из углеродистой стали ВСт3пс2.
| Таблица 11.7 Размеры анкерных болтов различных типов, мм | ||||||||||||||

| ||||||||||||||
| С коническим концом (а) | ||||||||||||||
| d | D | l | H | D0 | При мощности двигателя | |||||||||
| М16 | 150…200 | 30…40 | 0,5…5 КВт | |||||||||||
| М20 | 200…250 | 40…50 | 5…40 КВт | |||||||||||
| М24 | 250…300 | 50…60 | 40…110 КВт | |||||||||||
| С коническим концом и разжимной цангой (б) | ||||||||||||||
| d | D | d1 | d1 | L | l | H | При мощности двигателя | |||||||
| М16 | 0,5…5 КВт | |||||||||||||
| М20 | 5…40 КВт | |||||||||||||
| М24 | 40…110 КВт | |||||||||||||
| С конической гайкой (в) | ||||||||||||||
| d | D | h | h0 | H | При мощности двигателя | |||||||||
| М16 | 150…200 | 0,5…5 КВт | ||||||||||||
| М20 | 200…250 | 5…40 КВт | ||||||||||||
| М24 | 250…300 | 40…110 КВт | ||||||||||||
| С изогнутым концом (г) | ||||||||||||||
| d = (М16, М20, М24); l1 = 8d ; l2 = 4d ; b = (6…8)d ; H ≈ 20d. | ||||||||||||||
Эти анкерные болты устанавливают в скважины, просверленные в полу цеха, или в колодец, специально предусмотренный в полу.
11.3. Расчёт соединения с натягом.
Посадка колеса на ось колёсной пары локомотива
Соединения деталей с натягом широко распространены в транспортном машиностроении. Образуются за счёт натяга, т.е. отрицательной разницы диаметров охватывающей детали (отверстия) и охватываемой детали (вала) до сборки. Соединения относят к неразъёмным, т.к. повторная сборка не обеспечит той же надёжности.
Наиболее типичным примером такого соединения является посадка колеса на ось колёсной пары подвижного состава.
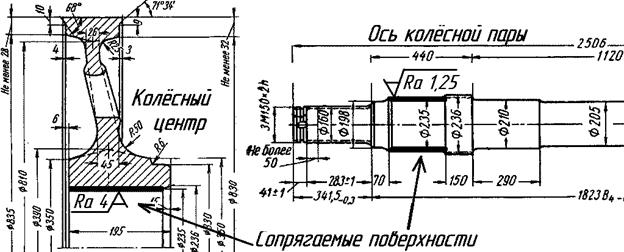
Рассмотрим расчёт такого соединения (рис. 11.9) на примере сопряжения колеса с осью ведущей колёсной пары тепловоза ТЭ3 [13, 42].
|
| Рис. 11.9. Сопрягаемые детали колёсной пары |
Самый тяжёлый режим – трогание состава. При этом тепловоз развивает тяговое усилие Qпуск = 41600 кГ = 407680 Н. Диаметр колеса d2 = 1050 мм, поэтому ведущие колёсные пары должны выдерживать вращающий момент Mпуск = Qпуск · (dкол /2) = 407680 · (235/2) = 107016000 Нмм. Тяга передаётся шестью редукторами, следовательно, на каждое колесо приходится вращающий момент Mпуск/12 = 8918000 Нмм. Колёсный центр изготовлен из стали 30Л, у которой предел текучести σТ = 250 МПа
Определяем коэффициент трения в зоне сопряжения венца и ступицы (табл. 11.8). Поскольку в рассчитываемом сопряжении Ra1 = 1,25, а Ra2 = 4,0, принимаем для сопряжённых стальных деталей f = 0,10.
Задаёмкоэффициент запаса сцепления К = 1,2...2. Принимаем К = 2 для тягового подвижного состава.
Вычисляем минимальное контактное давление на сопрягаемых поверхностях деталей. Для передачи требуемого момента при длине посадочного участка l = 180 мм давление должно быть равно
pkmin = 2K·Mпуск/(fπd22l) = 2·2·8918000/(0,10·3,14·2352·180) = 10,7 МПа.
Коэффициент Пуассона μ для стали ≈ 0,3.
Модуль упругости стали принимаем E1 = E2 = 20·104 МПа
| Таблица 11.8 Коэффициент трения для цилиндрических сопряжений с натягом | ||||||
| Материал охватывающей детали | Высота микронеров- ностей, Ra1 | Материал охватываемой детали | Высота микронеров- ностей, Ra2 | Давление, МПа | Коэффициент трения | |
| Сталь | 1...1,25 | Сталь | 1...1,25 3,2...4,0 | > 6 | 0,12 0,10 | |
| Чугун серый | 1...1,25 | Сталь | 1...1,25 3,2...4,0 | > 6 | 0,08 0,075 | |
| Бронза | 1...1,25 | Чугун серый | 1...1,25 | – | 0,07 | |
| Магниево-алюминиевые сплавы | – | Стали 30...50 | – | – | 0,03...0,09 | |
| Латунь | – | Стали 30...50 | – | – | 0,04...0,1 |
| Таблица 11.9 Модули упругости и коэффициенты линейного температурного расширения для некоторых материалов | |||
| Материал | E·104 МПа | α ·10-6 [1/ºС] | |
| нагрев | охлаждение | ||
| Сталь и стальное литьё | 20...21 | – 8,5 | |
| Чугунное литьё σПЧ.Р < 200 МПа | 7,5...10,5 | – 8 | |
| Ковкий чугун | 9...15 | – 8 | |
| Медь | 12,5 | – 14 | |
| Бронза оловянная | 8,5 | – 15 | |
| Латунь | – 16 | ||
| Алюминиевые сплавы | 6,5...7,5 | – 18 | |
| Магниевые сплавы | 3,6...4,7 | – 21 | |
| Пластмассы | 0,4...1,6 | 46...70 | – |
Вычисляем коэффициенты радиусов, учитывая, что ось не имеет отверстия в центре (r1=0), а наружный радиус ступицы колеса r3 = 350/2 = 175 мм
С1 = (r22+r12)/(r22–r12) – μ1 = (117,52 + 0)/(117,52 – 0) – 0,3 = 0,7;
С2 = (r32+r22)/(r32–r22) + μ2 = (1752 + 117,52)/(1752 – 117,52) – 0,3 = 2,342.
Определяем минимальный расчётный натяг
Δmin= pkmind2(С1/Е1+С2/Е2) = 10,7∙235(0,7/20∙104+2,342/20∙104) = 38,4 ≈ 40 мкм.
Вычисляем поправку на неровность поверхностей
uR ≈ 1,2(Ra1+Ra2) = 1,2(1,25+4,0) = 5,1 ≈ 6 мкм.
Вычисляем поправку на разность температур. Колесо при сборке нагревают до tp1 = 200 °С, а ось не нагревается (tp2 = 20 °С). Коэффициенты температурного линейного расширения для сталей при нагреве примем α1 = α2 = 11·10−6 [1/°С]. Тогда поправка на разность температур ut = (α1tp1 – α2tp2)d2 =
= (11 · 10−6 · 200 − 11 · 10−6 · 20) · 235 = 0,04653 мм ≈ 47 мкм.
Минимальный табличный натяг с учётом всех технологических факторов равен ΔТmin = Δmin + uR + ut = 40 + 6 + 47 = 93 мкм.
Назначаем посадку в системе отверстия (табл. 11.10). Для посадочного диаметра 235 мм: Æ235P9/p6 с полем допуска вала p6 (+50+79) и полем допуска отверстия P9 (–165–50). Такая посадка обеспечит натяг в диапазоне от минимального Δmin = 50 + 50 = 100 мкм ( больше, чем ΔТmin = 93 мкм) до максимального Δ max = 79 + 165 = 244 мкм.
Проверяем прочность соединения при контактном давлении, соответствующем максимальному натягу
pkmax = pkminΔ max /ΔТmin = 10,7·244/93 = 28,1 МПа.
Вычисляем эквивалентные напряжения для опасных точек посадочной поверхности ступицы колеса
σэкв = pkmax 2r32/(r32– r22) = 28,1·2·1752/(1752–117,52) = 102,3 МПа.
Коэффициент запаса прочности nступ = σТ /σэкв = 250/102,3 = 2,44.
Прочность оси не проверяется, поскольку в её центре отверстий нет.
Таким образом, можем сделать заключение о достаточной прочности соединения.
В качестве дополнительного примера рассмотрим расчёт посадки венца (рис. 11.10) на чугунную ступицу червячного колеса редуктора механизма перемещения пакетов пути моторной платформы МПД [26, 33].
 Венец выполнен из бронзы БрА9ЖЗЛ, отливка в землю (σТ = 200 МПа, табл. 3.2); ступица из серого чугуна СЧ15 (σПГ.Р = 118 МПа; μ = 0,25). Сборка без нагрева напрессовкой.
Венец выполнен из бронзы БрА9ЖЗЛ, отливка в землю (σТ = 200 МПа, табл. 3.2); ступица из серого чугуна СЧ15 (σПГ.Р = 118 МПа; μ = 0,25). Сборка без нагрева напрессовкой.
Мощность, передаваемая червячным колесом N2 = 12 кВт и частота его вращения n2 = 50 об/мин. Необходимо проверить прочность соединения, т.е. не вызовет ли заданная нагрузка проворачивание венца на ступице.
Находим вращающий момент на колесе
M2 = 30N2 / (π·n2) = 30·12·103/(3,14 ·50) = 2,3·103 Нм.
Коэффициент трения в зоне сопряжения венца и ступицы (табл. 11.8) выбираем для бронзы по чугуну f = 0,07.
Принимаем коэффициент запаса сцепления К =1,2 для заданной нагрузки.
Минимальное контактное давление на сопрягаемых поверхностях деталей при длине посадочного участка l = 50 мм для передачи требуемого момента должно быть
pkmin = 2K·M2 / (fπd22l) = 2 ·1,2 ·2,3 ·103 ·103 / (0,07 ·3,14 · 2002 ·50) = 12,5 МПа.
Модули упругости для чугунной ступицы и для бронзового венца принимаем E1 = Eчуг = 10·104 Н/мм2; E2 = Eброн = 8,5 ·104 МПа.
Коэффициент Пуассона μ для чугуна ≈ 0,25; для бронзы и латуни ≈ 0,32.
Дата добавления: 2020-06-09; просмотров: 655;











