Декартово произведение

Эта операция не накладывает никаких ограничений на схемы исходных отношений, и поэтому она допустима для любых двух отношений.

Под декартовым произведением двух отношений понимается множество упорядоченных пар кортежей. Пусть имеются два отношения г и s, тогда отношение t = г * s арности к = к! + k₂к1 - арность r, a k2— арность s, называется декартовым произведением г и s, если оно состоит из кортежей, первые k_! компонентов которых образуют кортежи из г, а остальные k2 — из s.

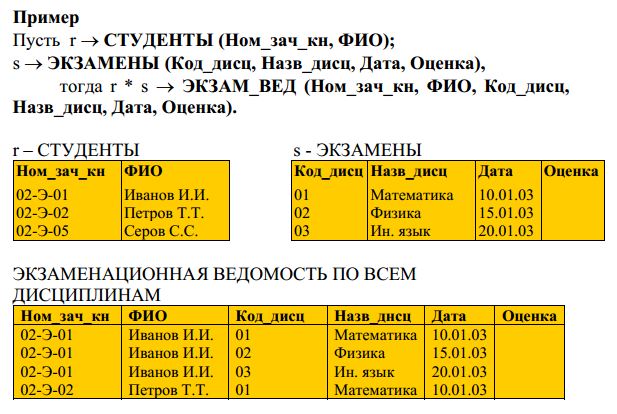
Пересечение

Пусть имеются два отношения r и s , тогда отношение t = r ∩ s называется пересечением r и s, если каждый кортеж, принадлежащий t, одновременно принадлежит r и s. Операция применяется к отношениям одной арности. Справедлива следующая формула: t = r ∩ s = r - (r - s).

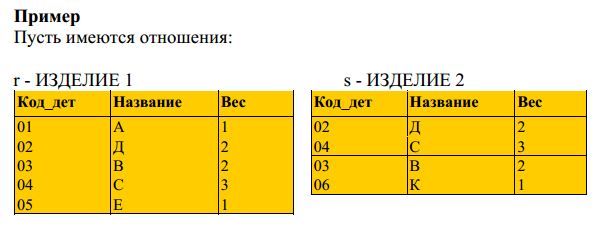
Сформируем ответ на такой запрос: определить детали, входящие в
состав обоих изделий. Для этого необходимо выполнить операцию
пересечения двух исходных отношений. Результат представляется
отношением:

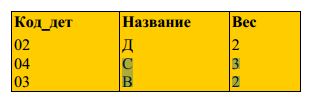
Проекция (Project)

Оператор проекции (вертикальное подмножество) является унарным
оператором на отношениях. Он осуществляет выбор на множестве
столбцов.

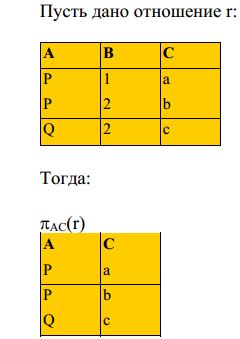
Пусть в отношении r(R) выделено некоторое множество атрибутов
Y, тогда отношение t = πY(г) называется проекцией отношения r, если оно
является вертикальным подмножеством столбцов отношения r из
множества R.

Иными словами, проекция R на Y есть также отношение, полученное
вычеркиванием столбцов, соответствующих атрибутам R — Y, и исключением, по определению отношения, из оставшихся столбцов повторяющихся строк.

Выбор (Select)

Выбор или селекция — это одна из важнейших операций обработки
информации. Она также как и предыдущая, относится к унарным
операциям над отношением. Результатом ее применения к отношению r
является другое отношение, которое представляет собой подмножество
кортежей отношения r, с определенным значением в выделенном атрибуте.

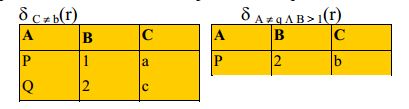
Итак, результатом селекции отношения r по некоторому Θ будем
считать отношение t = δΘ (г), которое включает в себя кортежи отношения
r, удовлетворяющие указанному условию Θ.

Условие Θ — это формула, по которой определяется выборка.
Операндами в такой формуле являются атрибуты отношения, а знаками
операций — логические операции и операции отношений.

Соединение (Join)

Пусть имеются два отношения r (X, У) и s (Y, Z) и некоторое условие
Θ, где X, У, Z-— непересекающиеся множества атрибутов и Y—
множество атрибутов, общих для r и s, тогда отношение
t = r >Θ< s называется Θ-соединением r и s, если каждый кортеж,
принадлежащий t, состоит из кортежей r и s, при выполненном условии Θ.
Справедлива следующая формула: t = δΘ (r * s), то есть Θ-соединение представляет собой декартово произведение r и
s, над которым выполнена селекция по условию Θ.

Пример

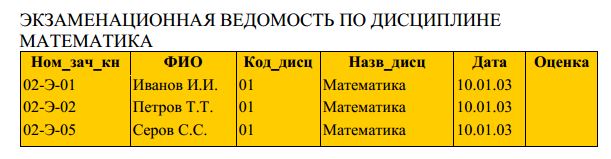
Из общей экзаменационной ведомости по всем дисциплинам
получим экзаменационную ведомость по дисциплине математика. Для
этого выполним операцию соединение (Join) при условии Код_дисц = “01 ”

Деление

Деление — это также бинарная несимметричная операция для
получения некоторого отношения из двух исходных, причем степень
результирующего отношения не совпадает со степенью ни одного из
операндов, а вычисляется как разность между степенью отношения
делимого и степенью отношения-делителя.

Пусть имеются отношения r(Х, У) арности k1 и p(Z) арности k2, где Y
и Z определены на одном домене, тогда отношение t = r ÷ p арности k1 – k2
называется делением r на p, если любой кортеж из t вместе с любым
кортежем из p образуют кортеж, имеющийся в r.

Пример
Даны отношения, содержащие сведения об экзаменах, которые
должны были сдавать студенты, и сведения о результатах сдачи этих
экзаменов:

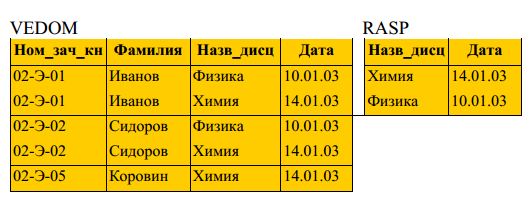
Сформируем ответ на такой запрос: дать сведения о студентах,
сдавших все экзамены. Для получения ответа на данный запрос
необходимо выполнить следующую операцию деления:
t = r ÷ p