МИНИМИЗАЦИЯ ЧИСЛА ВНУТРЕННИХ СОСТОЯНИЙ ПОЛНОСТЬЮ ОПРЕДЕЛЕННЫХ АВТОМАТОВ.

Рассмотрим метод минимизации полностью определенных автоматов, предложенный Ауфенкампом и Хоном.

Основная идея этого метода заключается в разбиении всех состояний исходного абстрактного автомата на попарно непересекающиеся классы эквивалентных состояний и замене каждого класса эквивалентности одним состоянием. Т.о. получающийся в результате минимальный автомат имеет столько состояний, на сколько классов эквивалентности разбиваются состояния исходного автомата.

Для пользования методом введем несколько определений.

Два состояния абстрактного автомата называются 1-эквивалентными в том случае, если реакции автомата в этих состояниях на всевозможные входные слова совпадают.

Объединение всех 1-эквивалентных состояний абстрактного автомата образует 1-класс эквивалентности.

1-эквивалентные состояния автомата называются 2-эквивалентными, если они переводятся любым входным сигналом также в 1-эквивалентные состояния.

Объединение всех 2-эквивалентных состояний образует 2-класс эквивалентности.

По индукции можно распространить определение до i-эквивалентных состояний и i-классов эквивалентности.

Если для некоторого i разбиения состояний автомата на ( i +1) - классы совпадает с разбиением на i-классы, то оно является разбиением и на ¥ - классы эквивалентности.

Разбиение множества внутренних состояний автомата на ¥ - классы и является требуемым разбиением на классы эквивалентности, при этом такое разбиение может быть получено за конечное число шагов.

Все вышеизложенное непосредственно применимо к минимизации автомата Мили. При минимизации полностью определенных автоматов Мура вводится понятие 0-эквивалентности состояний и разбиение множества состояний на 0-эквивалентные классы: к такому классу относятся одинаково отмеченные состояния автомата Мура.

Если два 0-эквивалентных состояния любым входным сигналом переводится в два 0-эквивалентных состояния, то они называются 1-эквивалентными. Все дальнейшие классы эквивалентности состояний для автомата Мура определяются аналогично приведенному для автоматов Мили.

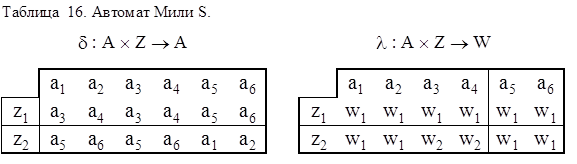
Рассмотрим пример минимизации автомата Мили, заданного таблицами переходов и выходов :

Из таблицы выходов получаем разбиение на 1-классы эквивалентности p₁, объединяя в эквивалентные классы Bi состояния с одинаковыми столбцами:

p₁ = {B₁, B₂}; B₂ = {a₁, a₂, a₅, a₆}; B₂ = {a₃, a₄}

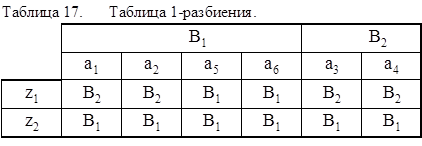
Для получения 2-эквивалентных состояний строим таблицу 1-разбиения (табл.17), заменяя в таблице переходов состояния a₁ соответствующими классами эквивалентности B1 или B2.

Из полученной таблицы 1-разбиения получаем 2-классы эквивалентности C_i и разбиение p₂ = {C₁, C₂, C₃}, где С₁ = {a₁, a₁}, C₂ = {a₅, a₆}, C₃ = {a₃, a₄}. Сравнивая p₂ и p₁, отмечаем, что эти разбиения отличаются друг от друга. Поэтому аналогично строим таблицу 2-разбиения (табл. 18), опять заменяя в таблице переходов состояния a_i соответствующими классами эквивалентности C_i.

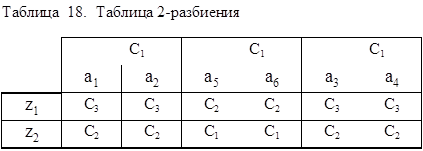
Из полученной таблицы 2-разбиения получаем 3-классы эквивалентности D_i и разбиение p₃ ={ D₁, D₂, D₃}, где D₁ = {a₁, a₂}, D₂ = {a₅, a₆}, D₃ = {a₃, a₄}.

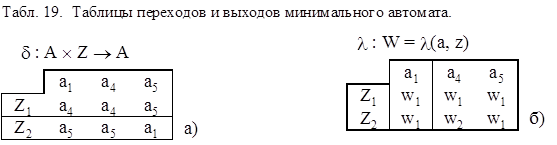
Сравнивая p₃ и p₂, замечаем, что D₁ = C₁, D₂ = C₂, D₃ = C₃, p₃ = p₃. Следовательно получили разбиение на ¥- эквивалентные классы. Т.к. всего три таких класса, то минимальный автомат будет содержать всего три состояния. Выбираем из каждого класса D_i по одному состоянию и получаем множество состояний A' минимального автомата. Пусть, например, A'={a₁, a₄, a₅}. Для получения минимального автомата из первоначальных таблиц переходов и выходов (табл. 16) вычеркиваем столбцы, соответствующие "лишним состояниям" a₂, a₃, a₆. В результате получается минимальный автомат Мили, эквивалентный исходному автомату (табл. 19).

Минимизацией числа внутренних состояний автомата заканчивается этап абстрактного синтеза.