Упругие элементы передних и задних подвесок

На рис. 166 изображена колебательная система - кузов автомобиля подрессоренной массой М_п, опирающийся на упругие элементы передних и задних подвесок.

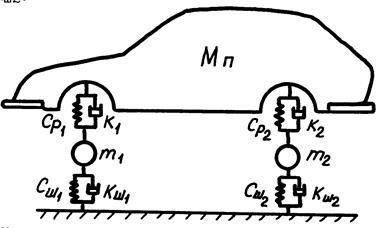
Рис. 166. Колебательная система - кузов автомобиля на колесах

На рис. 166 обозначены: коэффициенты сопротивления амортизаторов – К₁ и К₂ , массы колес – m₁ и m ₂, жесткости шин – С_ш1 и С _ш2 , коэффициенты внутреннего трения шин – К_ш1 и К _ш2 , жесткости рессор – С_р1 и С _р2 .

При расчетах колебаний автомобиль может быть представлен в виде балки, опирающейся на два упругих элемента – передние и задние рессоры автомобиля (рис. 167).

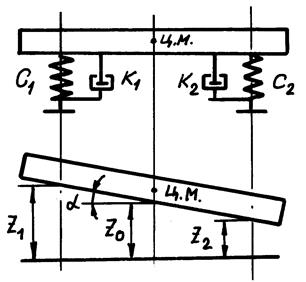
Рис. 167. Модель автомобиля

Вертикальные перемещения и поворот балки на упругих элементах с жесткостями С₁ и С₂, представляющей собой модель автомобиля, можно выразить уравнениями:

вертикальные силы, действующие на кузов

М _п × 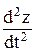+ C₁ × z ₁ + C ₂ × z₂ = 0; (104)

продольные моменты, действующие на кузов относительно центра масс

M _п ×r ² × 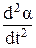– C₁ × z ₁ × L₁ + C ₂ × z ₂ × L ₂ = 0, (105)

где М _п - подрессоренная масса; z ₁ - перемещение балки над передним упругим элементом; z ₂ - перемещение балки над задним упругим элементом; a - угол поворота балки; L₁ - расстояние от центра масс балки до середины переднего упругого масс балки; L₂ – расстояние от центра масс балки до середины заднего упругого элемента; r - радиус инерции; z - перемещение центра масс балки.

Выразив из рис.163 перемещения z₁ = z + a×L₁ и z ₂ = z - a × L ₂ и продифференцировав их дважды, запишем:

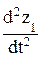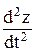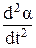= + × L₁ . и 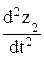= 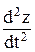+ 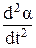× L₂ . (106)

Подставив в уравнения (104) и (105) правые части из выражений (107) после преобразований получим:

М_п 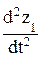+ C₁ × z ₁ × (1 + 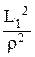) + C ₂ × z₂× (1 – 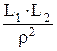) = 0 ; (107)

М_п 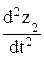+ C₂ × z ₂ × (1 + 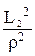) + C₁ × z₁× (1 – 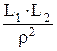) = 0 . (108)

Поделив эти уравнения на М_п, запишем:

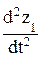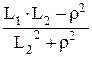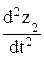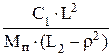+ × + × z₁ = 0 ; (109)

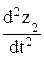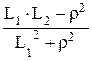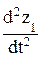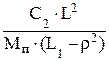+ × + × z₂ = 0 . (110)

Обозначим выражения:

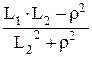= m ₁ и 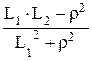= m ₂ ,

где m ₁ , m ₂ – коэффициенты связи колебаний передней и задней частей автомобиля.

В уравнениях (119) и (111) обозначим:

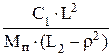= w₁² ; 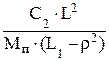= w₂² ,

где w₁ и w₂ –частоты колебаний передней и задней частей автомобиля без учета взаимной связи колебаний (парциальные частоты).

Характеристическим для системы уравнений с использованием m и w является уравнение вида:

W⁴ – (w₁² + w₂²) × 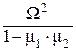+ 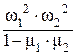= 0 . (111)

Решая это биквадратное уравнение, можно получить выражение для определения частот связанных колебаний:

Для высокой частоты колебаний

W₁ = 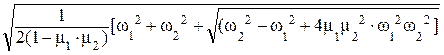; (112)

Для низкая частота колебаний

W₂ = 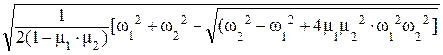. (113)

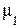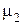Если в выражениях (110) и (111) L₁ × L ₂ = r², то коэффициенты связи и равны нулю. Тогда колебания передней и задней частей кузова автомобиля оказываются не связаны между собой: каждая из них колеблется со своей частотой, называемой парциальной, которая рассчитывается по выражению

w = .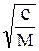

Для легковых и грузовых автомобилей отношение r² / (L₁ × L ₂) близко к единице. Поэтому колебания передней и задней частей этих автомобилей считаются не связанными между собой. Для автобусов это отношение может приближаться к 2, вследствие чего взаимное влияние подвесок автобусов необходимо учитывать. Если

0,8L₁× L ₂ < r² < 1,2L₁ × L ₂ ,

частоты связи W и парциальные частоты w₁ и w₂ отличаются лишь на 5...6 % . Таким образом, на величину W и w влияет положение центра тяжести, момент инерции подрессоренной части автомобиля и отношение статических прогибов передней и задней подвесок.