Поперечная устойчивость автомобиля

Устойчивость – способность автомобиля двигаться без скольжения и опрокидывания.

Потеря устойчивости может наступить на дороге с поперечным или продольным уклоном, на закруглении дороги, при боковом ветре, торможении, интенсивном разгоне и т.д. Под действием появляющихся сил сначала теряется сцепление колес с дорогой, а далее происходит опрокидывание автомобиля.

Различают поперечную и продольную устойчивость автомобиля. Наиболее часто и с более тяжелыми последствиями бывает потеря поперечной устойчивости, а именно - опрокидывание автомобиля. Поэтому автомобили делаются так, чтобы боковое скольжение на закруглениях дорог наступало раньше, чем опрокидывание и служило водителю предупреждением о необходимости снизить скорость.

Предельная скорость движения автомобиля на закруглении дороги, имеющей поперечный уклон к центру закругления, при которой боковое скольжение отсутствует, может быть определена следющим образом. Боковое скольжение не произойдет до тех пор, пока поперечная сила сцепления колес будет больше или равна, чем центробежная сила, действующая на автомобиль. Из равенства этих сил можно найти предельную скорость автомобиля.

Поперечная сила сцепления (рис. 106)

Р_сц = (G_а × соs b + P_j × sin b) × j ,

где G_a - сила тяжести автомобиля; P_j - центробежная сила (сила инерции) автомобиля.

Рис. 106. Движение автомобиля на повороте

Сила Р_ск, вызывающая скольжение автомобиля

Р_ск = P_j × сos b - G_a × sin b .

Если (G_a × сos b + P_j × sin b) × j ³ P_j × сos b - G_a × sin b, скольжение колёс отсутствует.

Подставив выражение для определения P_j = (G_a/q ) × ( V²/R ), и решая составленную зависимость, выразим предельную скорость автомобиля из условия отсутствия бокового скольжения:

V_{пр. ск.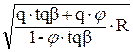} = , (73)

где V_{пр. ск.} - предельная скорость на повороте, при которой поперечное сколь- жение отсутствует; q - ускорение свободного падения; b - угол поперечного уклона профиля дороги; R - средний радиус траектории движения автомобиля на закруглении; j - коэффициент сцепления колеса и дороги.

Если знаменатель в этом выражении равен нулю, боковое скольжение отсутствует при любой скорости:

1 - j × tq b = 0 , V_{пр. ск.} = ¥.

Угол поперечного уклона дороги в этом случае можно найти из условия

tq b = 1/j . Так определяется поперечный уклон для скоростного трека.

При отсутствии поперечного уклона (b = 0) выражение приобретает вид:

V_{пр ск .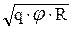} = . (74)

Опрокидывание автомобиля не произойдет, если момент от центробежной силы, действующий относительно пятна контакта колес (т.А на рис. 106) во внешнюю сторону, меньше, чем сумма моментов сил, действующих в обратном направлении:

P_j × сos b × h _g £ P_j × sin b × l /2 + G_a × сos b × l /2 + G_a × sin b × h _g ,

где h _g - высота расположения центра масс автомобиля; l - колея автомобиля.

Решая это уравнение аналогичным предыдущему случаю способом, получим выражение для определения предельной скорости автомобиля, при которой он может двигаться на заданном закруглении дороги без бокового опрокидывания:

V_{пр. опр.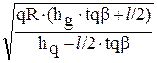} = . (75)

Если знаменатель равен нулю, V_{пр. опр.} = ¥ , т.е.

h _g = l/2 × tq b или tq a = 2 h_g / l.

При этом условии исключается опрокидывание автомобиля, движущегося с любой скоростью. Чтобы скорость, при которой наступает боковое скольжение на горизонтальной дороге, была ниже, чем при опрокидывании, необходимо:

_________ _____________

Ö q × j × R £ Ö q × R × l / 2h_g .

Oтсюда, чтобы не было опрокидывания, отношение колеи автомобиля к высоте расположения центра масс должно быть: l /2h_g ³ j .

Способствуют поперечному опрокидыванию автомобиля упругие элементы подвески, снижающие расчетную скорость, при которой наступает опрокидывание автомобиля, на 10...12%.

Электронная система управления подвеской колес на современном автомобиле позволяет путем увеличения жесткости на повороте уменьшить угол крена автомобиля. Система стабилизации ограничивает также скорость автомобиля, что дает возможность исключить занос.