Индукционный цифровой датчик углового перемещения

На рисунке 2.12 показана структурная схема датчика следящего уравновешивания с обратной связью по результату измерения.

Рисунок 2.12

Датчик состоит из вращающегося трансформатора с блоком питания (БП), функционального преобразователя (ФП), фильтра (Ф), корректирующего звена (КЗ), преобразователя напряжение – частота (ПНЧ) и реверсивного счетчика (РСч).

Ось ротора вращающегося трансформатора кинематически связана с осью выходного вала системы. Напряжение питания 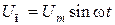, где U_m – амплитудное значение напряжения питания, 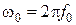– угловая частота, f₀ – частота питающего напряжения, которое подается на однофазную роторную обмотку. При повороте ротора на угол j_вых на статорных обмотках формируются сигналы, амплитуды которых являются функциями угла поворота

,

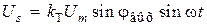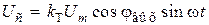, (2.24)

где k_T – коэффициент трансформации вращающегося трансформатора.

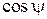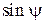Напряжения U_S и U_C подаются на функциональный преобразователь ФП, в котором реализуется операция умножения их на функцию и , где – угловой эквивалент кода :

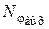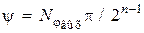, (2.25)

где n – число разрядов реверсивного счетчика.

Одновременно на функциональный преобразователь ФП подается напряжение питания 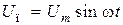, которое используется для реализации функции |sinwt|. В результате, на выходе функционального преобразователя формируется сигнал

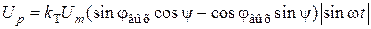, (2.26)

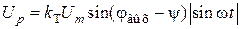. (2.27)

Пульсации напряжения U_р сглаживаются фильтром и через корректирующее звено КЗ подаются на вход преобразователя напряжение – частота ПНЧ. Выходной сигнал ПНЧ представляет собой последовательность импульсов, частота которых пропорциональна входному напряжению.

При положительном знаке входного напряжения последовательность импульсов формируется на одном выходе ПНЧ, а при отрицательном знаке – на другом. Эти импульсы поступают на суммирующий или вычитающий входы реверсивного счетчика РСч, который формирует код 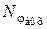, эквивалентный углу поворота j_вых.

Код 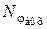используется в функциональном преобразователе для изменения значения 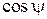и 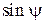, таким образом, чтобы напряжение U_р на его выходе устанавливалось равным нулю. Согласно уравнению (2.27), это означает, что измеренное значение угла поворота 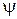равно фактическому значению j_вых.

Описанная измерительная система относится к классу следящих, а ее режим работы называют режимом следящего уравновешивания измеренного и фактического значений угла поворота. Точность уравновешивания зависит от астатизма измерительной системы, который обеспечивается корректирующим звеном КЗ. Промышленность выпускает цифровые датчики положения с астатизмом первого и второго порядков. Датчики обладают высоким быстродействием, практически не чувствительны к пульсациям частоты питающего напряжения и к внешним возмущениям.

Погрешность цифрового датчика с вращающимся трансформатором характеризуется величиной средней квадратической ошибки

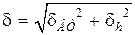, (2.28)

где d_ВТ – асимметрия нулевых точек вращающегося трансформатора;

d_h – средняя квадратическая погрешность реверсивного счетчика, форми-
рующего код 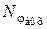, которую определяют по формуле

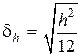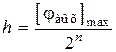, . (2.29)

Число разрядов счетчика n определяют из условия согласования точности преобразования сигнала в код с погрешностью вращающегося трансформатора (d_h = d_ВТ):

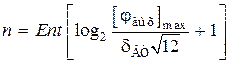, (2.30)

где Ent – символ целой части.

Пример.Определить требуемую разрядность АЦП индуктивного цифрового датчика угла поворота и среднюю квадратическую погрешность датчика при следующих исходных данных: максимальный угол поворота [j_вых]_max = 60^о; асимметрия нулевых точек вращающегося трансформатора d_ВТ= ±10 угловых минут.

Решение.

Число разрядов реверсивного счетчика

.

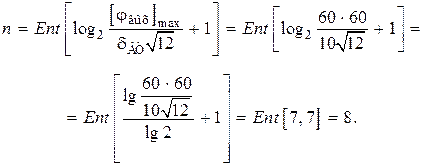Шаг квантования по уровню

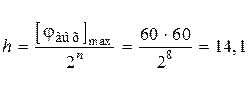угловых минут.

Средняя квадратическая погрешность квантования

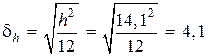угловых минут.

Средняя квадратическая погрешность цифрового датчика

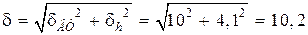угловых минут.

Видно, что причиной погрешности цифрового датчика является прежде всего погрешность измерительного преобразователя (ВТ). Поэтому в цифровых датчиках перемещений применяют многополюсные вращающиеся трансформаторы.

Пример.Пусть ВТ имеет 5 пар полюсов (р_п = 5) и асимметрия нулевых точек d_ВТ = ± 2 угловые минуты. Тогда для условий предыдущей задачи получим:

Число разрядов реверсивного счетчика

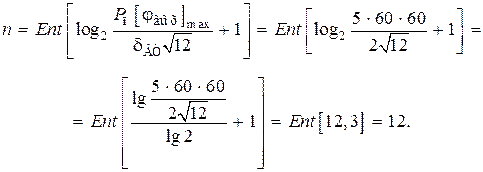
Шаг квантования по уровню

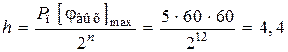угловых минут.

Средняя квадратическая погрешность квантования

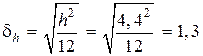угловых минут.

Средняя квадратическая погрешность цифрового датчика

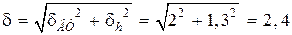угловых минут.