Акустические датчики
Звуковые волны проявляются, главным образом, через вызываемые ими изменения давления и скорости.
Остановимся на основных понятиях и подходах к рассматриваемому вопросу.
5.12.1. Распространение плоской волны
Для физического описания течения используются законы:
- сохранения массы и количества движения;
- уравнение состояния.
С помощью этих соотношений можно получить, что возмущения малой амплитуды распространяются со скоростью, выражаемой по формуле:
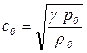 , (5.140)
, (5.140)
где 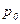 - среднее давление;
- среднее давление;
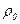 - средняя плотность среды;
- средняя плотность среды;
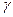 - отношение теплоемкостей при постоянном давлении и объеме.
- отношение теплоемкостей при постоянном давлении и объеме.
Это распространение возмущения сопровождается изменением давления, скорости, плотности, и температуры.
Плоская гармоническая волна
Уравнение для давления плоской синусоидальной волны, распространяющейся вдоль положительного направления оси OX, имеет вид
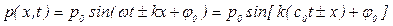 , (5.141)
, (5.141)
где 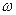 - круговая частота;
- круговая частота;
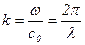 - волновое число (
- волновое число ( 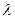 - длина волны);
- длина волны);
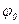 - начальная фаза колебаний точек среды;
- начальная фаза колебаний точек среды;
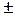 - распространение волны вдоль положительного или отрицательного направления оси OX.
- распространение волны вдоль положительного или отрицательного направления оси OX.
Существует и экспоненциальная форма записи уравнения плоской волны (эквивалентная синусоидальной форме):
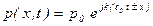 (5.142)
(5.142)
Данная форма записи удобна для дифференцирования.
Получим выражение для скорости волны 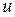 .
.
Для этого используем линеаризованное уравнение динамики (из закона сохранения количества движения, уравнение динамики, связывающее градиент давления 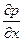 и производную скорости по времени
и производную скорости по времени 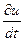 )
)
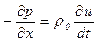 . (5.143)
. (5.143)
Вводя оператор 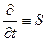 , приходим к удобному выражению
, приходим к удобному выражению
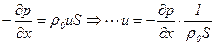 .
.
Отсюда после очередной замены 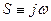 (переходим в частотную область) из (5.144) получим
(переходим в частотную область) из (5.144) получим
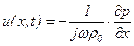 .
.
Продифференцировав (5.142), подставив результат в правую часть последнего выражения и производя последующую замену 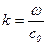 , приходим к выражению
, приходим к выражению
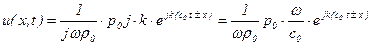 .
.
Перепишем окончательное выражение для скорости
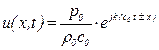 , (5.144)
, (5.144)
которое устанавливает связь между скоростью волны, давлением и плотностью среды.
Переносимая волной интенсивность звука 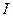 (средний поток звуковой энергии на единицу площади) выражается с помощью осредненного во времени произведения давления на скорость
(средний поток звуковой энергии на единицу площади) выражается с помощью осредненного во времени произведения давления на скорость
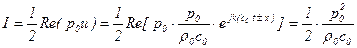 , (5.145)
, (5.145)
где 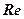 - реальная часть в комплексных выражениях зависимостей.
- реальная часть в комплексных выражениях зависимостей.
Из последнего соотношения следует, что интенсивность звука при распространении волны полностью описывается давлением.
Произвольная плоская волна
Плоскую волну можно получить, возбуждая цилиндрическую трубку конечной длины с помощью поршня, колеблющегося, например, вдоль оси OX.
На торце поршня происходит отражение возмущения, и поле давления можно описать следующим образом по аналогии (5.142)
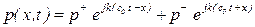 (5.146)
(5.146)
Величины 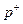 и
и 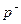 - составные части амплитуды падающего и отраженного волн.
- составные части амплитуды падающего и отраженного волн.
Поле скорости получаем из уравнения динамики (вида 5.144)
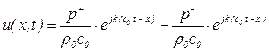 , (5.147)
, (5.147)
Выражения (5.146) и (5.147) показывают, что изменения амплитуды давления 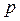 и скорости
и скорости 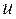 происходят не синфазно, а зависят от абсциссы x.
происходят не синфазно, а зависят от абсциссы x.
Интенсивность 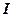 вычисляется по выражению (по аналогии (5.145))
вычисляется по выражению (по аналогии (5.145))
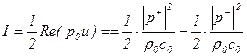 , (5.148)
, (5.148)
Как следует из последнего выражения, значение интенсивности не зависит от x и представляет собой разность между падающим и отраженным потоками.
5.12.2. Распространение трехмерной волны
Волны в этом случае не являются плоскими и происходит уменьшение амплитуды с увеличением расстояния от источника до точки наблюдения (что следует из закона сохранения энергии).
Рассмотрим случай сферического источника с пульсирующим потоком энергии 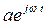 .
.
В этом случае имеют место следующие соотношения:
- давление
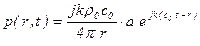 ; (5.149)
; (5.149)
- скорость
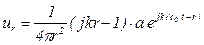 , (5.150)
, (5.150)
- интенсивность
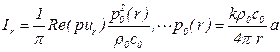 , (5.151)
, (5.151)
Из этих выражений видно, что радиальная составляющая интенсивности убывает обратно пропорционально квадрату расстояния от источника при любых 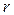 .
.
5.12.3. Микрофоны
Из названных в предыдущих разделах механических величин, характеризующих звуковые волны можно измерить только давление, а скорости частиц, соответствующие звуковым волнам, слишком малы и, следовательно, их нельзя измерить обычными анемометрами, используемых при исследовании жидкостей.
Однако компоненты скорости звука можно определить косвенным образом с использованием уравнения динамики, связывающего градиент давления и производную скорости по времени (см. (5.143))
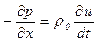 .
.
Эту операцию можно произвести, используя датчик, применяемый для измерения разности давлений. Этот датчик, основанный на измерении градиента давления, называется микрофоном.
Другой часто используемый метод состоит в обработке с помощью электроники разности сигналов с двух микрофонов.
5.12.3.1. Принцип действия микрофона
Микрофон представляет собой датчик, преобразующий акустический сигнал в электрический.
Классическим можно считать микрофон, применяемый в телефонной трубке.
Основан на необратимом явлении, под действием давления происходит изменение сопротивления контакта частиц угля, заполняющих объем, закрытый мембраной.
Но микрофон этого типа не приспособлен для физических измерений, т.к. имеет ограниченную полосу пропускания.
Для создания измерительных микрофонов предпочтительнее методы преобразования, основанные на обратимых явлениях электромагнитного, электростатического, пьезоэлектрического типов.
5.12.3.2. Основные типы микрофонов
Выделяются группы микрофонов, предназначенных для измерения:
- давления;
- градиента давления.
Первые осуществляют физические измерения давления, вторые - физические измерения скорости звука.
Важное преимущество последних – их чувствительность к направлению распространения.
Для получения более выраженной направленности можно использовать микрофоны, чувствительные ко второму градиенту.
 5.12.3.3. Электро-механо-акустические аналоги
5.12.3.3. Электро-механо-акустические аналоги
Аналогия “течение – ток”
Сопоставляя уравнения для электрических цепей и уравнения акустических явлений, можно обнаружить некоторые аналогии.
Рассмотрим акустическую схему – простой акустический контур, представленный на рисунке 5.44.
На рисунке:
1- капиллярный канал;
2- полость объема V;
3- трубка с площадью сечения A;
u – скорость, p – давление.
Поскольку равенство давлений 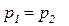 по разные стороны разграничивающих плоскостей означает равенство плотностей, из закона сохранения массы вытекает, что расход, вычисляемый как
по разные стороны разграничивающих плоскостей означает равенство плотностей, из закона сохранения массы вытекает, что расход, вычисляемый как
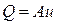 , (5.152)
, (5.152)
при переходе через эти плоскости сохраняется (т.е. течение сохраняется). Это течение можно рассматривать как аналог электрического тока, т.е. можно утверждать
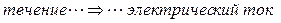 .
.
Аналогия акустической массы
Находящийся в трубе газ массой 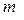 перемещается как целое под действием разности давлений
перемещается как целое под действием разности давлений 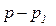 . Тогда справедливы соотношения
. Тогда справедливы соотношения
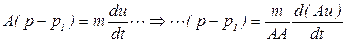 ,
,
откуда
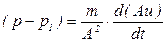 (5.153)
(5.153)
где 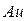 - расход газа.
- расход газа.
Приведем уравнение основного закона механики (динамики) имеет вид
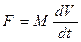 , (5.154)
, (5.154)
где 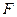 - сила, действующее на твердое тело с массой
- сила, действующее на твердое тело с массой 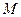 , под действием которой оно движется со скоростью
, под действием которой оно движется со скоростью 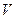 .
.
Также известно выражение для закона Ома
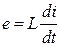 , (5.155)
, (5.155)
в котором 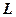 - индуктивность,
- индуктивность, 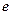 - разность потенциалов,
- разность потенциалов, 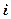 - ток.
- ток.
Как следует из рассмотрения полученных соотношений, уравнение для газа (5.153) близко по форме к уравнению механики (5.154) и выражению закона Ома. Формально сомножитель 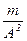 в правой части выражения (5.153) можно интерпретировать как акустическую массу.
в правой части выражения (5.153) можно интерпретировать как акустическую массу.
Таким образом, существует аналогия между механической массой 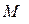 , индуктивностью
, индуктивностью 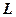 и акустической массой
и акустической массой 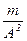 . При этом перемещение массы играет роль тока
. При этом перемещение массы играет роль тока
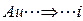 , (5.156)
, (5.156)
а разность давлений - разность потенциалов
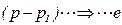 . (5.157)
. (5.157)
Акустическое сопротивление
Падение давления в капилляре, вызванное вязкостью, пропорционально скорости (при ламинарном течении).
Таким образом, получаем
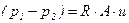 , (5.158)
, (5.158)
где 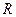 - аналог гидравлического сопротивления, которое называется акустическим сопротивлением.
- аналог гидравлического сопротивления, которое называется акустическим сопротивлением.
Акустическая упругость
Из-за малых размеров сжатие газа в полости происходит без смещения его центра массы. Процесс сжатия описывается законами термодинамики.
Предполагая сжатие адиабатическим (изменение количества теплоты, сообщенное в процессе, отсутствует, при котором можно принять 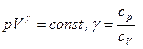 , где
, где 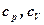 - удельная теплоемкость при постоянном давлении и объеме) получаем
- удельная теплоемкость при постоянном давлении и объеме) получаем
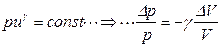 .
.  (5.159)
(5.159)
Справка.
Выражение  (5.159) можно получить из следующих выкладок.
(5.159) можно получить из следующих выкладок.
Введем обозначение 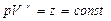
Из данного требования вытекает, что приращение переменной 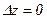 .
.
Найдем полный дифференциал 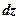 .
.
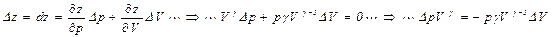 .
.
Отсюда имеем 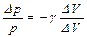 .
.
Пусть
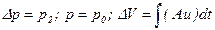 .
.
Тогда
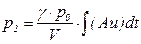 .
.  (5.160)
(5.160)
Сомножитель 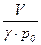 служит аналогом емкости в электричестве. Назовем его акустической емкостью.
служит аналогом емкости в электричестве. Назовем его акустической емкостью.
Уравнение акустического канала
Для представленной на рисунке схемы получим дифференциальное уравнение, связывающее давление 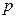 с потоком
с потоком 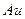 .
.
Имеем
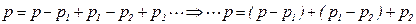 .
.
В правой части слагаемые заменим соответствующими выражениями из (5.153), (5.158), (5.160) и получим
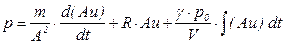 .
.  (5.161)
(5.161)
Полученное уравнение подобно закону Ома для последовательно включенных активного сопротивления 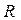 , индуктивности
, индуктивности 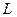 и емкости
и емкости 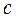
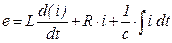 .
.  (5.162)
(5.162)
и механическому уравнению, описывающему затухающее движение тела с массой M с одной степенью свободы
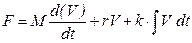 .
.  (5.163)
(5.163)
Сопоставление последних трех уравнений указывает на наличие аналогии с активными и реактивными сопротивлениями, соответствующие обозначения для которых приведено в таблице 5.5.
Таблица 5.5. Электро-механо-акустические аналоги
| Электрическая величина | Механическая величина | Акустическая величина | Графическое обозначение |
| Э.д.с., e | Механическая сила F | Акустическое давление, p | - |
| Ток, i | Линейная скорость, V | Объемный расход, Au | |
| Индуктивность, L | Масса, M | Акустическая масса, 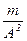
| |
Электрическое сопротивление, 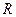
| Механическое сопротивление, 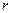
| Акустическое сопротивление, 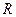
| |
| Емкость, c | Податливость (обратная величина жесткости), 1/k | Акустическая упругость, емкость,
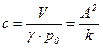
|
Эквивалентная схема микрофона
Все электроакустические системы можно разделить более или менее условно на три части:
- акустическую;
- механическую;
- электрическую.
Руководствуясь изложенными выше принципами, можно составить электрическую схему, эквивалентную исходной акустической.
При этом все элементы схемы, через которые проходит один и тот же поток, размещаются последовательно, а элементы, соответствующие частям общего потока, - параллельно.
Заметим, что в большинстве случаев сложение потоков проявляется в емкостях.
5.12.3.4. Микрофон, чувствительный к давлению
В микрофонах этого типа флуктуации давления 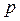 приводят к смещению диафрагмы. А изменение атмосферного давления не вызывает какого-либо эффекта (деформации) из-за наличия капиллярного канала для выравнивания давления.
приводят к смещению диафрагмы. А изменение атмосферного давления не вызывает какого-либо эффекта (деформации) из-за наличия капиллярного канала для выравнивания давления.
Подобные микрофоны содержат три элемента:
- полость;
- диафрагму;
- канал для подхода воздуха (капилляр),
которые можно представить соответственно с помощью емкости 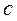 (ей соответствует импеданс Zс), импеданса реактивного типа ZD и активного сопротивления
(ей соответствует импеданс Zс), импеданса реактивного типа ZD и активного сопротивления 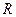 .
.
Получить выражение для определения давления, действующего на диафрагму.
Эквивалентная акустическая схема, построенная на основе аналогии с активным и реактивным сопротивлением, представлена на рисунке 5.45.
 Предположим, что давление, действующее на диафрагму и капилляр одинаковы. Далее выполняем расчет по эквивалентной электрической схеме (рисунок 5.45, в)).
Предположим, что давление, действующее на диафрагму и капилляр одинаковы. Далее выполняем расчет по эквивалентной электрической схеме (рисунок 5.45, в)).
Используем законы Кирхгофа.
Согласно первому закону (следствие закона сохранения зряда, согласно которому в любом узле заряд, одного знака не может ни накапливаться, ни убывать: алгебраическая сума токов ветвей, сходящихся в узле, равна нулю) имеем
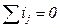 ;
;
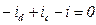 .
.
Согласно второму закону Кирхгофа (алгебраическая сумма напряжений всех участков замкнутого контура равна нулю; при составлении уравнений принято следующее правило: направление обхода участков контура – по часовой стрелке; со знаком плюс принять те слагаемые, в которых токи и э.д.с. имеют направление, совпадающее с направлением обхода) можно записать:
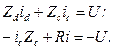 (5.164)
(5.164)
Решение системы (5.164) дает выражение
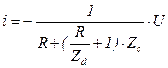 ,
,
в котором 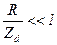 (активное сопротивление мало по сравнению с импедансом
(активное сопротивление мало по сравнению с импедансом 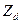 ). Откуда можно записать
). Откуда можно записать
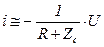 . (5.165)
. (5.165)
Учитывая, что 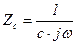 , из (5.165) получим
, из (5.165) получим
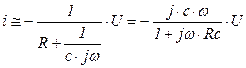 (5.166)
(5.166)
В полученном выражении тока 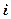 в соответствии с (5.156) является эквивалентом расхода газа (скорсти потока)
в соответствии с (5.156) является эквивалентом расхода газа (скорсти потока) 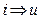 , а напряжение в соответствии с (5.157) – эквивалентом давления
, а напряжение в соответствии с (5.157) – эквивалентом давления 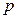
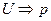 . Следовательно, выражение (5.166) можно переписать для искомых величин
. Следовательно, выражение (5.166) можно переписать для искомых величин 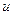
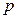
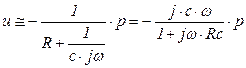 (5.167)
(5.167)
Определим силу, действующую на диафрагму.
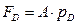 ,
,
где 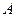 - площадь диафрагмы микрофона;
- площадь диафрагмы микрофона;
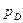 - давление на диафрагму.
- давление на диафрагму.
В соответствии со схемой (рисунок 5.25, б), в)) падение напряжения на импедансе 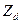 (давление на диафрагму) есть разница потенциалов на двух концах
(давление на диафрагму) есть разница потенциалов на двух концах 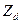 .
.
Это падение напряжения (давление) определяется по зависимости:
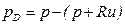 , (5.168)
, (5.168)
в которой первое слагаемое 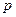 - есть давление на левом конце, а второе слагаемое - на правом конце импеданса
- есть давление на левом конце, а второе слагаемое - на правом конце импеданса 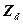 . Тогда сила будет равна
. Тогда сила будет равна
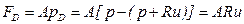 .
.
Последнее выражение с учетом (5.167) дает
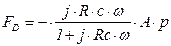 . (5.168)
. (5.168)
Значение 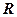 в (5.168) можно подобрать таким образом, чтобы всегда имело место
в (5.168) можно подобрать таким образом, чтобы всегда имело место 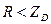 , а постоянная времени
, а постоянная времени 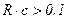 .
.
Этими параметрами определяется нижняя граница частот.
 5.12.3.5. Микрофон, чувствительный к градиенту давления
5.12.3.5. Микрофон, чувствительный к градиенту давления
Практически градиент можно определить, используя приближение: 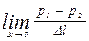 ,
,
где 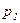 ,
, 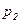 -давление в двух точках, расстояние между которыми
-давление в двух точках, расстояние между которыми 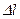 .
.
Пусть плоская волна направлена вдоль оси OX0, образуя угол 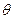 с осью OX (рисунок 5.46). Уравнение волны по давлению, направленному по оси OX0, согласно (5.142) имеет вид,
с осью OX (рисунок 5.46). Уравнение волны по давлению, направленному по оси OX0, согласно (5.142) имеет вид,
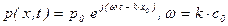 (5.169)
(5.169)
При 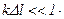 из (5.169) имеем
из (5.169) имеем
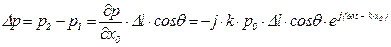 (5.170)
(5.170)
Сила, действующая на диафрагму площадью A, равна
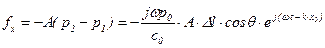 (5.171)
(5.171)
Для плоской волны имеет место
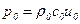 . (5.172)
. (5.172)
Подставив отсюда давление в (5.171) получим
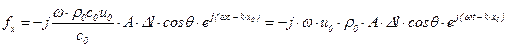 . (5.172)
. (5.172)
Из полученного выражения следует, что амплитуда силы, действующей на диафрагму, пропорциональна произведению линейной скорости на круговую частоту.
Этот вывод не зависит от формы волны. В самом деле, основное уравнение динамики имеет вид (что следует из закона сохранения количества движения, см. (5.143))
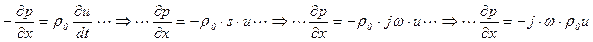 .
.
Отсюда следует
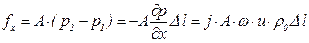 . (5.173)
. (5.173)
Напротив, чувствительность к давлению 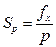 зависит от формы волны.
зависит от формы волны.
Для плоской волны с углом падения 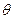 имеем
имеем
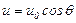 и
и 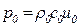 .
.
Используя выражения (5.172) и (5.169), получим
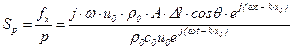 ,
,
откуда вытекает
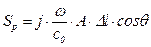 . (5.174)
. (5.174)
Для сферической волны радиусом 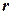 и с центом на оси OX0, удовлетворяющей условию
и с центом на оси OX0, удовлетворяющей условию
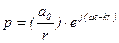 ,
,
имеем
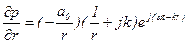 .
.
С учетом очевидных соотношений
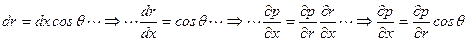
получим
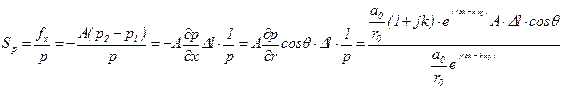 .
.
 Отсюда имеем
Отсюда имеем
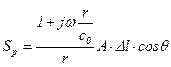 . (5.175)
. (5.175)
Из сравнения выражений (5.174) и (5.175) очевидно, что чувствительность к давлению 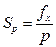 действительно зависит от формы волны.
действительно зависит от формы волны.
5.12.3.6. Микрофоны смешанного типа (чувствительные как к давлению, так и к градиенту давления)
 Рассмотрим микрофон (рисунок 5.47), полость которого закрыта, а на противоположной стороне имеется окно, регулируемое акустическим сопротивлением (на рисунке: 1 – полость; 2 – сопротивление; 3 – механическая связь с преобразователем; 4 – диафрагма).
Рассмотрим микрофон (рисунок 5.47), полость которого закрыта, а на противоположной стороне имеется окно, регулируемое акустическим сопротивлением (на рисунке: 1 – полость; 2 – сопротивление; 3 – механическая связь с преобразователем; 4 – диафрагма).
Эквивалентная расчетная электрическая схема микрофона представлена ниже на рисунке 5.48.
Вследствие существованния зазора Δl между двумя поверхностями давления p1иp2, приложенные к этим поверхностям, различаются.
Для случая плоской волны, образующей с осью микрофона угол θ, получим
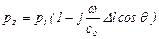 ;
;
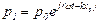 ;
;
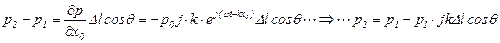 .
.
Отсюда
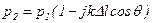 . (5.176)
. (5.176)
Отметим, что акустическое сопаротивление R значительно меньше, чем в случае, рассмотренном выше, поскольку относится к окну, а не к капиллярному отверстию.
Используя акустическую аналогию, можно записать (что следует из законов Кирхгофа)
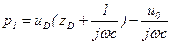 , (5.177)
, (5.177)
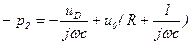 . (5.178)
. (5.178)
Очевидно, что даление на диафрагму 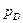 есть разность потенциалов на двух концах
есть разность потенциалов на двух концах 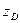 .
.
Отсюда имеем:
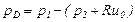 .
.
Выражение для давления 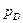 получим их трех последних уравнениий (5.176) - (5.178)
получим их трех последних уравнениий (5.176) - (5.178)
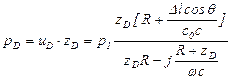 ,
,
откуда следует выражение для силы 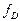 , действующей на диафрагму:
, действующей на диафрагму:
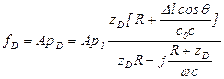 . (5.179)
. (5.179)
При условии 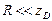 имеем
имеем
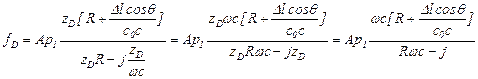 .
.
Умножая числитель и знаменатель последнего выражения на 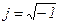 , получим
, получим
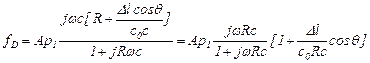 .
.
Вводя обозначение 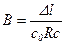 , из последнего уравнения получим
, из последнего уравнения получим
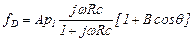 . (5.180)
. (5.180)
Полученное выражеие для общего слусая.
Частный случай, когда можно принять 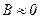 , соответствует микрофону, чувствительному к давлению (см. разд. 5.12.3.4, соотношение(5.168)).
, соответствует микрофону, чувствительному к давлению (см. разд. 5.12.3.4, соотношение(5.168)).
При 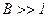 имеем микрофон, чувствительный к градиенту.
имеем микрофон, чувствительный к градиенту.
Пример.
Пусть 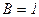 ,
, 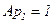 .
.
Используя зависимость (5.180), получим линии постоянных давлений (диаграмму направленности) микрофона.
 Для этого находим модуль давления
Для этого находим модуль давления 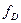 , определяемого по соотношению (5.180), из выражения
, определяемого по соотношению (5.180), из выражения
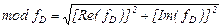
На рисунке 5.49 приведены такие линии для двух значений 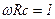 и
и 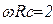 .
.
5.12.4. Измерение интенсивности
5.12.4.1. Принцип измерения интенсивности звука
Интенсивность звука определяется как осредненное по времени произведение звукового давления на его скорость.
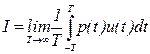 . (5.181)
. (5.181)
Поскольку скорость звука непосредственно измерить сложно, то для связывания скорости и градиента давления используется уравнение динамики
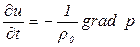 , (5.182)
, (5.182)
где 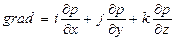 .
.
Выражение для интенсивности с учетом (5.181) и (5.182) вдоль направления оси OX примет вид
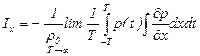 . (5.183)
. (5.183)
При практических измерениях используют пару микрофонов, расположенных достаточно близко друг к другу, чтобы получить хорошую оценку градиента давления по конечной разности:
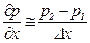 ;
; 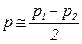 .
.
Дата добавления: 2021-12-14; просмотров: 782;











