Различают автоматы синхронные и асинхронные.
В синхронном автомате переходы приурочены к определенным моментам времени, задаваемым сигналами от внешнего источника. В промежутках времени между этими сигналами входные буквы могут меняться, но это не влечет немедленных изменений состояния и выхода.
В асинхронном автомате переходы приурочены к моменту изменения входных переменных. Пока входная буква не меняется, переход не происходит. Поэтому говорят, что у асинхронного автомата все состояния устойчивы: однажды возникнув под действием входной буквы хi они сохраняются как угодно долго, если эта буква не меняется.
Напротив, в синхронном автомате некоторые состояния могут быть неустойчивыми: при сохранении неизменной входной буквы переходы могут происходить неоднократно, с поступлением очередных синхросигналов.
Заметим, что если сигнал синхронизации считать просто одной из компонент структурного входного вектора и соответственно расширить (вдвое) входной абстрактный алфавит, то любой работоспособный автомат окажется асинхронным.
Таким образом, разделение автоматов на синхронные и асинхронные имеет искусственный характер, но оно практически оправдано. Оно упрощает структурные аспекты реализации автомата, а в абстрактной теории исключение сигнала синхронизации из числа структурных входных переменных вдвое уменьшает число букв в абстрактном входном алфавите.
В абстрактной теории бессмысленно говорить об "одновременности" или "неодновременности" тех или иных процессов внутри одного интервала автоматного времени, поэтому единственным признаком синхронности или асинхронности автомата является устойчивость или неустойчивость его состояний. Автомат является синхронным, если хотя бы одно его состояние неустойчиво (рис. 2.5).
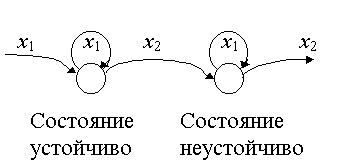
Рис. 2.5
С - автоматом называют ЦА, сочетающий свойства автоматов Мили и Мура, причем свойство вырабатывать выходной сигнал соответственно той или другой модели различно для разных переходов. Например, можно представить себе счетчик, который выдает значения накопленной суммы как автомат Мура, а сигнал переполнения выдает только в момент обнуления.
Модель С-автомата часто рассматривается в специальной учебной литературе, но не представляет ни практического, ни заметного теоретического интереса, так как легко может быть заменена одной из основных моделей.
Автономным автоматом называется особый ЦА, у которого отсутствует вход. Он работает независимо от внешней среды по своей внутренней программе. Очевидно, он является автоматом Мура с предельно простыми функциями. Пример такого автомата показан на рис. 2.6.
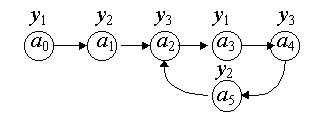
Рис. 2.6
Этот автомат генерирует единственное бесконечное слово с циклически повторяющимся сегментом:
Sy = y1y2y3(y1y3y2y3)
При отсутствии цикла автомат должен будет в предопределенный момент остановиться в некотором конечном состоянии.
Если допустить, что внешнее воздействие может в любой момент прерывать цепочку переходов и возвращать автомат в начальное состояние, то тогда автомат сможет генерировать множество различных слов, но всегда любое короткое слово будет представлять начальный отрезок более длинного слова.
Автономный автомат не представляет самостоятельного интереса, так как если внешнее воздействие, возвращающее его в начальное состояние, включить в состав структурного входного вектора и соответствующим образом восстановить входной абстрактный алфавит, то он превратится в обычный автомат Мура.
Рассмотрим абстрактный автомат как преобразователь информации. Для удобства рассуждений возьмем простой автомат Мура, заданный графом (рис.2.7).
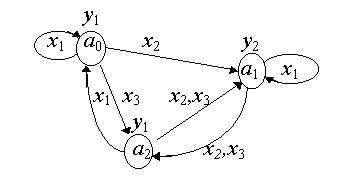
Рис. 2.7
Зададимся входным словом Sx и прослеживая по рисунку изменения внутренних состояний и выходных букв, составим последовательность:
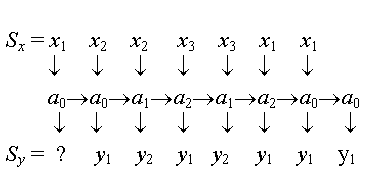
Рассматривая выходное слово автомата Мура как его реакцию на слово входное, не следует включать в него первую букву, существовавшую на выходе в момент t =0. Эта буква в приведенной здесь последовательности заменена вопросительным знаком. Практически выходной сигнал автомата Мура при t = 0 задают как пустую букву е.
Для автомата Мили этой проблемы нет, так как до появления первой буквы входного слова он не выдает информации.
В рассмотренном примере автомат выполнил одно из возможных для него преобразований Sx® Sy. При другом входном слове получилась бы другая последовательность состояний и другое выходное слово, но некоторый общий закон преобразования входных слов в выходные непременно сохранился бы.
Общий закон, определяемый функциями d и l , можно рассматривать как соответствие из бесконечного множества входных слов во множество слов выходных. Это соответствие называется алфавитным оператором F
Sу = F(Sx).
Понятие алфавитного оператора можно использовать в более широком смысле, чем описание функции некоторого цифрового автомата. Алфавитный оператор представляет более высокую степень абстракции. Здесь уже исчезает разница между автоматом и алгоритмом, появляется возможность рассматривать вопросы, не сводящиеся к анализу или синтезу автоматов. Они интересуют современную математику в связи с общей проблемой алгоритмической разрешимости её задач. Если автомат не является частичным, то вместо слов "алфавитный оператор" можно использовать более узкий термин "автоматное отображение".
В абстрактной теории важен и другой взгляд на ЦА, уже не как на преобразователь информации, а как на её распознаватель.
Допустим, что выходной алфавит некоторого автомата состоит из двух букв
Y = {y1, y2}.
Всё множество входных слов разобьем на два класса: в первый класс отберем слова, которые будучи переработаны в выходные, оканчиваются на у1, а во второй - все остальные слова. При этих условиях автомат становится распознавателем входных слов. Текущее значение выхода является ответом на вопрос: относится или нет принятое к этому моменту слово к определенному классу. Выходные слова становятся просто последовательностями ответов на вопрос, какому классу принадлежит последнее принятое слово.
При сравнении автоматов можно обнаружить такие их отношения, как гомоморфизм, изоморфизм и эквивалентность
Изоморфными являются автоматы, у которых совпадают модели (Мили или Мура), совпадает число букв в соответственных алфавитах, а функции переходов и выходов настолько одинаковы, что можно сделать автоматы неотличимыми путем переименования букв в алфавитах. В абстрактной теории изоморфные автоматы можно считать просто одинаковыми, но на структурном уровне они могут заметно отличаться и быть неравноценными по быстродействию и объему оборудования.
Односторонний гомоморфизм автоматов возможен, когда у одного из них область определения автоматных функций d и l шире и перекрывает область определения второго. Тогда первый является гомоморфным по отношению к второму, но не наоборот. Легче всего можно представить такую ситуацию, если считать, что сравниваемые автоматы имеют одинаковые соответственные алфавиты, но по крайней мере один из них является частичным. Совпадающие результаты такие автоматы будут давать только в том случае, если входные слова не окажутся запрещенными для одного из них.
Эквивалентными сравниваемые автоматы являются в том случае, если они одинаковым образом преобразуют входные слова в выходные. При этом необходимо, чтобы автоматы имели одни и те же входной и выходной алфавиты, но совершенно необязательно, чтобы у них было одинаковое число состояний. Не имеет значения даже модель (Мили или Мура).
Используя понятие алфавитного оператора можно дать наиболее точное и краткое определение свойства эквивалентности: эквивалентные автоматы имеют одинаковые алфавитные операторы.
Синтез автомата по схеме алгоритма
Синтез автомата Мили начинается с установления связи между определенными этапами выполнения заданного алгоритма и состояниями автомата. Автомат Мили сперва выдает выходную букву, а затем изменяет свое состояние. Обе его функции: переходов и выходов зависят от пары "состояние-вход" в момент t:
y(t) = l (a(t), x(t));
a(t+1) = d (a(t), x(t)).
Из определения вытекает, что каждый раз после выдачи очередной буквы "у" автомат оказывается в очередном состоянии "а". Нужно найти на схеме алгоритма соответствующие точки, отметить их (например, крестиками) и пронумеровать.
Пример 1. На рис. 7.1 показан подграф некоторой схемы алгоритма. Крестиками отмечены входы вершин графа, находящихся сразу за операторами. Крестики должны находиться не у выходов операторных вершин, а именно у входов следующих вершин после всех возможных слияний путей графа. В противном случае число намечаемых состояний неоправданно увеличится.
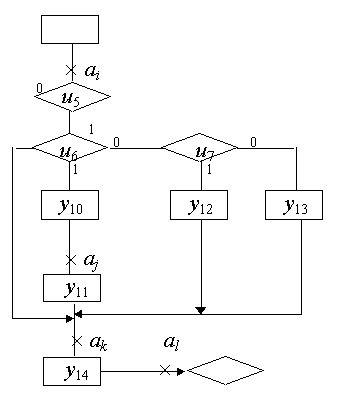
Рис. 7.1
Определим переходы автомата из состояния аi в аk. Для этого исследуем все пути на графе, ведущие от отметки аi к отметке аj. Из них нас должны интересовать только пути, содержащие одну операторную вершину графа. Путь через u5 не содержит операторных вершин и в данный момент не представляет интереса. Он понадобится впоследствии, когда будут просматриваться пути от аi к аl. Путь через u5u6y10y11 содержит две операторные вершины и должен соответствовать не одному, а двум переходам автомата.
Остаются два пути, отвечающие поставленному требованию: u5u6u7y12 и u5u6u7y13. Заключаем, что из аi в аk должно быть определено два перехода: при ЛУ u5u6u7 с выдачей у12 и при ЛУ u5u6u7 с выдачей у13. Соответствующий подграф графа переходов автомата Мили показан на рис. 7.2.
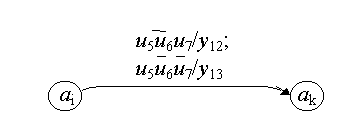
Рис. 7.2
Пример 2. Здесь пара вершин соединена несколькими путями, проходящими через одну и ту же операторную вершину, но при разных ЛУ (рис. 7.3).
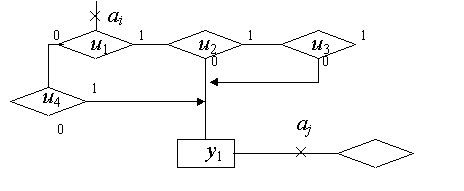
Рис. 7.3
Логические условия такого перехода можно было бы описать дизъюнкцией
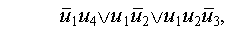
но практически такую запись не используют. Если полученное дизъюнктивное выражение поддается упрощению до элементарной конъюнкции, то это упрощение должно быть проделано, и соответствующая часть схемы алгоритма должна быть исправлена. Если же формула не упрощается, то для каждого пути алгоритма определяется отдельный переход. Обозначения отдельных переходов над дугами графа автомата разделяются запятыми. Такое разделение всё равно пришлось бы сделать впоследствии, при структурном синтезе.
Рассуждения, подобные изложенным в примерах 1 и 2, повторяются для каждой пары отметок состояний. Учитываются также замкнутые пути (петли), даже если они не содержат оператора. Такие пустые петли соответствуют режиму ожидания. Если путь приводит в конец алгоритма, то он тоже учитывается, даже если не содержит оператора. Такие пути, как и петли без оператора, отмечаются пустым оператором "е".
Перед началом работы автомат должен находиться в начальном состоянии и в это же состояние должен вернуться по окончании выполнения алгоритма. Поэтому отметка а0 делается как у входа вершины СА, идущей непосредственно после начальной, так и у входа в конечную вершину.
Пример 3. Зададимся СА на рис.7.4 и следуя описанной методике построим граф автомата Мили (рис.7.5).
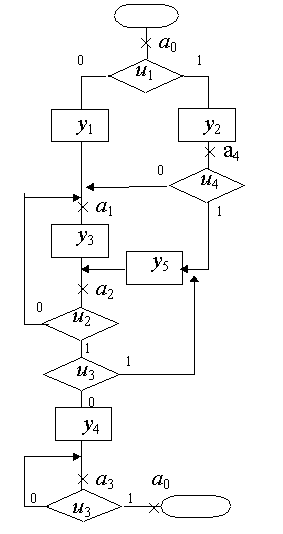
Рис. 7. 4
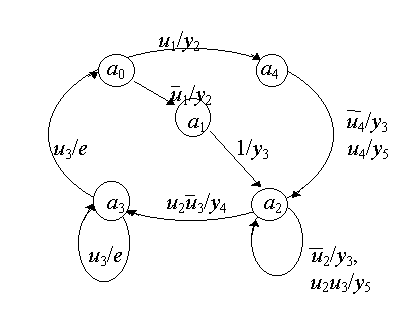
Рис. 7.5
Прежде всего, расставим отметки состояний на СА. Понадобилось шесть отметок, из которых две одинаковых - а0. Затем двигаемся по СА от отметки до отметки, прослеживая все пути согласно описанным правилам.
Как уже говорилось, синтез по СА ведется с использованием структурного алфавита U. Если почему-либо требуется перейти к абстрактному входному алфавиту Х, то ввиду наличия в данном примере четырех структурных переменных u1...u4 число абстрактных букв "х" должно составить 24 = 16. Обычная таблица переходов и выходов имела бы 16 столбцов. Строк же было бы столько же, сколько состояний, т.е. пять.
Структурное представление входного алфавита позволяет применить вместо громоздкой таблицы переходов и выходов список автомата, т.е. таблицу, в которой строка за строкой перечисляются все имеющиеся в автомате переходы. Для рассмотренного примера список автомата дан в табл. 7.1
Таблица 7.1
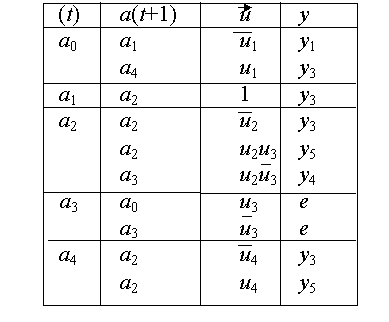
Список удобнее обычной таблицы переходов, так как имеет постоянную ширину и гораздо компактнее. Особенно сильно упрощается здесь запись безусловных переходов.
Синтез автомата Мура по СА выполняется в основном аналогично описанному. Отличия вызваны свойствами функции выходов, которая здесь определяется только состоянием автомата
y(t) = l (a(t)).
Поэтому отметки состояний делаются не в виде крестиков на линиях связи, а непосредственно у операторных вершин СА. Отметка начального состояния а0 ставится у начального и конечного терминаторов алгоритма.
Названное отличие приводит к необходимости корректировать СА, устраняя детали, не поддающиеся реализации в автомате Мура.
Режим ожидания не может быть представлен петлей у проверки логического условия. Необходимо включить в такую петлю пустой оператор "е" или превратить ждущую вершину графа в возвратную вершину (рис. 7.6).
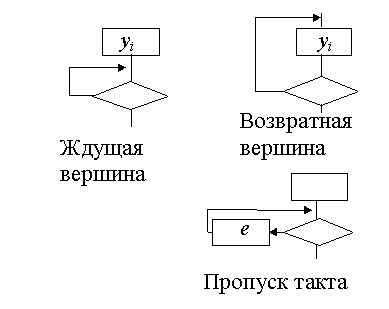
Рис. 7.6
Возвратная вершина выгоднее, чем пропуск такта, так как не добавляет новых состояний, но она может быть организована только тогда, когда содержание оператора уi допускает его повторение (например, можно повторять команду сброса регистра, команду пересылки, но не сдвига или сложения). Если ждущая вершина СА находится в начале алгоритма, то проще всего режим ожидания можно организовать соединив выход этой вершины с конечным терминатором.
Во всех случаях, когда СА содержит петли с двумя или несколькими проверками логических условий (при синтезе любой модели автомата), нужно обратить внимание на правильное замыкание этих петель. Дело в том, что проверки логических условий одного перехода выполняются одновременно, и СА должна соответствовать этому требованию (рис. 7.7).
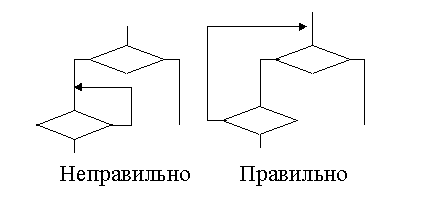
Рис. 7.7
Пример 4. По той же СА синтезируем автомат Мура. Разметка состояний показана на рис. 7.8.
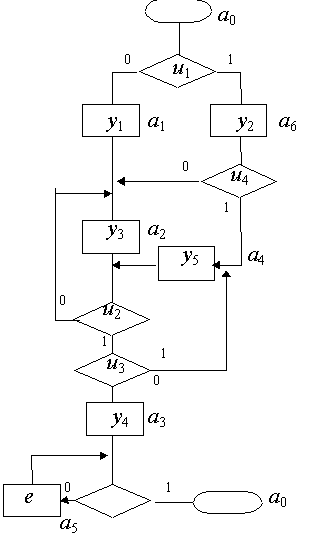
Рис. 7.8
Число состояний автомата Мура оказалось равным семи, т.е. увеличилось на два по сравнению с автоматом Мили. Граф автомата строим как в примере 3, но обозначения выходных букв надписываем не над дугами, а над вершинами. Граф автомата Мура показан на рис. 7.9.
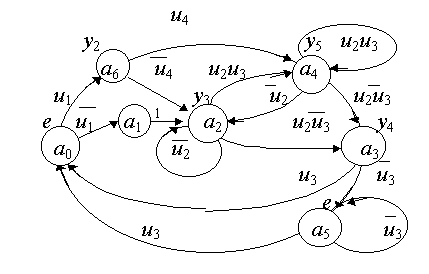
Рис. 7.9
Список автомата Мура (табл.7.2) имеет только три столбца, так как выходные буквы можно записать вместе с состояниями a(t). Составлением списка с абстрактными обозначениями состояний абстрактный синтез заканчивается, так как следующая задача - кодирование состояний относится к уровню структурного синтеза.
Таблица 7.2

Позиционные системы счисления
Позиционная запись числа A подразумевает его представление в виде суммы
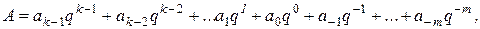
где 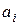 -цифры от 0 до q -1, q -основание системы счисления, k -число разрядов в целой части числа, m -то же в дробной части. В дальнейшем мы всюду будем пользоваться обозначением общего числа разрядов:
-цифры от 0 до q -1, q -основание системы счисления, k -число разрядов в целой части числа, m -то же в дробной части. В дальнейшем мы всюду будем пользоваться обозначением общего числа разрядов:
n=k+m
Фактически число записывается как ряд цифр, а для указания начала отсчета степеней основания системы служит q-ичная запятая или “точка”.
Общие принципы арифметики в любой из позиционных систем одинаковы. Различия сводятся к неодинаковому количеству используемых цифр. Чем больше допустимых цифр, тем больше получается парных сочетаний этих цифр в элементарных операциях. В десятичной арифметике таблицы элементарных операций сложения или умножения имеют размер 10х10 = 100, а в шестнадцатеричной - 16х16 = 256.
Самые простые правила у двоичной арифметики. Таблицы сложения и умножения имеют размер 2х2, причем функция суммы двух цифр совпадает с логической функцией неравнозначности, а функции переноса и произведения одинаковы и совпадают с конъюнкцией. В результате действия над многоразрядными числами тоже оказываются очень простыми. Примеры:
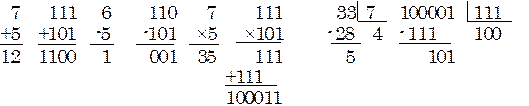
Особенно заметное упрощение получается при умножении и делении чисел. Умножение превращается в ряд сдвигов и сложений, а при делении не приходится подбирать очередную цифру частного - вычитание то происходит, то не происходит.
Простота правил арифметики, сводимость элементарных операций к функциям булевой алгебры и, наконец, легкость технической реализации двоичных сигналов и записи двоичных кодов на любых носителях информации - вот причины исключительного применения двоичной системы в современных ЭВМ.
При q > 2 действия намного усложняются. При выполнении операций “вручную” каждое элементарное действие приходится разбивать на два шага. Складывая две цифры, мы сперва в уме находим сумму по правилам десятичной арифметики, затем переводим её в систему счисления с заданным основанием и только после этого делаем соответствующую запись. Аналогично действуем при умножении. Сперва две цифры перемножаются в уме в десятичной системе, затем к результату (в уме) прибавляется перенос. Только после этого результат перемножения двух цифр переводится в нужную систему.
Примеры:
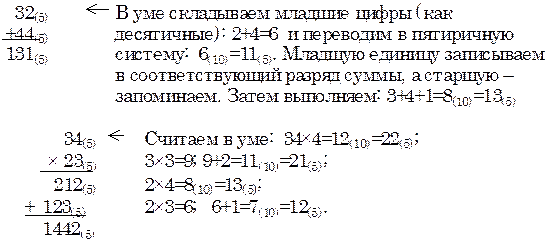
Из систем с основанием, отличным от 2, основной интерес представляют две системы: десятичная и шестнадцатеричная. Первая из них необходима, по крайней мере, для ввода и вывода чисел, а вторая, как и другие системы с основанием, кратным целой степени двойки, обладает определенными преимуществами перед другими системами. По сравнению с двоичной системой запись числа в шестнадцатеричной системе гораздо компактнее, так как одна шестнадцатеричная цифра заменяет тетраду двоичных цифр:
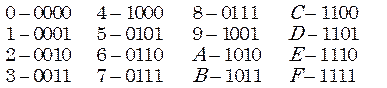
Шестнадцатеричная система не создает никаких проблем для машинной арифметики, так как при сложении и вычитании сохраняются правила двоичной арифметики. Фактически в сложении участвуют двоичные эквиваленты шестнадцатеричных чисел. Пример:
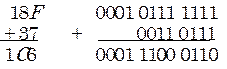
Десятичные числа в машине тоже заменяются двоичными тетрадами, но правила арифметики получаются гораздо более сложными. Они будут рассмотрены позже, а сейчас перейдем к вопросу о переводе чисел из одной системы счисления в другую.
Проще всего этот вопрос решается, если у обеих систем: “старой” и “новой” основание равно целой степени двойки. При этом для перевода чисел достаточно в качестве промежуточной формы записать двоичный эквивалент, а затем перегруппировать разряды по-новому, начиная от запятой вправо и влево. Переведем восьмеричное число 35,3 в шестнадцатеричную систему:

Описанное преобразование является частным случаем. В более общем случае перевод выполняется с помощью специального вычисления. Из определения позиционного числа вытекает формула для преобразования целых чисел из системы с основанием p в систему с основанием q:

Этой формуле соответствует следующий алгоритм преобразования (все действия выполняются по правилам q – ичной арифметики):
1) умножить старшую цифру исходного числа на старое основание p, выраженное в новой системе q,
2) прибавить к предыдущему результату следующую цифру числа,
3) повторить пункт 2,
4 повторять п.п. 3 и 4 до исчерпания разрядов числа.
Для правильных дробей аналогичное по смыслу преобразование задает формула:
 .
.
Соответствующий алгоритм в словесном описании:
1) разделить младшую цифру исходного числа на p,
2) прибавить к предыдущему результату следующую цифру числа,
3) разделить предыдущий результат на p,
4) повторять п.п. 2 и 3 до исчерпания разрядов числа. Заметим, что выполнение указанных действий неизбежно связано с округлением результата. Все действия описанных алгоритмов выполняются по правилам арифметики с «новым» основанием.
Существуют также алгоритмы, противоположные описанным. Для целых чисел:
1) разделить A(p) на q(p). Деление выполняется по правилам «старой» арифметики с основанием p. Остаток от деления запомнить, - это будет младшая цифра искомого числа,
2) предыдущее частное снова разделить на q и запомнить остаток,
3) повторять п. 2, пока не получится частное, меньшее, чем q. Число A(q) представится рядом остатков, записанных в порядке, обратном их получению, а старшей цифрой будет последнее частное.
Переведем по этому алгоритму десятичное число 106 в троичную систему: 
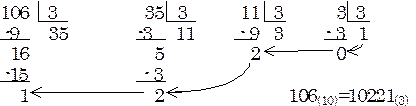
Для правильных дробей этот вариант алгоритма будет формулироваться следующим образом:
1) умножить дробь A(p) на q(p) по правилам «старой» арифметики. Целую часть произведения запомнить. Это будет старшая цифра искомой дроби,
2) дробную часть предыдущего произведения вновь умножить на q и запомнить целую часть произведения,
3) повторять п. 2, пока не будет получено нужное число разрядов новой дроби A(q). Она запишется как ряд целых частей произведений, записанных в порядке их получения.
Переведем по этому способу в десятичную систему двоичную дробь 0,00111101 с точностью до двух значащих цифр:
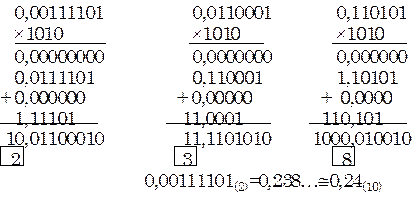
Если число является смешанной дробью, то при любом варианте алгоритма его нужно переводить по частям: целую и дробную части по отдельности с последующим объединением результатов.
Кодирование отрицательных чисел (Лекция 19)
Числа с фиксированной точкой и мантиссы чисел с плавающей точкой могут участвовать в машинной арифметике в одном из трех кодов: прямом, дополнительном или обратном. Дадим определения этих кодов для целых двоичных чисел. Общее число разрядов, включая знаковый, будем обозначать буквой n. Нумерация, согласно общепринятому правилу, начинается с нуля. Таким образом, разряд с весом 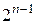 будет являться знаковым. Для упрощения записей будем пользоваться следующими обозначениями:
будет являться знаковым. Для упрощения записей будем пользоваться следующими обозначениями:
|A| -модуль числа A;
áAñ - прямой код того же числа;
ááAññ - дополнительный код того же числа;
áááAñññ - обратный код того же числа.
Прямым кодом числа А называется запись
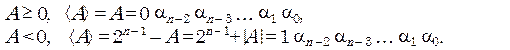
Прямой код совпадает с записью числа в определенной нами ранее естественной форме. Число - 1010 в прямом коде запишется как 11010. В этом коде нуль имеет два значения: + 0 = 0000.....0 и - 0 = 1000.....0.
В этом коде можно складывать числа, имеющие одинаковые знаки. При этом знаковые цифры не складываются, как все остальные, знак суммы определяется отдельной логической операцией. Переносы в знаковый разряд не допускаются. Примеры сложения чисел в прямом коде:

Выделенные нами знаковые цифры результата получаются логически, т.е. результату присваивается тот же знак, что у слагаемых. Сложение знаковых цифр недопустимо, так как оно ведет к неправильному результату. Во втором примере получилось бы 1+1=10, единица переноса была бы потеряна, а в знаковом разряде остался бы нуль.
При вычитании или, что то же самое, при сложении чисел с противоположными знаками пришлось бы реализовать очень сложный алгоритм. Сперва каким-то путем устанавливать, какое из слагаемых имеет больший модуль (например, с помощью специальной комбинационной логической схемы) и запоминать его знак, затем из большего модуля вычитать меньший. Практически это никогда не делается, просто прямой код не используется для алгебраического сложения, то есть для сложения чисел с произвольными знаками.
Дополнительным кодомназывается запись:
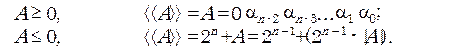
Член вне скобок - это единица знакового разряда, а внутри скобок находится дополнение модуля числа A до 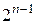 . Сравним графические представления чисел в прямом и дополнительном кодах (рис. 3.1).
. Сравним графические представления чисел в прямом и дополнительном кодах (рис. 3.1).

Рис. 3.1
Стрелки указывают направление увеличения модуля, скобки определяют, каким сегментам принадлежат граничные точки. Из рисунка видно, что в дополнительном коде, как и в прямом, для изображения отрицательных чисел выделен отрезок положительной числовой оси. Отличие состоит в том, что в дополнительном коде отсчет на этом отрезке идет справа налево.
Дополнение модуля числа до 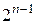 теоретически определяется вычитанием. Например: n = 6; А = - 00101. Вычтем модуль A из
теоретически определяется вычитанием. Например: n = 6; А = - 00101. Вычтем модуль A из 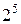
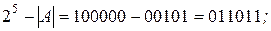

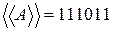
Находить дополнение вычитанием в машинной арифметике нельзя, так как вычитание в обычном смысле этого слова вообще не используется. Машинный алгоритм основан на преобразовании:
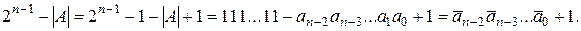
Поразрядное вычитание двоичных цифр из единицы равносильно их инвертированию как логических переменных, что выполняется очень просто. Чтобы преобразовать прямой код отрицательного числа в дополнительный, нужно, не меняя знаковой цифры, проинвертировать цифры модуля и прибавить единицу. Для обратного перехода, казалось бы, требуются противоположные действия, т.е. сперва отнять единицу, а потом проинвертировать цифры дополнения. Однако точно такой же результат получается при повторном применении прямых действий: инверсия и плюс единица. Дело в том, что вычитать единицу из дополнения или прибавлять единицу к модулю - это равносильные операции.
В дополнительном коде нуль имеет только одно значение: «плюс нуль». Попытаемся получить «минус нуль»
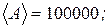
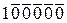 +1 = 111111+1 =
+1 = 111111+1 = 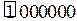
Выделенная рамочкой единица выходит из разрядной сетки и теряется. В пределах принятого формата числа остается код «плюс нуля».
 В дополнительном коде сложение и вычитание выполняются одинаково, как алгебраическое сложение чисел с произвольными знаками. При этом знак суммы получается арифметическим путем, благодаря распространению сложений и переносов на знаковый разряд. Рассмотрим сложение при разных сочетаниях знаков слагаемых В, С и суммы А.
В дополнительном коде сложение и вычитание выполняются одинаково, как алгебраическое сложение чисел с произвольными знаками. При этом знак суммы получается арифметическим путем, благодаря распространению сложений и переносов на знаковый разряд. Рассмотрим сложение при разных сочетаниях знаков слагаемых В, С и суммы А.
1) В > 0, С > 0. Этот вариант выполняется как в обычной арифметике и внешне - как в прямом коде, но знак суммы определяется сложением
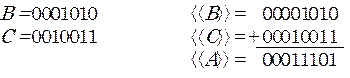
2) В > 0, C < 0, |A| > |C|. Этот вариант равносилен вычитанию положительного С :
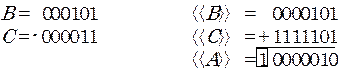
Заключенная в рамку единица переноса из старшего разряда суммы теряется. Ее потеря не является ошибкой. Дополнительный код отрицательного числа по определению отличается от истинной величины числа на константу, равную 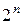 . При получении положительной суммы эта константа оказывается лишней и должна исчезнуть;
. При получении положительной суммы эта константа оказывается лишней и должна исчезнуть;
3) В > 0, C < 0, |B| < |C|.
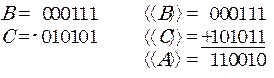
4) В < 0, C < 0. В этом варианте для формирования кода отрицательного числа требуется одна константа 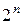 , а поступают со слагаемыми -две. Одна из них должна исчезнуть.
, а поступают со слагаемыми -две. Одна из них должна исчезнуть.
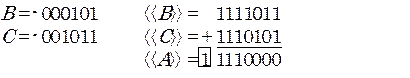
Обратным кодом называется запись:

Обратный код отличается от дополнительного отсутствием единицы, прибавляемой после инвертирования. Эту отсутствующую единицу иногда приходится прибавлять искусственно, чтобы скорректировать результат сложения. В обратном коде нуль имеет два значения: «плюс нуль» 0000....0 и «минус нуль» 1111...1. Сложим в обратном коде числа с разными сочетаниями знаков:
1) В > 0, C > 0. Этот случай в любом коде выполняется одинаково.
2) В > 0, C < 0, |B| > |C|.
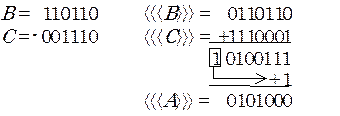
Объясним причину необходимости так называемого «циклического переноса». В коде отрицательного слагаемого недоставало единицы младшего разряда (по определению кода). Сумма получилась положительной, а здесь по определению прямого кода недостача единицы не предусмотрена. Следовательно, эту единицу следует прибавить искусственно. Признаком данной ситуации является перенос из старшего разряда суммы, который уносит константу, входившую в код отрицательного слагаемого. «Циклический перенос», это - всего лишь мнемонический прием, означающий, что если при сложении обратных кодов произошел перенос из знакового разряда, то необходимо скорректировать сумму.
3) В > 0, C < 0, |B| < |C|.
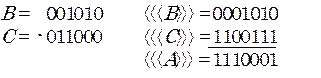
4) B < 0, C < 0.
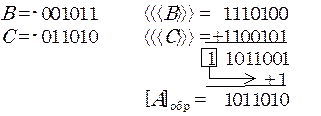
Правильные двоичные дроби в прямом, дополнительном и обратном кодах изображаются подобно целым числам, но в определении кодов используются другие константы:
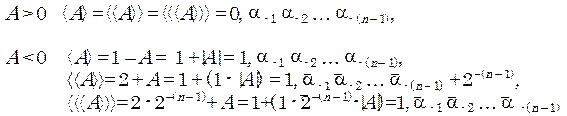
В заключение этой темы запишем определения прямого, дополнительного и обратного кодов для целых чисел при произвольном основании системы счисления q.
.
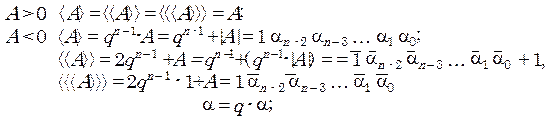
Обратим внимание на то, что здесь при формировании дополнительного и обратного кодов инвертирование цифр определяется как арифметическое дополнение до старшей цифры в данной системе.
Для правильных дробей определения прямого, дополнительного и обратного кодов описываются следующими выражениями:
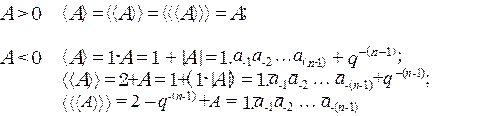
Сложение и умножение двоичных чисел
Сложение
В дальнейшем при описании алгоритмов выполнения арифметических операций в процессоре мы будем пользоваться языком функционального микропрограммирования или "Ф-языком". Примеры выражений этого языка:
С :=R 2(С) -логический сдвиг на два разряда вправо в регистре С,
В :=В[n-1].L1(B).0 -арифметический сдвиг дополнительного кода в регистре В на один разряд влево,
А :=С -пересылка числа из регистра С в регистр А,
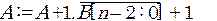 -вычитание из числа А модуля числа В с использованием дополнительного кода.
-вычитание из числа А модуля числа В с использованием дополнительного кода.
Язык функционального микропрограммирования очень прост и гибок, позволяет с помощью оператора присваивания записывать любые элементарные действия над числами. Сами числа своих наименований не имеют, под числом подразумевается содержимое определенного регистра.
Ниже мы будем придерживаться следующих обозначений регистров или регистровых пар: В и С - регистры - источники, А - аккумулятор, т.е. регистр, непосредственно связанный с выходом сумматора. Результат операции обычно помещается на место первого операнда, но это происходит лишь в конце операции, поэтому ради простоты описания алгоритмов эту заключительную пересылку мы не будем учитывать.
Рассмотрим сложение A := В + С. Допустим, что числа загружаются в процессор и выгружаются из него в дополнительном коде. Алгебраическое сложение чисел при этом происходит проще, чем при использовании прямого кода. Существуют два варианта организации сложения: одноадресный и двухадресный.
При одноадресном способе на одно и то же "плечо" сумматора сперва подается первое слагаемое В, а затем второе С. Результат помещаются в аккумулятор А (рис. 5.1).

Рис. 5.2 показывает микропрограмму одноадресного сложения. Признак переполнения f здесь получается сложением по модулю 2 двух величин переноса: в знаковый разряд и из него. Логический способ контроля переноса путем сопоставления знаков операндов и знака результата здесь невозможен, так как знаковые цифры слагаемых не могут быть прочитаны одновременно.
На рис. 5.1 и 5.2, как и в дальнейшем, применены обычные обозначения признаков результата (флагов) и логических переменных. OF – флаг переполнения, CF – флаг переноса, CR – перенос как логическая переменная или сигнал на линии связи. Флаги представляют собой просто триггеры, связанные со схемой управления арифметическими операциями.
Двухадресное сложение (рис.5.3) дополнительных кодов проще одноадресного. Здесь операнды одновременно подаются на два входа сумматора, предварительное обнуление аккумулятора не требуется. Схема микропрограммы показана на рис 5.4. В ней принят логический способ контроля переполнения.
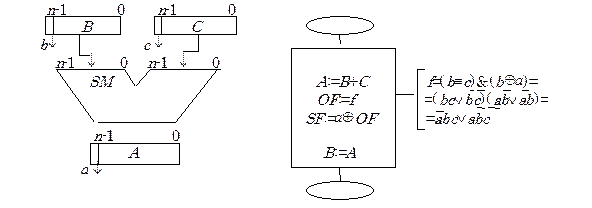
Рис. 5.3 Рис. 5.4
Посмотрим, насколько усложнится алгоритм сложения, если числа в регистрах В и С, а также окончательный результат находятся в прямом коде.
При одноадресном сложении знаковая цифра очередного операнда анализируется схемой управления. Если это нуль, то выполняется операция сложения этого операнда с содержимым аккумулятора (к началу операции он должен быть обнулен!). Если же знаковой цифрой является единица, то происходит сложение с обратным кодом операнда, который считывается с инверсных выходов соответствующего регистра. Чтобы обратный код превратить в дополнительный, в младший разряд сумматора нужно добавить единицу. Эта единица поступает по входу переноса в младший разряд.
По двухадресной схеме сложение чисел с одинаковыми знаками можно делать без обращения кода. При этом складываются модули, а знак суммы определяется логически. При несовпадении знаков слагаемых отрицательный операнд переводится в дополнительный код. При этом алгоритме сложения у сумматора отсутствует знаковый разряд. При сложении чисел с одинаковыми знаками триггер переноса CR контролирует переполнение, а при сложении чисел с противоположными знаками он определяет знак суммы. Ведь при сложении в дополнительном коде чисел с противоположными знаками перенос из старшего разряда получается, если сумма положительна или равна нулю. Контроль переполнения в случае противоположных знаков слагаемых не требуется.
Схема микропрограммы при двухадресном сложении получается сложнее, ввиду большего числа проверок логических условий, зато необходимое число последовательно выполняемых операций заметно сокращается. Микропрограммы сложения по обоим описанным способам приведены на рис. 5.5 (одноадресный вариант) и рис.5.6 (двухадресный вариант).
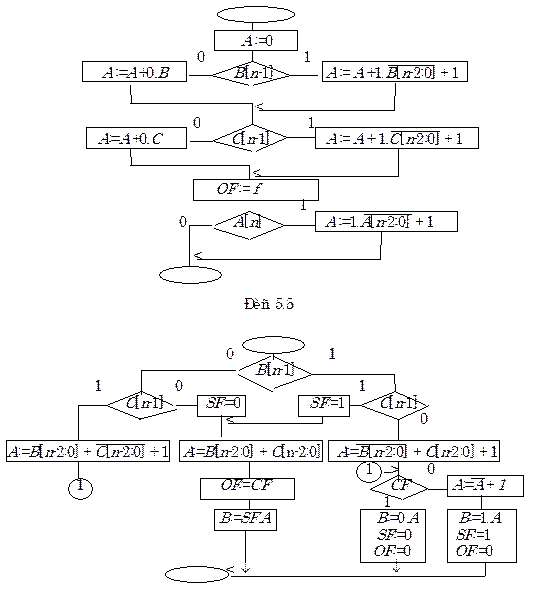
Рис. 5.6
 На рис. 5.6 показаны заключительные операции пересылки результата в регистр B и установки знакового флага SF.
На рис. 5.6 показаны заключительные операции пересылки результата в регистр B и установки знакового флага SF.
Дата добавления: 2020-06-09; просмотров: 777;











