Производная суммы, разности, произведения и частного функций
ПРОИЗВОДНАЯ ФУНКЦИИ. ГЕОМЕТРИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Определение производной
Определение производной. Пусть задана функция 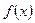 ,
, 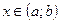 и пусть
и пусть 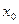 - некоторая точка интервала
- некоторая точка интервала 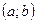 . Предел
. Предел
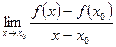
называется производной функции 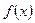 в точке
в точке 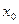 и обозначается
и обозначается 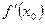 (если последний предел существует). Таким образом, по определению,
(если последний предел существует). Таким образом, по определению,
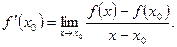
Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке. Функция 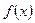 ,
, 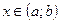 , имеющая в каждой точке интервала
, имеющая в каждой точке интервала 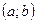 производную, называется дифференцируемой на этом интервале. Операция нахождения производной данной функции называется дифференцированием.
производную, называется дифференцируемой на этом интервале. Операция нахождения производной данной функции называется дифференцированием.
Обозначение производной функции 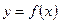 :
: 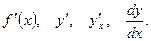
Если ввести приращение аргумента 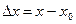 и приращение функции
и приращение функции 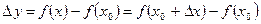 , определение производной запишется в виде
, определение производной запишется в виде
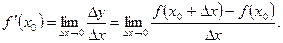
Так как 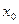 - произвольное значение аргумента, то можно обозначить его как x. Тогда получаем
- произвольное значение аргумента, то можно обозначить его как x. Тогда получаем
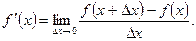
Пример:
Дана функция 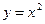 , найдите её производную.
, найдите её производную.
Решение.
а) 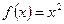 ,
, 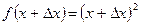 ,
,
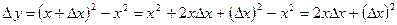
б) 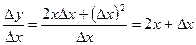
в) 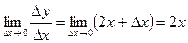
Таким образом, 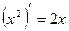 .
.
Производная суммы, разности, произведения и частного функций
Теорема 1. Если функции 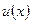 и
и 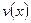 дифференцируемы на некотором интервале, то на этом интервале
дифференцируемы на некотором интервале, то на этом интервале
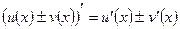
т.е. производная суммы (разности) функций равна сумме (разности) производных этих функций.
Теорема 2. Если функции 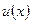 и
и 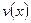 дифференцируемы на некотором интервале, то на этом интервале
дифференцируемы на некотором интервале, то на этом интервале
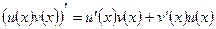 .
.
Следствие. Постоянный множитель можно выносить за знак производной, т.е. 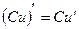 , где
, где 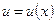 - дифференцируемая функция.
- дифференцируемая функция.
Теорема 3. Если функции 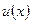 и
и 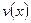 дифференцируемы на некотором интервале и
дифференцируемы на некотором интервале и 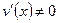 для любого x из этого интервала, то
для любого x из этого интервала, то
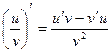 .
.
Дата добавления: 2020-06-09; просмотров: 596;











