Основы расчета подбивочного блока

Подбивочный блок – это вибрационное устройство, предназначенное для уплотнения балластного слоя под подошвами шпал. Шпалоподбивочный механизм блока имеет привод вибраций в виде эксцентрикового вала, соединенного через шатунные элементы с концами рычагов подбоек и механизм обжима балласта (подачи лопаток подбоек) в виде гидроцилиндров. Дополнительные приводы блока – механизм его вертикального перемещения (опускания с заглубоением подбоек и подъема) и механизм перемещения блока в поперечном направлении при работе в кривых и на стрелочных переводах.

Процесс уплотнения балластного слоя рабочими органами машин является сложным многофакторным процессом. Для его реализации взаимодействуют два сложных объекта: путевая машина и верхнее строение пути (в общем случае это РШР и балластная призма). На практике наибольшее распространение получил метод силового вибрационного воздействия с поступательным движением уплотнительной поверхности рабочего органа. Технические расчеты подбивочных блоков выполняются в целях оценки: производительности блока и машины, технологического эффекта работы блока через показатели качества уплотнения, усилий в элементах механизмов при расчете на прочность и надежность, параметров рабочих органов и режимов работы, характеристик энергоемкости при выборе параметров приводов экипажной части машины по характеристикам рабочих органов. Кроме того, производить оценку рабочих свойств верхнего строения пути при эксплуатации в требуемом режиме и др.

10.8.1. Взаимодействие лопаток подбоек и уплотняемого

балластного слоя

Кинематический и силовой анализ взаимодействия поступательно движущейся вибрирующей лопатки подбойки с массой балласта в слое рассмотривается на модели горизонтального вибрационного воздействие подбойки 1 с объемом балласта 3 под шпалой 2 (рис. 10.55). Угловая частота колебаний подбойки ω, рад/с, амплитуда A, м, а скорость подачи V_п, м/с.

При рассмотрении стационарного процесса взаимодействия подбойки с балластом начало отсчета времени можно принять в момент начала нового колебательного цикла. Тогда начальная фаза колебаний принимает нулевое значение. С этим моментом времени свяжем локальные системы координат 0St и 0Vt (рис. 10.56, а, б).

На рис. 10.56 левее точки начала координат 0 показаны части графиков, соответствующие предыдущему циклу, а правее – текущему циклу. При отрывном режиме работы [58] часть периода колебаний T лопатки находятся в контакте с балластом – с точки 1 графика до точки 2. Подбойка движется к шпале, производя обжим балласта. Пройдя точку максимального отклонения, подбойка начинает движение от шпалы, и в точке 2 ее скорость выравнивается со скоростью отдачи балласта V_б. В дальнейшем движении она отрывается от балласта. На участке 2-4 подбойка сначала движется от шпалы, а затем, пройдя точку 3 максимального отклонения, начинает движение к шпале. В точке 4, положение которой отражено на графике, подбойка встречается с балластом. Происходит удар лопатки о балласт, аналогичный удару в точке 1 предыдущего цикла.

Движение подбойки является результатом наложения ее колебательного и поступательного движений, условно показано в виде графика 1–2–3–4 (см. рис. 10.56, а). Уравнение лопатки подбойки в показанной локальной системе координат в абсолютном движении [58]:

(10.47)

Скорость движения лопатки подбойки, как производная по времени t от перемещения S_лп:

(10.48)

На участке 1–2 лопатка находится в контакте с балластом и производит его обжим. На этом участке совершается работа по уплотнению балласта, причем часть работы выполняет механизм привода вибраций, а часть работы механизм подачи. В точке 2 происходит отрыв лопатки от балласта, после чего она совершает возвратное движение, а балласт под действием сил упругости смещается. Уравнение смещения балласта:

(10.49)

где S₂ – отклонение лопатки с балластом от начального положения в точке отрыва 2, м; V_б – скорость отдачи балласта, м/с (V_б = 0,13 – 0,14 м/с); t₂ – время от начала цикла до момента отрыва, с.

Период колебаний T (T = 2π/ω), с, складывается из времени контакта t_к лопатки с балластом и времени ее отрыва t_о от балласта (T = t_к + t_о). В точке 4 положения лопатки (точка 4_б и точка 4_п, принадлежащие балласту и подбойке совпадают) наблюдается удар по балласту (см. рис. 10.56, а). При ударе происходят интенсивные смещения частиц балласта и его уплотнение, поэтому сначала определим t_к и t_о.

Момент времени отрыва лопатки подбойки от балласта:

(10.50)

Момент времени t₄ удара лопатки подбойки и уплотнения балласта определится из трансцендентного уравнения:

(10.51)

Это уравнение легко решается методом итераций. При итерационных вычислениях последовательно наращивается значение t₄ по формуле t₄=t₂+Δt (Δt – сколь угодно малый интервал наращивания времени, с). Итерации прекращаются, если левая часть уравнения станет ≤ 0.

Время отрыва и время контакта лопатки подбойки и балласта составляет: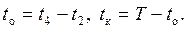

Скорость удара лопатки подбойки о балласт, м/с (см. рис. 10.56, б):

(10.52)

Для анализа силовых и энергетических соотношений процесса уплотнения балласта необходимо определить смещение лопатки подбойки S_к вместе с балластом, м:

(10.53)

где S_max – максимальное смещение лопатки с балластом относительно исходного расчетного положения (точка 0), м; S_п – величина подачи лопатки за цикл колебаний, м; S₄ – смещение лопатки относительно исходного положения в момент удара, м.

Максимальному смещению лопатки подбойки S_max соответствует его нулевая скорость, поэтому

(10.54)

где t_max – время от начала цикла до достижения лопаткой максимального отклонения, с.

Время, соответствующее максимальному отклонению лопатки, с

(10.55)

Величина подачи лопатки за цикл колебаний, м: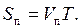

Смещение S_maxи S₄ определяются по (3.1) при подстановке соответствующих значений t_max и t₄.

Момент времени (точка 3), соответствующий минимуму траектории лопатки, с

(10.56)

Смещение S_min определится из подстановки t_min в (10.47). Моменту времени t_min соответствует максимум отрыва лопатки подбойки от балласта.

С учетом (10.49) максимальный отрыв лопатки от балласта:

(10.57)

На графике (см. рис. 10.56, а) величина S_min принимает отрицательное значение.

Таким образом, взаимодействие рабочего органа с балластом характеризуется полностью пятью параметрами [51, 59]: S_к – обжим (подача) балласта за каждый цикл колебаний (10.53), м; S_о – максимальный отрыв лопатки подбойки от балласта за цикл колебаний (10.57), м; t_о – время отрыва лопатки от балласта за цикл колебаний, с; t_к время контакта лопатки с балластом за цикл колебаний, с; V_у – скорость удара в момент встречи рабочей лопатки с балластом (10.52), м/с.

Для оценки характера взаимодействия лопатки с балластом используется параметр С режима уплотнения, значение которого с учетом упругой отдачи балласта определяется по формуле:

(10.58)

В числителе этого выражения приводится скорость взаимного сближения лопатки и балласта, а в знаменателе – амплитудное значение скорости вибрирования. Как показывает опыт эксплуатации уплотнительных рабочих органов машин, эффективное уплотнение происходит при взаимодействии лопатки и балласта с отрывом и ударами, это соответствует C < 1. При безотрывном режиме взаимодействия лопатки и балласта эффективность уплотнения резко падает, так как контакты частиц друг с другом малоподвижны, частицы оказываются взаимно заклиненными. При отрывном режиме взаимодействия контакты частиц становятся подвижными, имеют возможность перестроиться, образуя более плотную текстуру.

Экспериментально установлено, что результат уплотнения несвязного материала (щебня), выраженный через относительную осадку E_у, является случайной гиперболической функцией от общего количества относительных перемещений частиц материала, происходящих под действием внешних силовых импульсов с учетом сил инерции и внутреннего трения (активные перемещения), а также сил упругости и веса, вызывающих отдачу щебня при циклических разгрузках (пассивные перемещения), и выражается формулой [52]:

(10.59)

где χ = 0 – 2 – коэффициент, определяющий степень использования для уплотнения пассивных и активных относительных перемещений частиц; λ = 0 – 1 – коэффициент, определяющий долю объема материала, охваченного относительными перемещениями; (ωt_в)_min – минимально необходимое количество вибровоздействий для рабочих органов цикличного действия, умноженное на 2π; t_в – время воздействия на балласт, с; A, B – эмпирические коэффициенты, зависящие от рода уплотняемого материала и способов вибровоздействия. Для щебня при рациональных параметрах виброуплотнения χ = 2; λ = 1; A = 3300; B = 10, (ωt_в)_min = 600 – 800.

Выражение (10.59) является исходным для определения рациональных параметров виброуплотнения балласта. Эффективность виброуплотнения щебеночного балласта обеспечивается, если параметры взаимодействия и их соотношения составляют:

(10.60)

10.8.2. Расчет эффекта уплотнения балласта

подбивочным блоком

Требуемый результат уплотнения балластного слоя в зоне под шпалами достигается, в зависимости от ряда факторов, либо при однократном, либо при многократном виброобжиме балласта лопатками подбоек подбивочного блока (см. рис. 10.55).

Вначале определим относительную осадку уплотнения E_у объема балластного слоя под шпалой после однократного обжима. Пусть начальное состояние слоя характеризуется относительной осадкой уплотнения E_н. Отсутствует локализация зон уплотнения. Обжим объема балласта в слое толщиной h_сл, м, производится из положения лопаток, характеризуемого максимальным раскрытием S_max, м, в положение минимального раскрытия S_min, м (рис. 10.57). Подбивка (уплотнение балластного слоя в зонах под шпалами) производится с технологической выправочной подъемкой h_под, м. Начальный объем уплотняемой зоны, м³

(10.61)

где V_осн – основной объем балласта под шпалой, подлежащий уплотнению на длине (L_ш – e)/2, м; L_ш – длина шпалы, м (для железобетонной шпалы L_ш = 2,7 м, а для деревянной шпалы L_ш = 2,75 м), е – ширина не уплотняемой зоны в середине шпалы, м; V_доп – дополнительный объем балласта, м³, подаваемый подбойками в зону уплотнения при вибрационном обжиме с учетом угла передачи давления α_п, град.

Основной и дополнительный объемы:

(10.62)

(10.63)

где ψ = (0,9 – 1,0) – коэффициент притока (выдавливания) балласта при виброобжиме; k_доп = (1,2 – 1,3) – коэффициент, учитывающий дополнительную подачу балласта подбойкой за счет угла α_п передачи давления (для путевого щебня, подвергаемого вибрационному воздействию α_п = (15 – 20)º; J_под – число одновременно работающих в рассматриваемой зоне подбоек; d_п – начальный обжим балласта, равный толщине подбойки, м; k_п – коэффициент приведения площади лопатки, k_п = (a+d)(b+d)/(ab); F_р – рабочая площадь лопатки, F_р = ab.

Объем уплотненной зоны (ядра уплотнения), м³, характеризуемый искомой относительной осадкой уплотнения E_у, с учетом технологической подъемки h_под:

(10.64)

В модели фактически принимается в расчет одна и та же масса балластного материала, занимающая объем до уплотнения V_н, а после уплотнения объем V_у, поэтому результаты расчета по (10.61) и (10.64) для получения относительной осадки уплотнения необходимо подставить в (10.5).

Далее рассмотрим относительную осадку уплотнения E_у щебеночного балласта в ядре уплотнения под шпалой после двукратного виброобжима балласта подбойками. После первого обжима подбивочный блок приподнимается, лопатки подбоек выходят из балласта. Под действием вибраций при подъемке пути образующиеся пустоты заполняются обсыпающимся из шпальных ящиков балластом. При повторном обжиме образовавшиеся новые дополнительные объемы балласта должны заполнять ядро уплотнения.

Без разрушения сформированное в первом цикле ядро уплотнения может пополняться новыми объемами балласта только в случае, если его степень уплотнения ниже, чем формируемая в дополнительных объемах. В этом случае может происходить выравнивание (диффузия) степени уплотнения в ядре. Повторное уплотнение ядра не требуется при достижении степени уплотнения ядра, близкой к предельной.

В основу модели процесса повторного вибрационного обжима балластного слоя положена гипотеза, что происходит разрушение ядра уплотнения, сформированного после первого цикла и формирование нового ядра из двух объемов, характеризуемых разной степенью уплотнения. Кинематика движения лопаток подбоек и балластного слоя при втором обжиме идентична кинематике первого обжима, поэтому используем аналогичную расчетную схему (см. рис. 10.57).

Обозначим объемы, м³: V_н1 = V_осн; V_н2 = V_доп; V_у = V_осн, а соответствующие относительные осадки уплотнения в зонах: E_н1 = E_у(1); E_н2 = E_н. Для получения относительной осадки уплотнения E_у в ядре после второго цикла подставим полученные значения в формулу (10.6).

При многократном обжиме необходимо особое внимание обращать на наличие в балластной призме достаточного для получения требуемой степени уплотнения количества балластного материала. При недостатке материала в технологии работ должна быть предусмотрена дополнительная дозировка балласта и несколько проходов выправочно-подбивочной машины.

10.8.3. Расчет энергетических характеристик

приводов подбивочного блока

При обжиме балласта лопатка подбойки захватывает частицы по периметру, поэтому учитывается ее площадь и дополнительная площадь, образуемая частицами по периметру. Значение максимального усилия обжима балласта, кН:

(10.65)

где a, b – ширина и высота лопатки, м; d – средний диаметр частиц балласта, м (d = 0,04 м), k_п – коэффициент приведения площади лопатки, k_п = (a+d)(b+d)/(ab); F_р – рабочая площадь лопатки, F_р = ab.

Максимальное усилие обжима достигается в точке максимума смещения σ₄ лопатки (см. рис. 10.56, а). Работа по уплотнению балласта совершается на участке обжима от точки 1, соответствующей удару о балласт в предшествующем цикле, до точки максимума. Общее смещение S_к определяется по формуле (10.53) и обусловливается смещением, связанным с механизмом подачи S_кп и механизмом вибрации S_кв , м:

(10.66)

При обжиме балласта лопаткой подбойки в каждом цикле возрастает степень уплотнения. В начальном состоянии степень уплотнения характеризуется коэффициентом пористости ε_н, а после подачи подбойки на величину рабочего хода S_пп уплотненное состояние балласта соответствует коэффициенту пористости ε_у. Поэтому в момент касания подбойки и балласта в первом цикле и завершения последнего обжима реактивные усилия балласта (рис. 10.58):

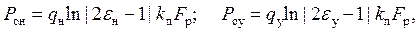(10.67)

где q_н, q_у – опытные коэффициенты для состояний балласта до и после уплотнения.

Работа в каждом цикле отражается площадями заштрихованных фигур, а общая произведенная работа уплотнения получается в результате их суммирования, кДж:

(10.68)

где k_у – коэффициент, учитывающий динамические явления при обжиме балласта и нелинейность нарастания реакции балласта при его обжиме, k_у = 0,8 – 1,0; k_бз – коэффициент, учитывающий трение боковых поверхностей лопатки и затекание балласта сзади лопатки при обжиме, k_бз – 1,2 – 1,5;

Средняя мощность, развиваемая приводом вибраций и подачи подбойки за время ее сведения, кВт:

(10.69)

Мощности, развиваемые механизмом вибраций и механизмом подачи, кВт:

(10.70)

10.8.4. Расчет усилий гидроцилиндров привода

подачи подбоек

Произведем определение усилий гидроцилиндров привода рычагов подбоек двухшпального подбивочного блока. Шпалоподбивочный механизм такого блока можно представить в виде четырех составляющих механизмов, которые связаны с одним эксцентриковым валом. Два из них располагаются снаружи, а два – внутри колеи. Привод вибраций подбоек одного из указанных механизмов, условно отраженных точками F и M (рис. 10.59), осуществляется через эксцентриковый вал, представленный в виде кривошипа AB (звено 2). Длина кривошипа равна эксцентриситету посадки шатунных подшипников. Гидроцилиндры отражаются поступательными кинематическими парами C и H, которые входят в шатунные звенья DBG и GK. Перемещаемые друг относительно друга части гидроцилиндров условно отражаются звеньями 3-1 и 3-2, 7-1 и 7-2. Рычаги вместе с подбойками представлены коромыслами DEF и KLM, которые через шарниры E и L установлены на станине блока EAL (стойка, состоящая из жестко связанных звеньев 1 и 5). Звенья, кроме того, между собой связаны вращательными кинематическими парами D, B, A, G, K, отражающими шарнирные узлы, коренные A и шатунные B подшипники эксцентрикового вала.

Степень подвижности такого механизма по формуле П.Л. Чебышева [1]:

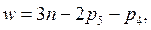(10.71)

где n – число звеньев механизма, исключая стойку; p₅, p₄, – число кинематических пар 5-го и 4-го классов.

В нашем случае n = 7, p₅ = 9, p₄ = 0, w = 3. Механизм имеет одну степень подвижности, позволяющую генерировать вибрации, и две степени подвижности, соответствующих реализации подачи лопаток подбоек при работе гидроцилиндров.C и H. В зависимости от решаемой задачи рассматриваемая схема может быть упрощена. При исследовании передачи вибраций лопаткам F и M в можно считать постоянными длины звеньев BD и GK. Кривошип 2 устанавливать в различные угловые положения с заданным шагом в пределах 0 – 2p, рад и исследовать перманентные угловые и линейные перемещения, скорости и ускорения звеньев, которые соответствуют вращению звена 2 с постоянной угловой скоростью w₂, рад/с. При перманентном движении кинематические характеристики звеньев зависят только от структуры механизма. При исследовании переходных процессов на перманентное движение накладывается начальное движение, соответствующее ускорению или замедлению вращения звена 2, от начального положения.

Для решения задачи определения усилий P_H и P_C, развиваемых штоками гидроцилиндров, условно «заморозим» их штоки относительно корпусов в положениях, соответствующих максимальным рабочим полезным нагрузкам P_F и P_M, условно приложенным в серединах лопаток подбоек. Получившиеся звенья обозначим цифрами 3 и 7. Для такого варианта механизма по (10.1) получим: n = 5, p₅ =7, p₄ = 0 и w = 1. Для решения задачи определения статических усилий необходимо аналитически определить положения всех звеньев механизма через углы j_I, где i = 1, 2,…8.

Рассматриваемый механизм является механизмом II класса [1], так как образован путем присоединения к механизму I класса (кривошипу 2) двух двухповодковых групп, образованных звеньями 3, 4 и звеньями 7, 8. Группа звеньев 7, 8 является присоединенной группой к группе 3, 4 через кинематическую пару вращения G. Для определения углов j_I необходимо решить векторные уравнения для замкнутых контуров ABDEA и ALKGBA.

Векторное уравнение контура ABDEA (обход контура против часовой стрелки):

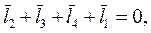(10.72)

где 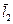, , 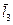, 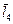– векторы, отражающие звенья 2, 3, 4, 1.

Этому векторному уравнению соответствует система уравнений в проекциях на координатные оси x и y:

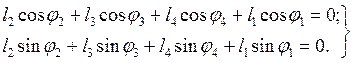(10.73)

В приведенном выражении длины звеньев, м, считаются заданными, также заданы углы , рад (H_AE и S_AE – координаты расположения шарнира E на стойке, м) и j₂ – угол поворота кривошипа 2, рад. Необходимо определить углы j₃ и j₄, рад. Положительное направление всех углов соответствует направлению вращения от оси x к оси y. Отсчет всех углов начинается от оси x, что дает возможность при необходимости вычислять абсолютные координаты, линейные и угловые ускорения и скорости.

После выполнения необходимого анализа [1] значения искомых углов, рад:

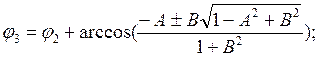(10.74)

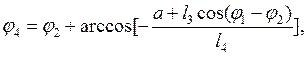(10.75)

где

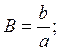
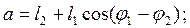
Векторное уравнение при обходе контура ALKGBA также против часовой стрелки:

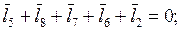(10.76)

где 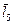, , 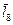, 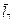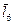– векторы, отражающие звенья 5, 8, 7, 6.

Соответствующая система уравнений в проекциях на оси x и y:

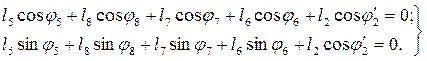(10.77)

Неизвестными в данном случае являются углы j₇ и j₈, рад. Угол j₆ определен по положению звена 3-6: 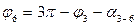(a_3-6 – тупой угол, образованный элементами 3 и 6 звена DBG, рад). 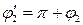– расчетный угол положения кривошипа при обходе против часовой стрелки контура ALKGBA, рад). В результате решения системы уравнений (10.29) получим:

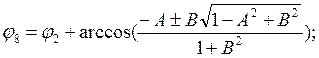(10.78)

(10.79)

где

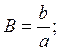
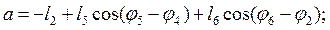
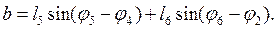
В этих выражениях угол 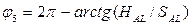– постоянный угол, характеризующий положение на стойке шарнира L.

Последовательным дифференцированием по углу j₂ выражений (10.74), (10.75), при необходимости, определяются абсолютные угловые скорости w_I, рад/с и угловые ускорения e_I, рад/с² звеньев. Путем составления планов скоростей находятся абсолютные и относительные скорости необходимых для дальнейшего анализа точек звеньев механизма, а планов ускорений – соответствующие ускорения.

После определения масс и моментов инерции звеньев относительно центров масс можно решать широкий круг задач кинетостатического и динамического анализа механизмов привода рычагов подбоек: определять уравновешивающие силы, приложенные к звену приведения, пользуясь методом рычага Н.Е. Жуковского; определять моменты инерции маховиков для обеспечения заданной равномерности вращения эксцентрикового вала; определять статические и динамические нагрузки на звенья без учета и с учетом трения в кинематических парах и другие задачи.

Для решения поставленной задачи оценки усилий в гидроцилиндрах привода рычагов подбоек упростим дальше расчетную модель, считая, что l₂ = 0 (пренебрегаем эксцентриситетом вибровала) и j₂ = 0 – безразлично, в каком положении находится кривошип с нулевой длиной. При силовом анализе механизмов рекомендуется начинать с самой последней присоединенной группы Ассура [1]. В нашем случае это шатунное звено 7 и коромысло 8-10. В точке M приложена полезная нагрузка P₁₀, кН, соответствующая результирующей силе реактивного давления балласта на лопатки двух наружных подбоек. Она определяется из расчета взаимодействия подбоек и балласта. Считаем, что эта сила всегда нормальна к рабочей поверхности подбойки и к направлению звена 10. Статическая составляющая силы P_H определится из уравнения равновесия моментов относительно шарнирного узла L. После составления и решения этого уравнения получим усилие гидроцилиндра H, кН:

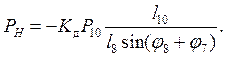(10.80)

Для первой присоединенной группы Ассура, состоящей из шатунного звена 3-6 и коромысла 1-9, к точке F которого приложена полезная нагрузка P₉, кН, можно произвести аналогичные рассуждения и получить выражение для статической силы гидроцилиндра C, кН:

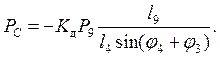(10.81)

В последних формулах K_д = 1,5 - 2,0 – коэффициент, учитывающий динамический характер работы гидроцилиндров.

Кинематический анализ позволяет связать величину раскрытия подбоек S (рис. 10.60) с длинами l₉, l₁₀ нижних частей коромысел, отражающих рычаги подбоек. Текущее раскрытие подбоек составит 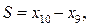м, где 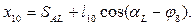(j_4(с) – угол поворота звена 4, отражающего рычаг внутренней подбойки смежного механизма блока).