Получение экспериментальных зависимостей для расчета

Применение рекомендованных расчетных зависимостей для определения параметров процессов теплообмена в пищевых производствах не всегда оправдано. Дело в том, что они получены, как правило, путем обработки экспериментальных данных, относящихся к другим областям техники. На процессы пищевых производств их переносят приближенно, и оценки допускаемых при этом погрешностей часто затруднительны.

Радикальным путем уточнения расчетных зависимостей может стать использование собственных экспериментальных данных, получаемых непосредственно исследователем по следующим методикам:

на экспериментальных или натурных образцах оборудования воспроизводят расчетные условия воздействия факторов окружающей среды на изделие;

изделие дооснащают необходимыми измерительными средствами и имитаторами внешних воздействий;

воспроизводят расчетный технологический процесс и измеряют все действующие параметры;

результаты измерений обрабатывают, т. е. аппроксимируют расчетными зависимостями с уточнением постоянных коэффициентов.

В большинстве случаев исследования стараются проводить на натурных образцах оборудования с заменой обрабатываемых изделий имитаторами. Например, для уточнения зависимостей передачи теплоты в печи к изделию (булочке), выпекаемому на поду, исследования могут быть выполнены на натурной печи с использованием имитатора булочки, размещенного на имитаторе пода.

Схема экспериментальной установки для исследования теплопередачи при выпекании изделия (булочки) приведена на рисунке 24.4.

Имитатор пода изготовляют в виде плоской поверхности, копирующей по геометрическим размерам часть пода. Снизу к нему

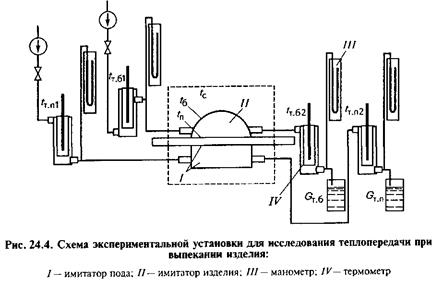
прикрепляют коллектор поддержания заданной температуры пода. В коллектор подается и из него отводится теплоноситель, изменением расхода которого будет регулироваться температура пода. Имитатор пода снабжают средствами измерения: температуры пода tn;

температур теплоносителя на входе и выходе из имитатора пода

расхода теплоносителя пода

Поступающий к изделию тепловой поток в данном примере может быть представлен в виде двух составляющих. Одна из них входит через под (дп), а вторая — через поверхность, соприкасающуюся с окружающей средой (дс). Основной методический прием получения экспериментальных данных для последующей аппроксимации расчетными формулами — это создание условий для исключения поступления второго теплового потока к имитатору изделия. Константы расчетных формул находят из условия совпаде­ния расчетных и экспериментальных значений физических величин в отдельных точках. Избыточные результаты эксперимента используют для уточнения диапазона применимости полученной расчетной формулы по варьируемым параметрам.

Имитатор булочки изготовляют из теплопроводного тонколистового материала. По форме он копирует выпекаемое изделие. Его снабжают штуцерами подвода и отвода теплоносителя к внутренней полости и средствами измерения:

температуры наружной поверхности имитатора изделия (булочки) со стороны окружающей среды %;

температур теплоносителя на входе в имитатор изделия и на выходе из него;

расхода теплоносителя через имитатор изделия

Измеряют также температуру окружающей среды в печи tc и скорость ее движения в расчетной точке, м/с.

Для устранения теплового потока к имитатору изделия через под печи путем изменения расхода теплоносителя через коллектор пода уравнивают температуры теплоносителей в обоих имитаторах. При этом тепловой поток (Вт) к изделию передается только через верхнюю часть имитатора и определяется по формуле ператур окружающей среды и поверхности выпекаемого изделия, а функция — искомые потоки теплоты. В зависимости от степени аппроксимирующего полинома в одной или нескольких точках (при одном или нескольких значениях аргумента) имеет место полное совпадение расчетных и экспериментальных данных. При отклонениях аргумента от этих значений погрешность аппроксимации увеличивается. Чем ближе функция аппроксимирующего полинома к истинной или аппроксимируемой, тем шире область ее применения.

Если расчетную формулу для этого потока теплоты (Вт) представить в виде

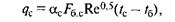
и учесть, что показатель степени 0,5 при относительной скорости обдува изделия (при критерии Рейнольдса) соответствует рекомендованному выше, то аппроксимирующий коэффициент теплоотдачи [Вт/(м² • К)] определится по формуле

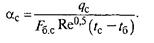
В результате исследований теплоотдачи к выпекаемым булочкам массой 200 г в условиях пекарского шкафа с принудительным движением воздуха в нем со скоростями 1...8 м/с в диапазоне температур среды шкафа и пода печи до 250 °С получено значение коэффициента теплоотдачи

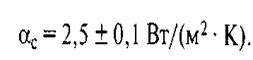
Изложенная методика аппроксимации экспериментальных данных расчетными выражениями представляет собой известную математическую процедуру аппроксимации экспериментальных данных полиномами. В соответствии с методикой составления феноменологических зависимостей аргументом аппроксимирующего полинома служит обобщенная действующая сила, а функцией — искомая функция. В данном случае аргумент — это разность температур.

Основные положения

1. Сложные тепловые процессы слагаются из трех простых: теплопроводности, конвекции и тепловой радиации. Теплопроводность - передача механической энергии при соударениях молекул. Конвекция перенос теплоты вместе с нагретыми элементами среды. Тепловая радиация - передача теплоты путем излучения и поглощения электромагнитных волн поверхно­стями тел.

2. Как простые, так и сложные тепловые процессы описываются феноменологическими зависимостями, которые открыты ранее и получили имена ученых: Фурье, Ньютона-Рихмана и Стефана- Больцмана.

3. В расчетах тепловых потоков, передаваемых в теплообменных аппаратах, необходимо учитывать непостоянство разности температур теплоносителей по площади теплопередачи. Для этого расчет строят либо поэлементно, считая разность температур для каждого элемента постоянной, либо осредняют ее. Учитывая, что в подавляющем большинстве теплообменных аппаратов температуры теплоносителей изменяются экспоненциально по координатам, разность их температур осредняют по логарифмической зависимости.

4. Технологические расчеты теплообменников сводятся к решению уравнений баланса масс и энергий. Физический смысл этих балансов - равенство сумм массовых (энергетических) потоков, поступающих в аппарат и уходящих из него. Как правило, вещество и энергия входят в аппарат и уходят из него, переходя из одного потока в другой, но их суммарные расходы остаются неизменными. В энергетических балансах учитывают потоки теплоты, теряемой через ограждения аппаратов.

5. В расчетах энергетических потоков используют понятие энтальпии. Энтальпия складывается из энергии, аккумулированной (запасенной) телом, и энергии, которая может высвободиться или поглотиться при фазовом переходе, растворении, сорбции или в другом процессе, реализующемся параллельно с теплообменом.

Контрольные вопросы и задания.

1. Какие вы знаете простые процессы теплообмена? 2. Приведите примеры сложных процессов теплообмена. 3. Что является обобщенной движущей силой процесса теплоотдачи от греющего пара к нагреваемой стенке теплообменника? 4. Что такое энтальпия? 5. Для чего вычисляют среднюю разность температур теплоносителей в теплообменнике? 6. Почему среднюю разность температур теплоносителей вычисляют как среднюю логарифмическую? 7. Можно ли назвать зависимость для вычисления тепловых потоков феноменологической? 8. Напишите феноменологическую зависимость для вычисления теплового потока в любом сложном процессе теплопередачи. 9. В чем сущность энергетического баланса любого теплового аппарата?