Использование феноменологического метода при расчёте тепловых процессов
Феноменологические методы широко применяют для расчетов теплопередачи в технологической аппаратуре. В них используют уравнения балансов тепловых и массовых потоков вещества и эмпирические связи между ними; общие закономерности теплопередачи преобразуют к виду, удобному для данного метода расчетов.
Определив из уравнений теплового баланса тепловой поток Q, передаваемый в теплообменном аппарате, и ограничения на его поверхностную плотность q, которые, как правило, накладываются технологическими соображениями соответствующего производства, находят необходимую площадь теплообменных поверхностей F= Q/q. Возможно наложение технологических ограничений не непосредственно на q, а на однозначно связанные с ней параметры, например на температуру теплоотдающей поверхности. Ограничения определяются условиями термической стойкости продукта.

Уравнения теплового баланса для передаваемого теплового потока в большинстве теплопередающих аппаратов, в которых теплота от одного теплоносителя передается другому, имеют вид
Феноменологические методы широко используют для определения тепловых потоков, передающихся в соответствующих условиях как в простых, так и в сложных тепловых процессах. Эти соотношения формулируются идентично для всех условий. Они констатируют пропорциональность соответствующих тепловых потоков и побуждающих их сил.
Для примера рассмотрим теплопередачу через покрытую накипью плоскую стенку (рис. 24.2).
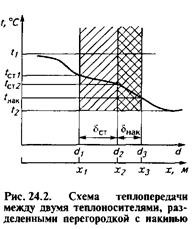
Для условий теплопроводности в соответствии с законом теплопроводности Фурье это соотношение имеет вид
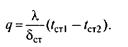
Индексы принадлежности параметров: 1,2 — первому и второму теплоносителям; стенке; накипи.
Для процесса теплоотдачи от жидкости (газа) твердой стенке справедлив закон теплоотдачи Ньютона—Рихмана:
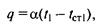
где λ — коэффициент теплоотдачи, Вт/(м2 • К); t — температуры среды и стенки, °С;
для теплоотдачи от покрытой накипью плоской разделяющей стенки к окружающему воздуху — также закон теплоотдачи Ньютона—Рихмана:
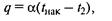
где tнак, t2 — температуры наружной стенки и окружающей среды;
 |
Во всех четырех уравнениях тепловой поток, передающийся в данной системе, одинаков. На основании этого получим
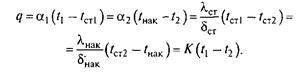
Учитывая, что общий температурный напор в данной модели теплопередачи {t1 -t2) складывается из температурных напоров, необходимых для передачи удельного теплового потока через каждый из рассматриваемых слоев, препятствующих передаче теплоты, получим
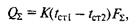
где к — коэффициент теплопередачи, Вт/(м2 ■ К); fΣ — суммарная площадь стенки в направлении, нормальном потоку теплоты, м2.
Введем обозначения
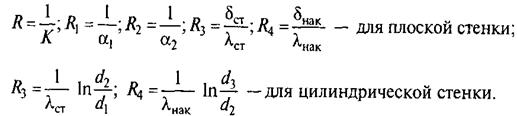
Величины R1 R2, R3, R4 имеют физический смысл и названия соответствующих термических сопротивлений, м2 • К/Вт. В этих обозначениях имеем
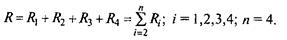
Величины, обратные термическим сопротивлениям, называют термическими проводимостями.
Если в данном примере стенка является цилиндрической, то выражения для коэффициентов теплоотдачи меняются лишь количественно; форма записи законов теплопередачи при этом сохраняется. Выражения же для теплопроводности при этом изменяются, и формула для коэффициента теплопередачи К принимает вид
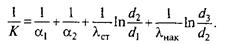
Обратим внимание на то, что в любой системе, если задан тепловой поток q, распределение температур автоматически .
Если в рассматриваемом примере анализировать только часть процесса, например только теплопередачу от среды к твердой поверхности и далее внутрь тела, то выражения для теплового потока часто преобразуют к форме
Дата добавления: 2016-06-29; просмотров: 2399;











