Определение скоростей точек плоской фигуры с помощью МЦС.
Если мгновенный центр скоростей Р найден и если известна угловая скорость фигуры, то скорость любой точки В фигуры определяется как скорость этой точки во вращательном движении вокруг МЦС, т. е. вектор 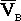 перпендикулярен к отрезку РВ и по модулю равен w×РВ. Отсюда следует, что скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей, т. е.
перпендикулярен к отрезку РВ и по модулю равен w×РВ. Отсюда следует, что скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей, т. е. 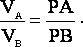
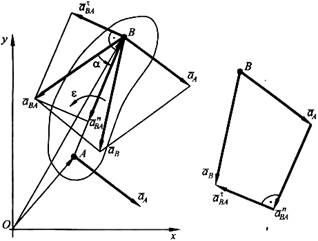
Соотношение между ускорениями двух точек плоской фигуры при плоском движении.
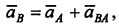 т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при вращательном движении плоской фигуры вокруг полюса.
т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при вращательном движении плоской фигуры вокруг полюса.
Ускорение точки В вокруг А состоит из касательной и нормальной составляющих: 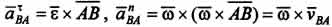 , модули которых
, модули которых 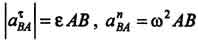 .
.
Касательное ускорение направлено перпендикулярно отрезку АВ в сторону, указанную дуговой стрелкой углового ускорения.Нормальное ускорение направлено от точки В к полюсу А. Таким образом, 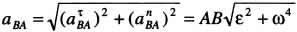 .
.
Обозначив угол между ускорением точки В вокруг А и отрезком АВ через "альфа", найдем: 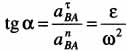 .
.
Дата добавления: 2018-11-26; просмотров: 1621;











