Теорема о проекциях скоростей двух точек твердого тела на прямую, проходящую через эти точки.

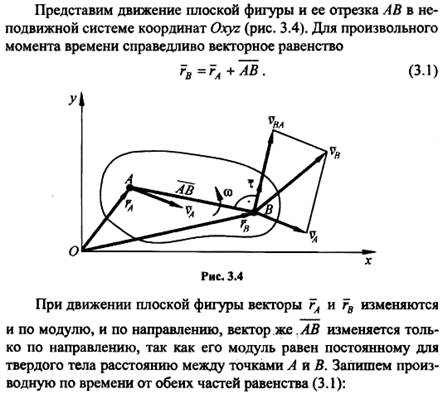
Соотношение между скоростями двух точек плоской фигуры при плоском движении твердого тела.

Способы определения угловой скорости при плоском движении.

Дополнение:

Мгновенный центр скоростей (МЦС). Способы нахождения.

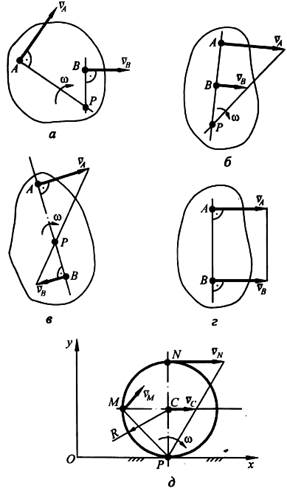
В любой момент времени при плоском движении фигуры существует единственная точка фигуры, скорость которой равна нулю. Эту точку называют мгновенным центром скоростей
(МЦС). Найдем эту точку, обозначив ее Р.

Примем точку Р за полюс фигуры. Тогда для ее произвольной точки В можно записать: 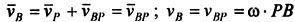, где PB — расстояние от МЦС — точки Р до точки В; вектор vB перпендикулярен отрезку РВ, направлен в сторону вращения фигуры вокруг МЦС (см. рис. 3.5), а его модуль пропорционален расстоянию от МЦС до точки.

Таким образом, скорости точек плоской фигуры в данный момент времени вычисляются так же, как если бы фигура вращалась вокруг неподвижной оси, проходящей через МЦС перпендикулярно плоскости движения, с той же угловой скоростью "омега".