Морская картография

Морские карты, руководства и пособия для мореплавания, издаваемые ГУНиО МО РФ явля-ются официальными документами, содержа-щими сведения о навигационно-гидрографических элементах в районах океанов и морей и прилега-ющих к ним побережий. Они предназначены для решения задач мореплавания и морского про-мысла.

Картой называется уменьшенное обобщённое изображение поверхности Земли и её отдельных участков на плоскости с помощью условных зна­ков.

Поверхность Земли на плоскости изобра-жают по определённым математическим зако-нам. Способ изображения поверхности Земли на плоскости называется картографической проек-цией. В общем виде картографическая проекция определяется двумя уравнениями:

x = f1(φ,λ), y = f2(φ,λ),

где φ и λ – географические координаты точки на поверхности Земли;

x и y – прямоугольные координаты той же точки на плоскости.

Функции f1 и f2 определяют свойства карто-графической проекции.

Изображение системы меридианов и парал-лелей на карте называется картографической сеткой. Картографическая сетка, которая изо-бражается на карте наиболее просто, называ­ется нормальной сеткой. Это либо две системы параллельных прямых, пересекающихся под углом 90º, либо концентрические окружности и их ра­диусы.

Кроме нормальной, существуют косая и попе­речная картографические сетки, на которых ме­ридианы и параллели изображаются сложными кривыми линиями.

Масштаб карты

Основной характеристикой карты в любой проекции является масштаб.

Главным масштабом Мо, называется отно-шение, показывающее, в сколько раз уменьшены линейные размеры поверхности Земли, при изо-бражении её на карте. Главный масштаб отно-сится к какой-либо линии или точке на карте и указывается в заголовке карты.

Вследствие искажений, возникающих при изо-бражении выпуклой поверхности Земли на плос-кости, масштаб в других точках карты отли-чается от главного, и называется частным мас-штабом М.

М = ds/dS,

где ds – бесконечно малый отрезок на карте;

dS – соответствующий ему отрезок на ме­стности.

В общем случае, частный масштаб зависит от направления.

Частный масштаб вдоль меридиана обозна-чается m, а вдоль параллели n.

В любой точке проекции частный масштаб по двум определённым взаимно перпендикулярным направлениям имеет экстремальные значения

Мmax = a; Mmin = b.

Эти направления называются главными на­правлениями. В нормальных картографических проекциях главные направления совпадают с ме­ридианами и параллелями.

Классификация

картографических проекций

Картографические проекции классифицируют по двум признакам:

- по характеру искажений;

- по виду нормальной картографической сетки.

По характеру искажений проекции делятся на следующие:

- равновеликие (эквивалентные);

- равноугольные (конформные);

- равнопромежуточные;

- произвольные.

В равновеликих (эквивалентных) проекциях сохраняется неизменным масштаб площадей, то есть отношение бесконечно малой площади на карте к соответствующей площади на местно­сти. При этом масштабы по главным направле­ниям отвечают условию

a · b = const.

Однако, у равновеликих проекций нарушается подобие фигур, искажаются направления и углы.

В равноугольных (конформных) проекциях со­храняется подобие бесконечно малых фигур. Ча­стные масштабы по всем направлениям в каж­дой данной точке карты у них одинаковы:

m = n = const.

Углы на карте у равноугольных проекций равны соответствующим углам на местности. Однако, у них искажается соотношение площа­дей.

В равнопромежуточных проекциях сохраня­ется неизменным масштаб длин по одному из главных направлений, то есть

a = const или b = const.

Все остальные проекции относятся к произ­вольным.

По виду нормальной картографической сетки проекции делятся на следующие:

- цилиндрические;

- конические;

- азимутальные;

- производные.

В цилиндрических проекциях меридианы и параллели нормальной картографической сетки изображаются в виде двух систем параллельных прямых, пересекающихся под углом 90º.

Уравнения этих проекций в общем виде

x = f(φ); y = αλ.

Вид функции f(φ) и величина параметра про­екции α определяют характер искажений.

Геометрически построение цилиндрической проекции можно интерпретировать так: по­верхность земного шара проецируется на ци­линдр, затем цилиндр разворачивается в плос­кость.

Нормальная (прямая) цилиндрическая проекция – оси Земли и цилиндра совпадают.

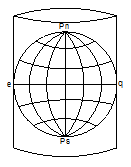
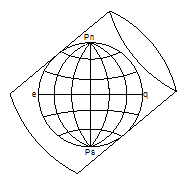
Косая цилиндрическая проекция – оси Земли и цилиндра составляют угол больше 0º и меньше 90º.

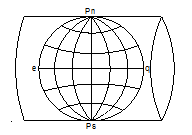
Поперечная цилиндрическая проекция – ось цилиндра совпадает с плоскостью экватора.

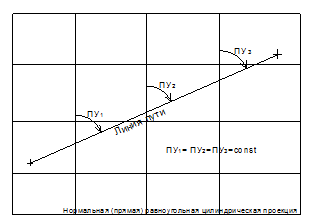
Цилиндрические проекции могут быть равно­угольными, равновеликими и равнопромежуточ­ными.

Нормальная (прямая) равноугольная цилиндри­ческая проекция применяется для составления морских навигационных карт (МНК), так как на ней сохраняется равенство углов (курсы, пеленги, путевые углы) и линия пути, если судно следует постоянным курсом, изображается на карте прямой линией, что существенно упрощает веде­ние навигационной прокладки.

В конических проекциях параллели нормальной картографической сетки изображаются в виде дуг концентрических окружностей, а меридианы в виде их радиусов, причём углы между радиусами пропорциональны соответствующим разностям долгот.

Так же как и цилиндрические, конические про­екции могут быть равноугольными, равновели­кими и равнопромежуточными, а также нор­мальными (прямыми), косыми и поперечными.

Конические проекции используются для изображения большого района океана, а так же для составления аэронавигационных карт.

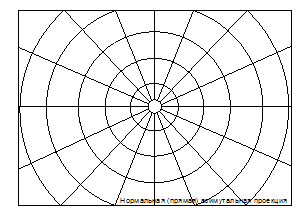
В азимутальных проекциях параллели нормальной картографической сетки изобража­ются в виде концентрических окружностей, а меридианы их радиусами, причём углы между радиусами равны соответствующим разностям долгот.

Азимутальные проекции используются для изо­бражения полярных областей, для составления карт полушарий в атласах, а также для морских специальных и вспомогательных карт.

Меркаторская проекция

Большинство МНК составляется в прямой (нормальной) равноугольной цилиндрической про­екции Меркатора. На ней линия пути (локсодро­мия) изображается в виде прямой и сохраняется равенство углов. Эти свойства упрощают гра­фическое решение задач на карте.

Геометрическая интерпретация построения меркаторской проекции следующая.

Поверхность Земли проецируется на каса-тельный по экватору цилиндр. При этом меридианы разгибаются до прямых линий, а па­раллели растягиваются до размеров экватора. Величина растяжения каждой параллели тем больше, чем дальше от экватора она располо­жена – пропорционально secφ.

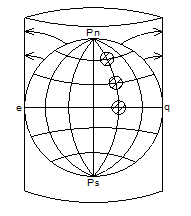
Затем цилиндр разворачивается в плоскость. Полученная проекция является прямой цилиндри­ческой, но не равноугольной.

Три фигуры в форме круга одинаковой площади на поверхности Земли получили разные изобра­жения на проекции. Фигура, расположенная на экваторе, не исказилась, а два других круга рас­тянулись в эллипсы. Причём, величина растяже­ния пропорциональна secφ.

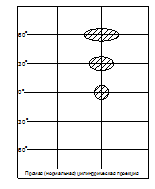
У равноугольной проекции должно сохра­няться подобие фигур, то есть изображения в нашем примере должны иметь форму круга. Для этого необходимо также растянуть и мери­дианы, причем растяжение меридианов должно быть неравномерным по всей их длине, а пропор­циональным secφ.

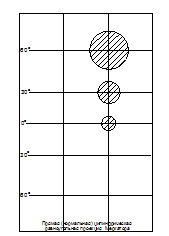В результате получим прямую (нормальную) цилиндрическую равноугольную проекцию Мерка­тора. Подобие фигур сохранилось, однако нару­шилось соотношение площадей.

Свойства равноугольности и равновеликости несовместимы.

Если Землю принять за шар, то уравнения меркаторской проекции имеют вид:

x = 2,3026·lg tg(45º + 0,5φ);

y = R·λ,

где R – радиус земного шара.

С помощью уравнений проекции по заданным географическим координатам точки можно вы­числить плоские прямоугольные координаты этой точки на карте.

При расчётах картографической сетки и гра­фических построениях на карте используется меридиональная часть МЧ:

D = 7915,704·lg tg(45º + 0,5φ);

МЧ это расстояние по меридиану от эква­тора до данной параллели в нормальной равно­угольной цилиндрической проекции Меркатора, выраженное в экваториальных минутах при масштабе на экваторе равном единице. Отрезок меридиана на меркаторской карте, выраженный в экваториальных минутах, определяется разно­стью меридиональных частей РМЧ.

Меркаторская проекция равноугольная, по­этому масштаб в каждой точке карты по всем направлениям одинаков, однако, величина его из­меняется в зависимости от широты, а вдоль каждой параллели он постоянен.

Если в качестве главной параллели принять экватор, то частный масштаб изменяется про­порционально secφ:

М = Мэ secφ.

Следовательно, на меркаторских картах вблизи экватора частный масштаб мало отлича­ется от главного и изменяется медленно. В высо­ких широтах частный масштаб изменяется очень быстро вследствие чего большие искаже­ния площадей, и использование меркаторской проекции становится невозможным.

На горизонтальных сторонах рамки карты (верхней и нижней) разбивается шкала долгот. Так как меридианы на меркаторской карте па­раллельны между собой, то длины одной минуты всех параллелей, в том числе и экватора одина­ковы, поэтому длину минуты параллели е исполь­зуют в качестве единицы длины при графических построениях. Величина е называется единица карты.

Величина одной минуты меридиана на мерка­торской карте называется меркаторской милей. Длина меркаторской мили увеличивается с увели­чением широты. Поэтому при измерении рас­стояний на карте необходимо пользоваться шка­лой вертикальной рамки в той широте, где нахо­дится измеряемый отрезок.