Метод узловых потенциалов
В методе узловых потенциалов сначала определяются потенциалы всех узлов схемы по отношению к одному из узлов, потенциал которого условно принимается равным нулю. Далее с помощью закона Ома для участка цепи с источником ЭДС рассчитываются токи в ветвях схемы.
Покажем возможность такого подхода. Рассмотрим схему рис. 27.
Схема содержит семь ветвей и четыре узла. Параметры схемы известны. Требуется определить токи ветвей.
Заземлим один из узлов схемы, например, узел c и примем его потенциал равным нулю (φc = 0). Для определения потенциалов оставшихся (n – 1) узлов необходимо составить систему из (n – 1) уравнения относительно неизвестных потенциалов.
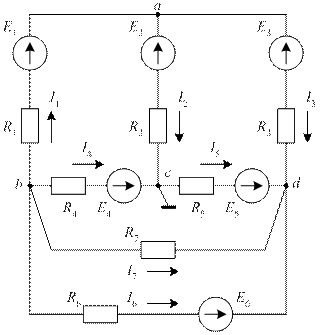
Рис. 27. К методу узловых потенциалов
Для вывода этой системы зададимся положительными направлениями токов в ветвях и для узлов a, b, d (рис. 27) составим уравнения по первому закону Кирхгофа:
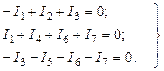
Полученная система из трех уравнений содержит семь неизвестных токов и решения не имеет. Необходимо свести ее к системе из трех уравнений с тремя неизвестными. В качестве таких неизвестных целесообразно представить потенциалы узлов a, b, d.Выразим токи ветвей через потенциалы узлов, ЭДС источников и проводимости ветвей:
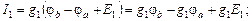
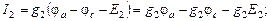
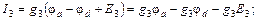
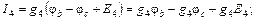
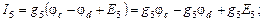
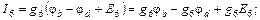
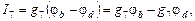
где потенциалы φa, φb, φd пока неизвестны, потенциал φc = 0, а проводимости ветвей есть величины обратные сопротивлениям ветвей
g1 = 1/R1, g2 = 1/R2, g3 = 1/R3, g4 = 1/R4, g5 = 1/R5, g6 = 1/R6, g7 = 1/R7.
Подставив выражения для токов ветвей в исходную систему уравнений, сгруппировав в левой части члены, содержащие неизвестные потенциалы φa, φb, φd, и перенеся в правую часть члены, не содержащие неизвестных величин, получим следующую систему уравнений
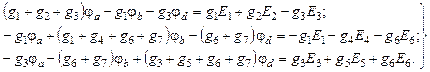
Эту систему уравнений можно записать иначе в общем виде, справедливом для любой схемы с четырьмя узлами
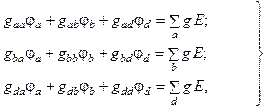
где gaa, gbb, gdd – собственные проводимости узлов a, b, d (суммы проводимостей ветвей, входящих в каждый из этих узлов); gab=gba, gad=gda, gbd=gdb – смежные проводимости узлов a, b, d (суммы проводимостей ветвей, соединяющих пары узлов, взятые со знаком минус).
В правых частях уравнений рассматриваемой системы берутся алгебраические суммы произведений gE для ветвей, входящих соответственно в узлы a, b, d. Причем члены этих сумм берутся со знаком плюс, если стрелка источника ЭДС направлена к соответствующему узлу, и со знаком минус, если стрелка направлена от узла.
Из решения рассматриваемой системы уравнений определяются потенциалы узлов a, b, d, а по ним с помощью закона Ома для участка цепи с источником ЭДС – токи ветвей.
Рассматриваемую систему уравнений можно представить в матричной форме, обобщив ее для случая схемы с n = y + 1узлами
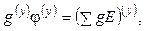
где g(y) – квадратная матрица узловых проводимостей;
φ(y) – матрица-столбец узловых потенциалов;
(ΣgE)(y) – матрица-столбец алгебраических сумм произведений gE.
Общее решение системы линейных алгебраических уравнений порядка y относительно любого из узловых потенциалов, например, потенциала l-го узла можно записать в виде следующего выражения:
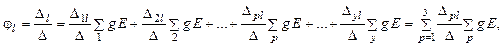 где Δ – определитель матрицы узловых проводимостей; Δl – дополнительный определитель, который составляется из определителя Δ за счет замены в нем столбца l столбцом свободных членов; Δpl – алгебраическое дополнение, получаемое из определителя Δ путем исключения столбца l и строки p и умножения получающегося минора на (–1)р+l.
где Δ – определитель матрицы узловых проводимостей; Δl – дополнительный определитель, который составляется из определителя Δ за счет замены в нем столбца l столбцом свободных членов; Δpl – алгебраическое дополнение, получаемое из определителя Δ путем исключения столбца l и строки p и умножения получающегося минора на (–1)р+l.
Методика расчета по методу узловых потенциалов.
1. Задаемся положительными направлениями токов в ветвях схемы.
2. Заземляем один из узлов схемы и приравниваем его потенциал нулю.
3. Составляем систему уравнений для определения потенциалов оставшихся узлов. Число уравнений в системе должно быть равно числу узлов минус единица. Каждое уравнение системы составляется для своего узла. В левой части уравнения записывается алгебраическая сумма произведения собственной проводимости узла на потенциал этого узла и произведений смежных проводимостей на потенциалы узлов, связанных ветвями с рассматриваемым узлом. (Собственные проводимости узлов – положительные величины, смежные проводимости - отрицательные величины). В правой части каждого уравнения системы записывается алгебраическая сумма произведений вида gE для ветвей, входящих в рассматриваемый узел и содержащих источники ЭДС. При этом соответствующие gE берутся с плюсом, если источник ЭДС направлен к рассматриваемому узлу, и с минусом, если источник ЭДС направлен от узла.
4. Решается система уравнений, и определяются узловые потенциалы.
5. С помощью закона Ома для участка цепи с источником ЭДС определяются токи ветвей.
Примечания. 1) Собственные и смежные проводимости узлов определяются на основе проводимостей ветвей (не элементов, а ветвей!). Поэтому если ветвь содержит несколько включенных последовательно сопротивлений (в том числе и внутренних сопротивлений источников), то вначале нужно найти результирующее сопротивление ветви как сумму всех последовательно включенных сопротивлений ветви. А затем определить проводимость ветви как величину обратную результирующему сопротивлению ветви. Например, если в первой ветви схемы рис. 27 источник ЭДС не идеальный и характеризуется некоторым внутренним сопротивлением источника Ri1, то результирующее сопротивление первой ветви равно R1 + Ri1, и проводимость первой ветви находится как g1= 1/( R1 + Ri1).
2) При наличии в схеме идеальных источников тока правые части уравнений системы в алгебраических суммах ΣgE будут содержать также токи идеальных источников тока Ik, если ветвь с источником тока входит в рассматриваемый узел. Выбор знака для источника тока такой же, как и для источника ЭДС. Проводимости ветвей, содержащих идеальные источники тока, равны нулю, т.к. внутреннее сопротивление источника тока равно бесконечности.
Метод узловых потенциалов эффективен, если число узлов схемы, уменьшенное на единицу, меньше числа независимых контуров. В противном случае более эффективен метод контурных токов.
Пример 2. Рассчитать токи в ветвях схемы рис. 28 методом узловых потенциалов, вычислить напряжения на зажимах источников, и для контура, содержащего два источника, построить потенциальную диаграмму. Схема характеризуется следующими параметрами: E1 = 40 В, E3 = 30 В, R1 = 4 Ом, R2 = 16 Ом, R3 = 9 Ом, R4 = 8 Ом, R5 = 3 Ом, R6 = 6 Ом, Ri1 = 1 Ом, Ri3 = 1 Ом.
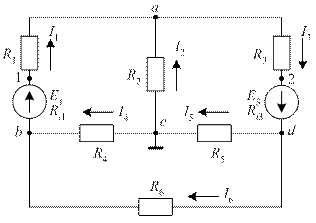
Рис. 28. К примеру расчета методом узловых потенциалов
Решение
Задаемся положительными направлениями токов в ветвях схемы. Заземляем узел c, и приравниваем его потенциал нулю. Определяем проводимости ветвей схемы:
g1= 1/(R1 + Ri1) = 1/(4 + 1) = 0,2 См; g2= 1/R2 =1/16 = 0,0625 См;
g3= 1/(R3 + Ri3) = 1/(9 + 1) = 0,1 См; g4= 1/R4 = 1/8 = 0,125;
g5= 1/R5= 1/3 = 0,3333; g6= 1/R6= 1/6 =0,1667.
Определяем собственные и смежные проводимости узлов:
gaa = g1 + g2 + g3 = 0,2 + 0,0625 + 0,1 = 0,3625 См;
gbb = g1 + g4 + g6 = 0,2 + 0,125 + 0,1667 = 0,4917 См;
gdd = g3 + g5 + g6 = 0,1 + 0,3333 + 0,1667 = 0,6 См;
gab = gba = – g1 = – 0,2 См; gad = gda = – g3 = – 0,1 См;
gbd = gdb = – g6 = – 0,1667 См.
Составляем систему уравнений метода узловых потенциалов:
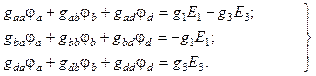
Подставляем в нее численные значения:
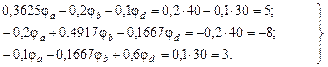
Выполним решение этой линейной алгебраической системы уравнений относительно потенциалов узлов с помощью определителей, причем в отличие от примера 1 рассчитаем дополнительные определители Δa, Δb, Δd непосредственно (без вычисления алгебраических дополнений):
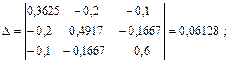
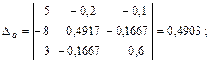
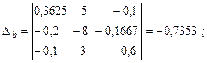
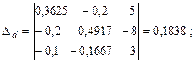
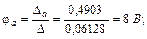
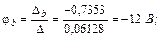
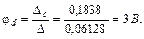
С помощью закона Ома для участка цепи с источником ЭДС определяем токи ветвей:
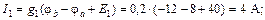
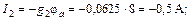
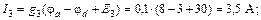
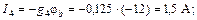
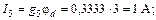
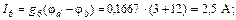
Вычисляем напряжения на зажимах источников:
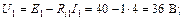
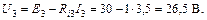
Построим потенциальную диаграмму (рис. 29) для контура cbadc.
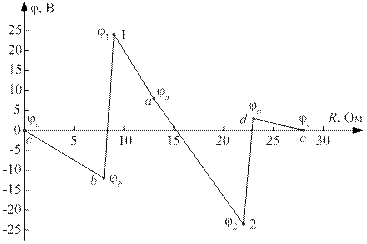
Рис. 29. Потенциальная диаграмма для контура cbadc
Начнем построение из узла c, потенциал которого равен нулю. Потенциалы узлов b, a, d найдены ранее в процессе расчета. Потенциалы промежуточных точек 1 и 2 равны:
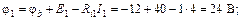
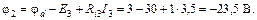
Как видим, при переходе через источник в направлении увеличения ЭДС потенциал возрастает, а при переходе в обратном направлении – убывает.
На потенциальной диаграмме по оси абсцисс откладываем сопротивления соответствующих участков, по оси ординат – потенциалы узлов. Узел c на потенциальной диаграмме расположится в начале координат. Из начала координат по оси абсцисс откладываем в масштабе сопротивление R4 = 8 Ом, а по оси ординат – потенциал φb = –12 В. Из концов соответствующих точек восстанавливаем перпендикуляры к осям, и на их пересечении получаем точку b. Точки c и b на потенциальной диаграмме соединяем отрезком прямой. Далее по оси абсцисс откладываем внутреннее сопротивление первого источника Ri1 = 1 Ом, добавляя его к сопротивлению четвертой ветви, а по оси ординат откладываем из начала координат потенциал φ1 = 24 В. Получаем точку 1. Соединяем ее отрезком прямой с точкой b. Затем по оси абсцисс откладываем сопротивление R1 = 4 Ом, а по оси ординат – потенциал φa = 8 Ом. Получаем точку a. И т.д. до узла c.
Сравним потенциальную диаграмму рис. 29 для замкнутого контура схемы рис. 28 с потенциальной диаграммой рис. 6 для участка электрической цепи, изображенного на рис. 5. Как видим, потенциальная диаграмма рис. 29 замкнутая, а рис. 6 не замкнутая. Кроме того, наклоны отрезков прямых на участках с пассивными элементами на рис. 6 одинаковы, поскольку на участке электрической цепи через все эти элементы течет один и тот же ток. На рис. 29 наклон отрезков прямых на участках с пассивными элементами различен, поскольку эти элементы принадлежат разным ветвям и через них текут разные токи. В схеме рис. 5 источники идеальные. На рис. 6 им соответствуют вертикальные отрезки прямых. В схеме рис. 28 источники реальные. На рис. 29 им соответствуют отрезки прямых b1 и 2d, наклон которых обусловлен наличием внутренних сопротивлений источников.
Метод двух узлов
В электротехнической практике часто встречаются схемы, содержащие только два узла. Для расчета таких схем специально создан метод, получивший название метода двух узлов. Этот метод по существу является частным случаем метода узловых потенциалов.
На рис. 30 приведена обобщенная схема электрической цепи постоянного тока с двумя узлами a и b. Схема состоит из m ветвей, часть или все из которых содержат источники ЭДС. В общем случае в некоторых ветвях могут быть и источники тока.
В методе двух узлов за искомое принимают напряжение Uab между узлами a и b схемы. Если при этом один из двух узлов, например, узел b заземлить и принять его потенциал равным нулю (φb = 0), то потенциал φa второго узла будет равен напряжению Uab.
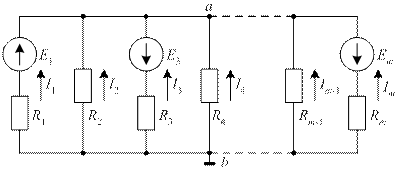
Рис. 30. К методу двух узлов
Воспользуемся методом узловых потенциалов и составим уравнение относительно потенциала φa:
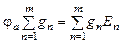 .
.
Решая это уравнение относительно Uab = φa, получаем:
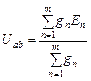 ,
,
где в числителе берется алгебраическая сумма произведений проводимостей gn = 1/Rn и ЭДС En для ветвей, содержащих источники ЭДС. (Для ветвей без источников произведение gnEn обращается в ноль). Члены суммы берутся со знаком плюс, если стрелка источника ЭДС направлена к узлу a, и со знаком минус, если стрелка направлена от узла a. При наличии в части ветвей схемы идеальных источников тока алгебраическая сумма произведений gnEn будет содержать также токи идеальных источников тока Ik. Выбор знака для источника тока такой же, как и для источника ЭДС. Знаменатель формулы Uab представляет собой арифметическую сумму проводимостей всех ветвей схемы. Причем в этой сумме проводимости ветвей, содержащих идеальные источники тока, равны нулю, т.к. внутреннее сопротивление источника тока равно бесконечности.
После того, как напряжение Uab между двумя узлами найдено, можно определить ток в любой ветви схемы по формуле закона Ома для участка цепи с источником ЭДС
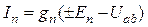 ,
,
где знак ЭДС выбирается исходя из направления ЭДС в n–й ветви.
Метод наложения
Метод наложения является следствием общефизического принципа наложения (суперпозиции), согласно которому реакция цепи на сумму отдельных воздействий равна сумме реакций цепи на каждое воздействие в отдельности.
В электротехнической практике в качестве воздействий чаще всего выступают ЭДС, а в качестве реакций – токи.
Для обоснования применения принципа наложения к анализу электрической цепи можно использовать формулу (10). В этой формуле отношение Δpq/Δ имеет размерность проводимости (См), а текущий член суммы 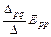 , являющийся произведением проводимости на контурную ЭДС, имеет размерность тока (А) и представляет собой реакцию цепи (частичный ток q-го контура) на контурную ЭДС Epp p-го контура. Поэтому в соответствии с формулой (10) контурный ток равен сумме частичных контурных токов от действия каждой контурной ЭДС в отдельности. Т.е. формула (10) является математическим выражением принципа наложения применительно к контурным токам.
, являющийся произведением проводимости на контурную ЭДС, имеет размерность тока (А) и представляет собой реакцию цепи (частичный ток q-го контура) на контурную ЭДС Epp p-го контура. Поэтому в соответствии с формулой (10) контурный ток равен сумме частичных контурных токов от действия каждой контурной ЭДС в отдельности. Т.е. формула (10) является математическим выражением принципа наложения применительно к контурным токам.
Согласно методу контурных токов контурные ЭДС представляют собой алгебраические суммы ЭДС источников, действующих в рассматриваемом контуре. Токи ветвей являются алгебраическими суммами контурных токов. Поэтому принцип наложения применим и к токам ветвей. А именно: токи ветвей можно рассматривать как алгебраические суммы частичных токов этих же ветвей от поочередного действия каждого из источников электрической энергии в отдельности:
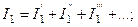
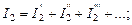
…………………,
где токи с одним, двумя и т.д. штрихами (число штрихов последнего члена каждой суммы равно количеству источников в схеме) – это так называемые частичные токи ветвей.
Методика расчета по методу наложения.
Расчет состоит из f + 1 этапов, где f – количество источников в схеме.
На первом этапе в цепи оставляют только один источник ЭДС или тока. Для остальных источников ЭДС и тока полагают E = 0, Ik = 0 и оставляют только их внутренние сопротивления Ri или проводимости gi. При этом ветви с идеальными источниками тока разрывают, а ветви с идеальными источниками напряжения заменяют короткозамкнутыми перемычками между точками их включения. Далее любым методом (чаще всего с помощью закона Ома) определяют частичные токи I' во всех ветвях схемы от действия оставленного источника. Выбранные условные положительные направления частичных токов в ветвях на схеме обозначают стрелками.
На втором этапе оставляют в цепи второй источник и аналогичным образом определяют частичные токи I" во всех ветвях схемы от действия второго источника, также обозначая на схеме направления действия частичных токов I" стрелками.
И т.д., выполняя на каждом новом этапе расчет частичных токов от действия очередного источника ЭДС или тока.
На последнем этапе определяют токи ветвей как алгебраические суммы частичных токов (с учетом направлений частичных токов в ветвях).
Примечание. Расчет мощностей и энергий можно вести только по полным токам ветвей, т.к. мощности и энергии являются квадратичными функциями токов.
Пример 3. Рассчитать токи в ветвях схемы рис. 31 методом наложения. Схема характеризуется следующими параметрами: E4 = 40 В, E6 = 32 В, Ri4 = 1 Ом, Ri6 = 1 Ом, R1 = 6 Ом, R2 = 10 Ом, R3 = 2 Ом, R4 = 7 Ом, R5 = 8 Ом, R6 = 9 Ом.
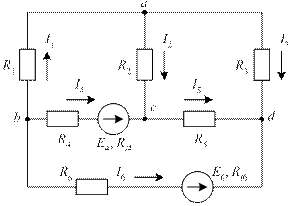
Рис. 31. К методу наложения
Решение
Анализируемая схема является мостовой. В схеме четыре узла и шесть ветвей. В четвертой и шестой ветвях имеются источники с ЭДС E4, E6 и внутренними сопротивлениями источников Ri4, Ri6. Выбранные положительные направления токов ветвей указаны на схеме стрелками.
Расчет токов в рассматриваемой схеме методом наложения необходимо выполнять в три этапа. На первом этапе рассчитаем частичные токи ветвей I' от действия источника в шестой ветви. На втором этапе определим частичные токи ветвей I" от действия источника в четвертой ветви. На третьем этапе найдем результирующие токи ветвей.
Первый этап.Удаляем из схемы ЭДС E4, оставив в схеме внутреннее сопротивление Ri4. Схема приобретает вид, изображенный на рис. 32.
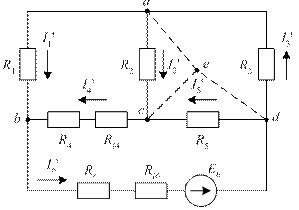
Рис. 32. К первому этапу метода наложения
Заменим контур-треугольник acd эквивалентной звездой (на схеме рис. 32 лучи звезды показаны внутри контура acd пунктиром). Схема приобретает вид, изображенный на рис. 33.
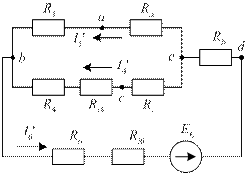
Рис. 33. Схема замещения для первого этапа метода наложения
Для расчета сопротивлений эквивалентной звезды воспользуемся формулами (7):
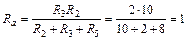 Ом;
Ом; 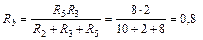 Ом;
Ом;
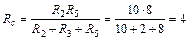 Ом.
Ом.
Схема рис. 33 по структуре соединения ветвей аналогична схеме рис. 16 и представляет собой смешанное соединение в цепи постоянного тока. На схеме рис. 33 первая и четвертая ветви включены параллельно, а шестая ветвь включена последовательно с ними. Определим эквивалентные сопротивления каждой ветви схемы рис. 33.
Первая ветвь
R1a = R1 + Ra = 6 + 1 = 7 Ом.
Четвертая ветвь
R4c = R4 + Ri4 + Rc = 7 + 1 + 4 = 12 Ом.
Шестая ветвь
R6b = R6 + Ri6 + Rb = 9 + 1 + 0,8 = 10,8 Ом.
Применяя формулу (6) для смешанного соединения в цепи постоянного тока, находим входное сопротивление схемы по отношению к ЭДС E6 схемы рис. 33:
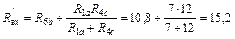 Ом.
Ом.
Далее по закону Ома находим частичный ток шестой ветви
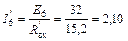 А.
А.
Для определения частичных токов первой и четвертой ветвей рассчитаем напряжение между узлами e и b схемы рис. 33:
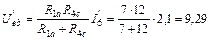 В.
В.
Частичные токи первой и четвертой ветвей находим по закону Ома:
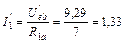 А;
А; 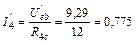 А.
А.
Для нахождения частичных токов второй, третьей и пятой ветвей схемы рис. 32 необходимо рассчитать напряжения 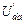 ,
, 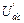 ,
, 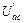 . Расчет выполняем, используя схему рис. 33:
. Расчет выполняем, используя схему рис. 33:
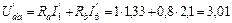 В;
В; 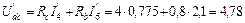 В;
В;
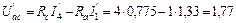 В.
В.
Возвращаемся к схеме рис. 32 и, используя закон Ома для участка цепи, определяем частичные токи второй, третьей и пятой ветвей:
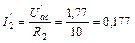 А;
А; 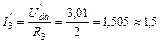 А;
А; 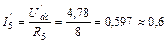 А.
А.
Второй этап. Удалим из исходной схемы (см. рис. 31) ЭДС E6, оставив в схеме внутреннее сопротивление Ri6. Схема приобретает вид, изображенный на рис. 34.
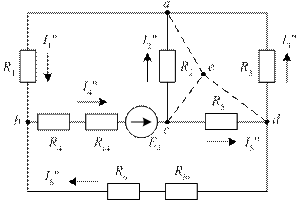
Рис. 34. Ко второму этапу метода наложения
Заменим контур-треугольник acd эквивалентной звездой (на схеме рис. 34 лучи звезды показаны внутри контура acd пунктиром). Схема приобретает вид, изображенный на рис. 35.
Схема рис. 35 – это смешанное соединение в цепи постоянного тока. Численные значения сопротивлений Ra, Rb, Rc эквивалентной звезды схемы рис. 35 те же, что и схемы рис. 33, а именно: Ra = 1 Ом, Rb = 0,8 Ом, Rc = 4 Ом. Поэтому и эквивалентные сопротивления каждой ветви схемы рис. 35 такие же, как и у и схемы рис. 33. Эти сопротивления найдены выше: R1a = = 7 Ом, R4c = 12 Ом, R6b = 10,8 Ом.
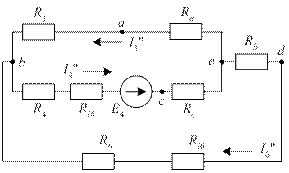
Рис. 35. Схема замещения для второго этапа метода наложения
На схеме рис. 35 первая и шестая ветви включены параллельно, а четвертая ветвь включена последовательно с ними. Применяя формулу (6) для смешанного соединения в цепи постоянного тока, находим входное сопротивление по отношению к ЭДС E4 схемы рис. 35:
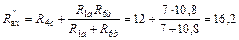 Ом.
Ом.
Далее по закону Ома находим частичный ток четвертой ветви
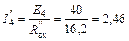 А.
А.
Для определения частичных токов первой и шестой ветвей рассчитаем напряжение между узлами e и b схемы рис. 35:
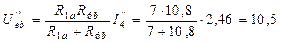 В.
В.
Частичные токи первой и шестой ветвей находим по закону Ома:
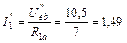 А;
А; 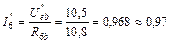 А.
А.
Для нахождения частичных токов второй, третьей и пятой ветвей схемы рис. 34 необходимо рассчитать напряжения 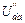 ,
, 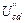 ,
, 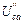 . Расчет выполняем, используя схему рис. 35:
. Расчет выполняем, используя схему рис. 35:
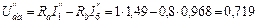 В;
В; 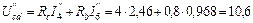 В;
В;
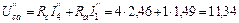 В.
В.
Возвращаемся к схеме рис. 34 и, используя закон Ома для участка цепи, определяем частичные токи второй, третьей и пятой ветвей:
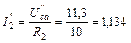 А;
А; 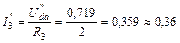 А;
А; 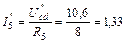 А.
А.
Третий этап. Токи ветвей схемы рис. 31 определяем как алгебраические суммы частичных токов:
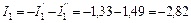 А;
А; 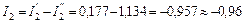 А;
А;
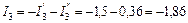 А;
А; 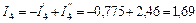 А;
А;
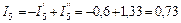 А;
А; 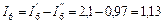 А.
А.
Принцип взаимности
Линейные электрические цепи обладают принципом взаимности. Этот принцип можно сформулировать применительно к источнику ЭДС или тока. Сформулируем этот принцип применительно к источнику ЭДС.
На рис. 36 изображены две схемы электрической цепи, в каждой из которых выделены по две ветви q и p. В каждой схеме имеется только один источник ЭДС. На рис. 36, а источник ЭДС расположен в ветви q, а на рис. 36, б аналогичный источник находится в ветви p. Оставшаяся часть схемы может иметь произвольную структуру, важно, что эта структура для обоих рисунков одинакова.
а) 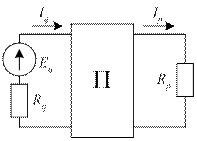 б)
б) 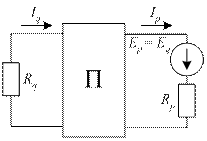
Рис. 36. Схемы с источником ЭДС в ветви q (а) и ветви p (б)
Принцип взаимности формулируется следующим образом.
В любой сколь угодно сложной линейной электрической цепи ток в ветви p, созданный ЭДС Eq, находящейся в ветви q (рис. 36 а) будет равен току Iq в ветви q, созданному ЭДС Ep = Eq, находящейся в p-й ветви (рис. 36 б).
Для доказательства принципа взаимности воспользуемся методом контурных токов, и выберем независимые контура так, чтобы ветви q и p являлись внешними ветви (хордами). Тогда токи этих ветвей будут совпадать с контурными токами. С учетом этого из формулы (10) для схемы рис. 36 а получаем:
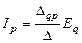 .
.
Аналогичным образом для схемы рис. 36 б имеем:
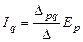 .
.
В этих двух выраженияхEp = Eq, Δpq = Δqp. Следовательно, Ip = Iq и принцип взаимности доказан.
Из последних двух соотношений имеем также:
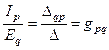 и
и 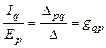 .
.
Проводимость gpq = gqpназывается взаимной или передаточной проводимостью ветвей q и p. Взаимная проводимость двух ветвей определяется как отношение тока одной ветви к ЭДС другой ветви.
Если в последних двух соотношениях рассматривать ток и ЭДС применительно к одной ветви q или p, то получим:
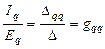 или
или 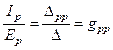 .
.
Проводимости gqq и gpp называются входными проводимостями ветвей q и p. Входная проводимость ветви представляет собой отношение тока ветви, содержащей единственный в схеме источник ЭДС, к величине ЭДС.
Величина, обратная входной проводимости, называется входным сопротивлением ветви:
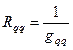 или
или 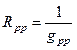 .
.
Аналогичным образом взаимное сопротивление двух ветвей определится как
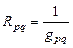 или
или 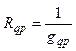 .
.
Дата добавления: 2016-06-29; просмотров: 6252;











