Принцип компенсации

Принцип компенсации формулируется следующим образом.

Токи в электрической цепи не изменятся, если ветвь (или часть ветви) с сопротивлением R и током I заменить ЭДС E, равной по величине падению напряжения в данной ветви RI и направленной навстречу току этой ветви.

Принцип компенсации иллюстрируется схемами, представленными на рис. 37а, б. Эти же схемы можно использовать для доказательства принципа компенсации.

а) б)

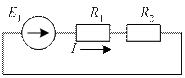
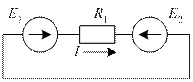
Рис. 37. К принципу компенсации: а) исходная схема; б) схема замещения

На рис. 37а имеем одноконтурную схему с одним источником ЭДС и двумя сопротивлениями. Для этой схемы справедливо следующее уравнение второго закона Кирхгофа:

.

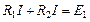Это линейное алгебраическое уравнение. Любое его слагаемое можно перенести из одной части уравнения в другую, заменив знак на противоположный. Перенесем в правую часть R₂I. В правой части наряду с ЭДС E₁ появится еще одно слагаемое, которое можно рассматривать как дополнительную ЭДС E₂ = – R₂I:

.

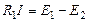Последнему уравнению соответствует схема рис. 37б, иллюстрирующая принцип компенсации.

Подобную операцию по переносу слагаемых из левой части уравнения второго закона Кирхгофа в правую можно осуществить и для разветвленной цепи, поэтому принцип компенсации применим и к разветвленным электрическим цепям.

Следует отметить, что ЭДС источника, компенсирующего собой напряжение на участке цепи, определяется для конкретного тока участка. Если ток рассматриваемого участка цепи изменился вследствие изменения параметров остальной части цепи, то изменится и ЭДС компенсирующего источника. Поэтому такой источник является зависимым.