Действия над комплексными числами в тригонометрической форме

Тригонометрическая форма записи комплексных чисел является очень удобной при умножении и делении чисел.

Возьмем два числа в тригонометрической форме:

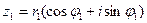
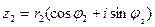
1) Произведением двух комплексных чисел называется число, модуль которого равен произведению модулей этих чисел, а аргумент равен сумме аргументов данных комплексных чисел.

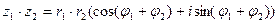(8)

2) Частным двух комплексных чисел называется число, модуль которого равен частному модулей этих чисел, а аргумент равен разности аргументов данных комплексных чисел.

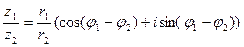(9)

3) При возведении комплексного числа в степень с натуральным показателем нужно возвести в степень его модуль, а аргумент умножить на показатель степени.

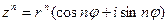(10)

Формула (10) называется формулой Муавра.

4) Чтобы извлечь корень п-й степени из комплексного числа, нужно извлечь корень из модуля этого числа, а аргумент поделить на показатель корня.

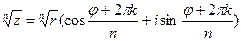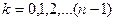, (11)

Задания для закрепления и самоконтроля:

1. Найти произведение комплексных чисел:

,

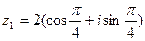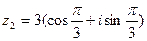. Ответ: .

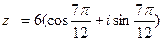2. Найти частное комплексных чисел:

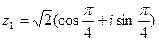
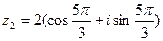. Ответ: .

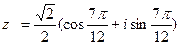3. Вычислить: .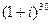

Ответ: .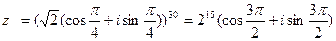

4. Найти .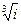

Примечание: сначала переведите данное число в тригонометрическую форму, а потом по формуле (11) извлеките корень, выбрав k=0,1,2.

Ответ: ,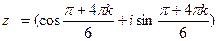

, ,

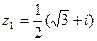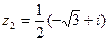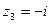
Контрольные вопросы.

1. Что называется модулем комплексного числа?

2. Что называется аргументом комплексного числа?

3. Как вычислить модуль и аргумент комплексного числа?

4. Почему аргумент не определяется однозначно для любого комплексного числа?

5.Как найти произведение двух комплексных чисел в тригонометрической форме?

6. Как найти частное двух комплексных чисел в тригонометрической форме?

7. Как возвести комплексное число в натуральную степень?

8. Как извлечь корень из комплексного числа?

9. Сколько результатов получаем при извлечении корня из комплексного числа, заданного в тригонометрической форме?

Литература:

И.И.Валуцэ, Г.Д.Дилигул «Математика для техникумов», М.,1989, с.101-110.